一元二次不等式恒成立问题探究

江西省赣州市兴国县第三中学 刘松柏

一元二次不等式恒成立问题探究

江西省赣州市兴国县第三中学 刘松柏

一元二次不等式与其对应的函数与方程之间存在着密切的联系。在解决具体的数学问题时，要注意三者之间的相互联系，并在一定条件下相互转换。我们首先看一元二次不等式恒成立的条件：

（1） 不 等 式 ax2+bx+c＞0 对 任 意 实 数 x 恒 成 立或

（2）不等式 ax2+bx+c＜0 对 任意实数 x 恒成立或次不等式恒成立问题，常根据二次函数图象与x轴的交点情况确定判别式的符号，进而求出参数的取值范围。归纳起来常见的命题角度有：

（1）形如 f（x）≥ 0（x ∈ R）确定参数的范围；

（2）形如 f（x）≥ 0（x ∈ [a，b]）确定参数范围；

（3）形如 f（x）≥ 0（参数 m ∈ [a，b]）确定 x 的范围。

角度一：形如 f（x）≥ 0（x ∈ R）确定参数的范围

例 1 已知不等式 mx2-2x-m+1 ＜ 0，是否存在实数 m 对所有的实数x，不等式恒成立？若存在，求出m的取值范围；若不存在，请说明理由。

解：不等式 mx2-2x-m+1 ＜ 0 恒成立，

即函数 f（x）=mx2-2x-m+1 的图象全部在 x 轴下方。

当 m ≠ 0 时，函数 f（x）=mx2-2x-m+1 为二次函数，

需满足开口向下且方程 mx2-2x-m+1=0 无解，

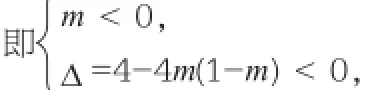
此不等式组的解集为空集，即m无解。

综上可知，不存在这样的实数m。

例 2 设函数 f（x）=mx2-mx-1（m ≠ 0），若对于 x ∈ [1,3]，f（x）＜ -m+5 恒成立，求 m 的取值范围。

解：要使 f（x）＜ -m+5 在 [1,3] 上恒成立，

则 mx2-mx+m-6 ＜ 0，即在 x ∈ [1,3]上恒成立。

有以下两种方法：

当 m ＞ 0 时，g（x）在 [1,3]上是增函数，所以 g（x）max=g（3）＝ 7m-6 ＜ 0。

所以 m ＜ 6。所以 m ＜ 0。

法二：因为

角度三：形如 f（x）≥ 0（参数 m ∈ [a，b]）确定 x 的范围

例 3 对任意 m ∈ [-1,1]，函数 f（x）＝ x2+（m-4）x+4-2m 的值恒大于零，求 x的取值范围。

解：由 f（x）=x2+（m-4）x+4-2m

=（x-2）m+x2-4x+4，

令 g（m）=（x-2）m+x2-4x+4。

由题意知在 [-1,1]上，g（m）的值恒大于零，

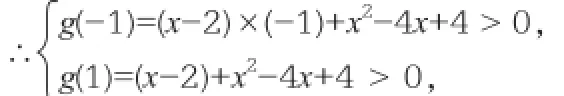
解得 x＜1 或 x＞3。

故当 x＜1 或 x＞3 时，对任意的 m ∈ [-1,1]，函数 f（x）的值恒大于零。

总之，解决恒成立问题注意下面两点就可以了：

（1）解决恒成立问题一定要清楚选谁为主元，谁是参数。一般地，知道谁的范围，就选谁当主元，求谁的范围，谁就是参数。

（2）对于二次不等式恒成立问题，恒大于0就是相应的二次函数的图象在给定的区间上全部在 x轴上方；恒小于0就是相应的二次函数的图象在给定的区间上全部在x轴下方。