基于改进灰色关联-TOPSIS模型的乌鲁木齐市水资源脆弱性评价
魏光辉(新疆塔里木河流域管理局,新疆 库尔勒 841000)
基于改进灰色关联-TOPSIS模型的乌鲁木齐市水资源脆弱性评价
魏光辉
(新疆塔里木河流域管理局,新疆 库尔勒 841000)
乌鲁木齐市水资源脆弱性评价指标体系,由社会发展系统、水资源系统和生态环境系统3个子系统、8项指标组成,将水资源脆弱性划分为高中低5类.采用灰色关联-TOPSIS模型对不同时期水资源脆弱性进行评价,结果表明:人均用水量、地下水源供水率、中水回用率与有效灌溉面积率这4项指标是影响研究区水资源脆弱性的主要因素,2005—2015年研究区水资源脆弱性呈现显著加重趋势.
水资源;脆弱性评价;灰色关联分析法;TOPSIS模型;乌鲁木齐市
0 引 言
水资源在人类经济和社会可持续发展中占有非常重要的地位[1-3].随着当前社会经济的不断发展,其对水资源的依赖性日益增加[4].受气候变化对水资源的影响,我国的水资源安全也逐渐受到威胁[5-6].水资源脆弱性(Water Resources Vulnerability,简称WRV)是评价水资源安全的重要标准,作为制约水资源安全的关键问题,水资源脆弱性研究日益受到国内外学者们的普遍关注[7-8].开展水资源脆弱性研究对预测未来水资源安全变化趋势,探求水资源安全的关键要素和过程具有重要意义[8-9].
1 水资源脆弱性评价指标体系构建
乌鲁木齐市水资源脆弱性评价体系包括3个方面、8项指标.3个方面包括社会发展系统、水资源系统和生态环境系统.其中社会发展系统包括人均GDP(C1,万元·人-1)与人均用水量(C2,m3·人-1)2项指标;水资源系统包括人均水资源量(C3,m3)、地下水源供水率(C4,%)、中水回用率(C5,%)、供水模数(C6,万m3·km-2)与有效灌溉面积率(C7,%)这5项指标;生态环境系统包括生态环境用水率(C8,%)这1项指标.研究区水资源脆弱性评价指标体系(见表1).
表1中指标性质一栏,所谓正指标,是指该指标值越大则表明相应的水资源脆弱性越轻微;反之,所谓负指标,是指该指标值越小则表明相应的水资源脆弱性越轻微.将表1中8个评价指标划分为5个等级,其中Ⅰ级表示水资源不脆弱,Ⅱ级表示水资源轻度脆弱,Ⅲ级表示水资源中等脆弱,Ⅳ级表示水资源比较脆弱,Ⅴ级表示水资源严重脆弱.各指标等级划分(见表2).
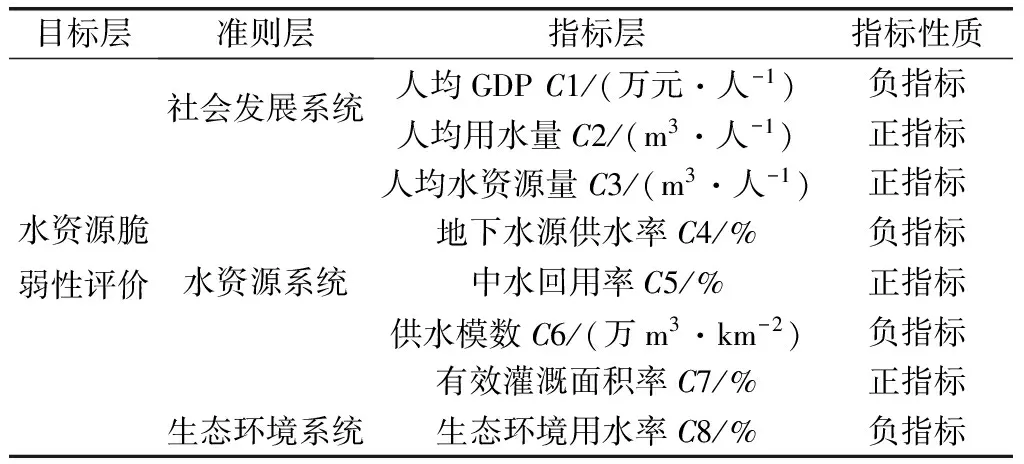
表1 水资源脆弱性评价指标体系
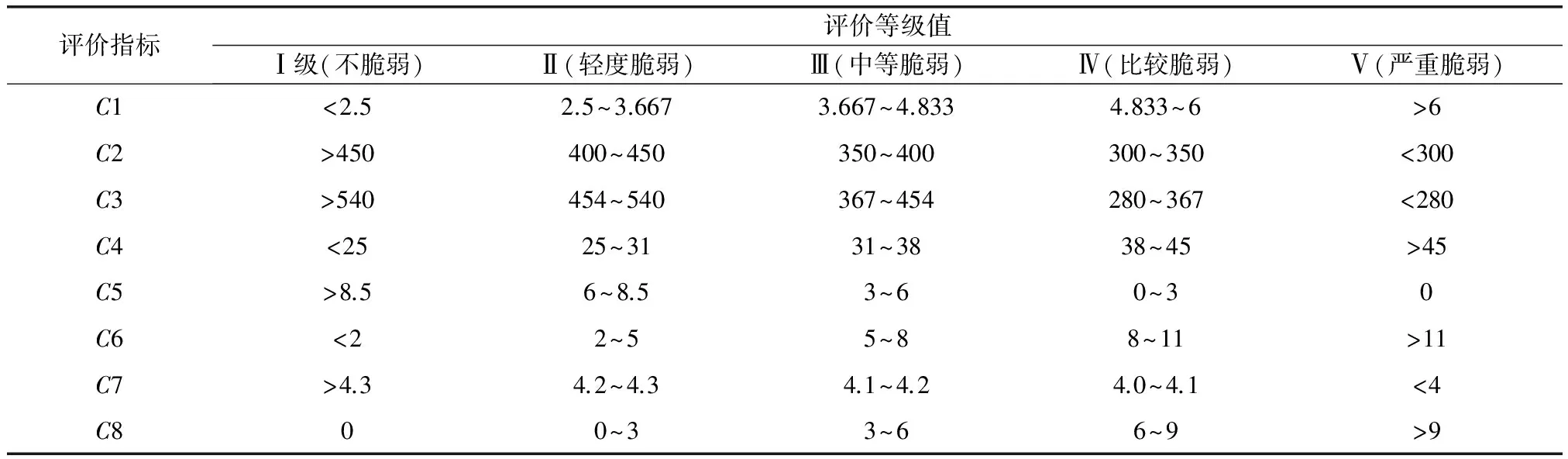
表2 乌鲁木齐市水资源脆弱性评价等级标准
2 评价指标权重确定
2.1 G1法确定指标主观权重
2.1.1 计算原理
专家在对不同的指标x1和x2进行价值判断时,可判定x1优于x2或x2优于x1,或既非x1优于x2,也非x2优于x1,这种直觉判断被称之为偏好,采用符号“>”、“<”和“·”分别表示“优于”、“劣于”和“无差异”的关系.
假设评估问题中包括n个经过归一化的评价指标:x1,x2,…,xn,专家根据自身工作经验和一定准则将这些指标按其重要性排序:
x1>x2>…>xn
(1)
相邻指标的重要性程度比用公式表示为:
wp-1/wp=rp(p=2,3,…,n)
(2)
式中:wp为指标xp的权重;rp取值为1.0,1.2,1.4,1.6,1.8,分别表示指标xp-1与xp相比为同样重要、略微重要、明显重要、非常重要和极重要.[10]
2.1.2 计算步骤
若指标x1,x2,…,xn具有x1>x2>…>xn的序关系,满足rp-1>1/rp(p=2,3,…,n),则各指标权重为:
(3)
wp-1=wp·rp(p=n,n-1,2)
(4)
由此可以依次计算出各指标权重.
2.2 熵值法求解指标客观权重
熵值法是利用指标实际值所提供的信息量大小来确定指标的客观权重,具有精度高、客观性强的特点,其计算步骤如下:
(1)将指标矩阵归一化处理:
(5)
式中:xmax、xmin分别为不同方案同一指标下的最优、最劣值.
(2)根据熵的定义,m个方案n个评价指标,可以确定评价指标的熵为:
(6)
为使1nfij有意义,需对fij加以修正,修正式如下:
(7)
计算评价指标的熵权W:
(8)
2.3 博弈论法确定指标综合权重
为使评价指标权重更具科学性和客观性,可用L种方法对各指标赋权,构造评价指标权重集uk={uk1,uk2,…,ukm},k=1,2,…,L,记这L个不同向量间的任意线性组合为:
(9)
式中:u—权重集的一种可能的权重向量.
基于博弈论思想,优化这L个不同的线性组合系数αk,使之达到极小化u与各个uk之间离差的效果,此时可得对策模型为:
(10)
对式(10)进行最优化一阶导数,可得:
(11)
运用Matlab计算求得(α1,α2,…,αl),将其归一化处理:
(12)
即得评价指标综合权重:
(13)
3 灰色关联-TOPSIS综合评价模型
灰色关联-TOPSIS模型计算步骤如下:
(1)根据式(5)与式(13)计算评价模型的加权标准化矩阵,并计算此时评价方案集合的理想解和负理想解;
(2)根据所得加权标准化矩阵,利用灰色关联理论计算各评价指标与理想解、负理想解的灰色关联系数,并构建灰色关联系数矩阵;
(3)运用TOPSIS模型思路,以步骤(2)所得灰色关联系数矩阵为基础,再次确定矩阵正、负理想解,分别计算各评估对象到理想解和负理想解的距离,并计算其相对贴近度;
(4)根据相对贴近度大小,对不同年份水资源脆弱性进行排序并确定其等级范围.
灰色关联-TOPSIS模型的具体计算过程可参见文献[11].
4 模型应用
4.1 研究区概况和数据来源
乌鲁木齐市地处西北内陆干旱区,降雨稀少、蒸发强烈,人均水资源量为340m3,属于极度缺水城市之一(国际公认绝对缺水水资源占有标准量为500m3).截止到2014年底,乌鲁木齐市全年实现国内生产总值2 510亿元.其中,第一产业实现增加值30亿元,第二产业实现增加值955亿元,第三产业实现增加值1 525亿元;三次产业结构比例为1.2 ∶38.1 ∶60.7.全年农作物播种面积92 446.67ha,其中粮食播种面积1 995.333ha,棉花播种面积1 500ha,油料播种面积3 573.33ha,蔬菜(含薯类)播种面积23 993.33ha.年末全市常住人口为353万人,城镇居民人均可支配收入23 755元,农牧民人均纯收入13 335元.本文指标数据主要来自2005—2011年乌鲁木齐市水资源公报和同期乌鲁木齐市国民经济和社会发展统计公报,2015年和2020年数据来自乌鲁木齐市城市总体规划(2009—2020年),不同年份水资源脆弱性指标值(见表3).
根据表2数据,确定水资源脆弱性评价指标等级临界值(见表4).
4.2 水资源脆弱性评价
(1)评价指标标准化
根据评价指标性质,利用式(5)对表3与表4中的数据进行标准化处理,结果(见表5).
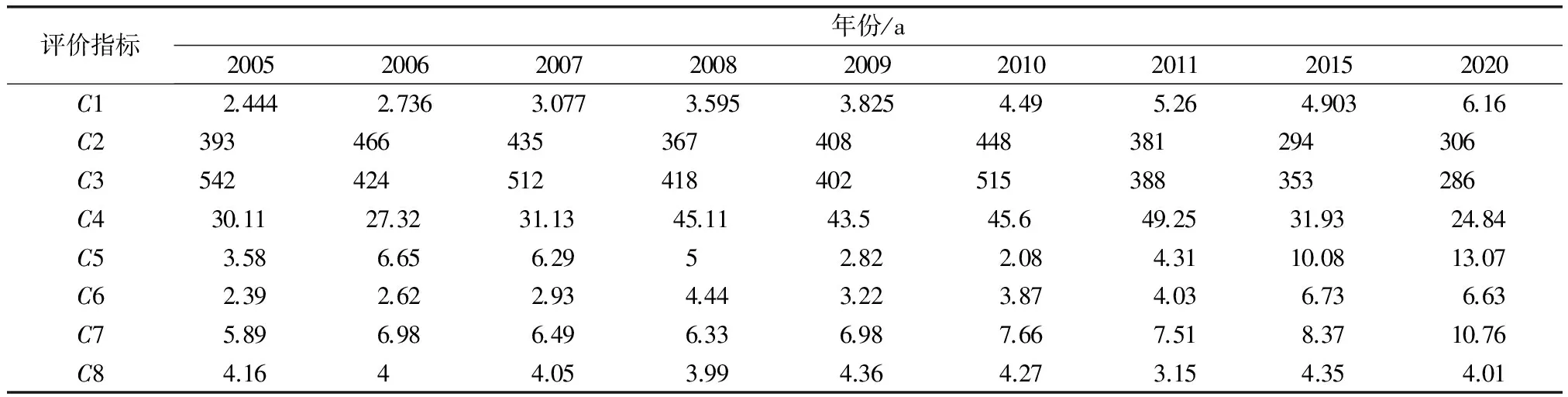
表3 乌鲁木齐市不同年份水资源脆弱性指标值

表4 水资源脆弱性评价等级临界值
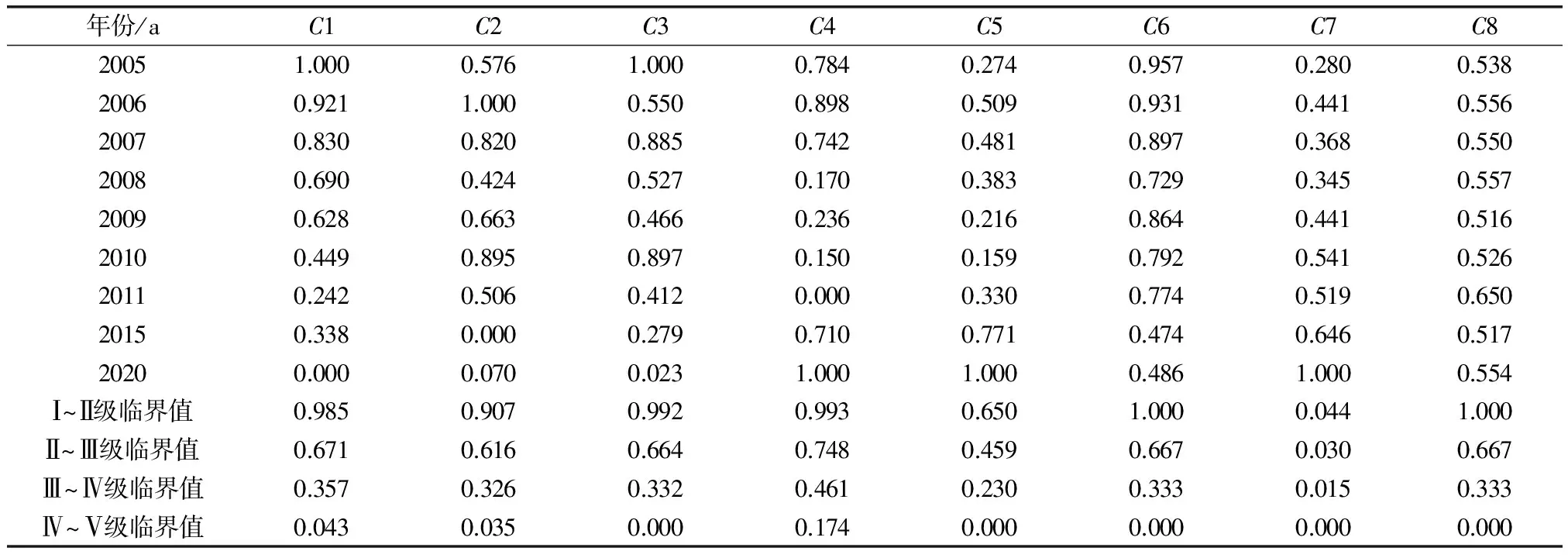
表5 评价指标归一化矩阵
(2)确定评价指标综合权重
根据表3与表4数据,利用式(5)~式(8)计算各评价指标的熵权,得到βj=(0.127 9,0.134 0,0.129 1,0.135 8,0.133 1,0.087 4,0.168 2,0.084 5);利用式(1)~式(4)计算各评价指标的主观权重wj=(0.125 6,0.138 0,0.128 1,0.141 6,0.136 0,0.058 7,0.217 2,0.054 8);根据博弈论理论,利用式(9)~式(13)计算各评价指标的综合权重,得uj=(0.126 4,0.135 8,0.128 8,0.137 7,0.134 8,0.067 3,0.194 7,0.074 5).
(3)贴近度计算及排序
将判断矩阵B=(bij)m×n与指标权重相乘,得加权决策矩阵.根据文献[11]计算步骤,计算其贴进度结果(见表6).
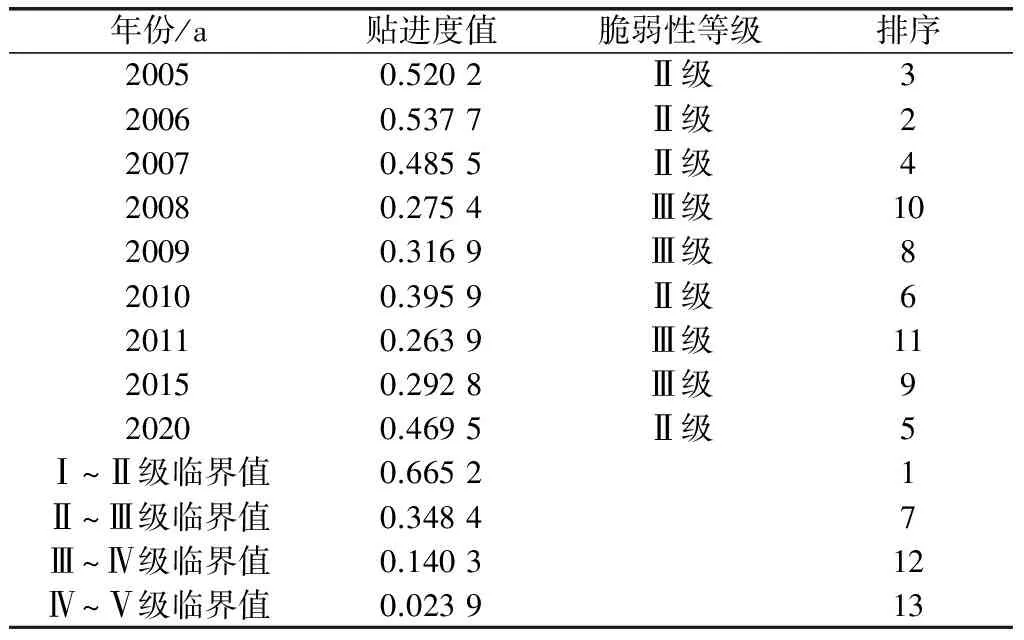
表6 不同年份水资源脆弱性贴进度及排序
4.3 结果分析
由表6计算结果可知:(1)2005—2015年乌鲁木齐市水资源脆弱性贴进度值呈现显著减小趋势,即水资源脆弱性呈现加重趋势;(2)研究区2006年的水资源脆弱性最轻微(贴进度值为0.537 7),2011年的水资源脆弱性最强(贴进度值为0.263 9),不同年份的水资源脆弱性优劣排序为2006年>2005年>2007年>2020年>2010年>2009年>2015年>2008年>2011年(“>”表示“优于”).
5 结 论
(1)博弈论法计算的评价指标权重表明:人均用水量、地下水源供水率、中水回用率与有效灌溉面积率这4项指标是影响研究区水资源脆弱性的主要因素.
(2)2005—2015年乌鲁木齐市水资源脆弱性呈现显著加重趋势,不同年份的水资源脆弱性优劣排序为:2006年>2005年>2007年>2020年>2010年>2009年>2015年>2008年>2011年(“>”表示“优于”).
(3)虽然目前我国尚未建立统一的水资源脆弱性评价体系,但下一步应从国内外研究成果出发,结合区域实际情况,建立具有普适性、科学性、全面性与合理性的水资源脆弱性综合评价体系.
[1] 李 倩,李 伦.基于PSR理论的河南省水资源脆弱性评价[J].河南城建学院学报,2015(4):48-53.
[2] 伏吉芮,瓦哈甫·哈力克.吐鲁番水资源脆弱性分析[J].黑龙江大学自然科学学报,2015(1):101-107.
[3] 姜海波,冯 斐,周 阳.塔里木河流域水资源脆弱性演变趋势及适应性对策研究[J].水资源与水工程学报,2014(2):81-84.
[4] 李玉芳,刘海隆,刘洪光.塔里木河流域水资源脆弱性评价[J].中国农村水利水电,2014(4):90-93.
[5] 翁建武,夏 军,陈俊旭.黄河上游水资源脆弱性评价研究[J].人民黄河,2013(9):15-20.
[6] 崔东文.基于改进BP神经网络模型的云南文山州水资源脆弱性综合评价[J].长江科学院院报,2013(3):1-7.
[7] 周念清,赵 露,沈新平.基于压力驱动模型评价长株潭地区水资源脆弱性[J].同济大学学报(自然科学版),2013(7):1061-1066.
[8] 胡蓓琳,潘争伟,金菊良.基于集对分析模型的巢湖流域水资源系统脆弱性评价[J].水电能源科学,2013(10):21-24.
[9] 马芳冰,王 烜,李春晖.水资源脆弱性评价研究进展[J].水资源与水工程学报,2012,(1):30-37.
[10] 费良军,王锦辉,王光社,等.基于改进熵权-G1-博弈论法的灌区运行状况综合评价[J].排灌机械工程学报,2015,33(10):895-900.
[11] 王锦辉,费良军,谢 芳,等.灰色关联理论-TOPSIS法的大型灌区运行状况综合评价[J].排灌机械工程学报,2015,33(11):985-990.
声 明
为适应我国信息化建设需要,扩大作者学术交流渠道和促进科技成果的迅速转化,本刊已加入“万方数据资源系统(ChinaInfo)数字化期刊群”、《中国学术期刊(光盘版)》和“中国期刊网”及中国“北极星”等网站或电子出版物,并成为其全文收录期刊和《中国学术期刊综合评价数据库》统计刊源.凡向本刊所投稿件,全体作者均视为愿意进入上述的数字化期刊群,并愿意将该论文的复制权、发行权、信息网络传播权、翻译权、汇编权等权利在全世界范围内转让给本刊.凡被录用的稿件,将同时通过因特网进行网络出版或提供信息服务,稿件一经刊用,其作者的著作权使用费由本刊一次性所发稿酬(即包括印刷版、光盘版和网络版各种使用方式的报酬)所包含.如有作者不同意上述事项,请在来稿时申明,本刊将作适当处理.
浙江水利水电学院学报编辑部
Evaluation of Water Resources Vulnerability in Urumqi Based on Improved Grey Relation-TOPSIS Model
WEI Guang-hui
(Tarim River Basin Administration of Xinjiang, Korla 841000, China)
Taking Urumqi City as an example, this paper has constructed water resources vulnerability evaluation index system, which is composed of 3 subsystems and 8 indicators, that is, the social development system, water resources system and ecological environment system, which divides the water resources vulnerability into 5 types. Using gray correlation-TOPSIS model to evaluate water resources vulnerability in different periods, the results show that: the main factors affecting water resources vulnerability in the study area are per capita water consumption, groundwater, water reuse rate and effective irrigation area. From 2005 to 2015, the water resource vulnerability in study area was significantly increased, and water resources vulnerability in different years were ranked as 2006>2005>2007>2020>2010>2009>2015>2008>2011.
water resources; vulnerability assessment; grey correlation analysis; TOPSIS model; Urumqi
2016-09-03
水利部公益性行业科研专项资助(201301102);
TV211.2
A
1008-536X(2017)02-0063-05
魏光辉(1981-),男,新疆石河子人,高级工程师,博士,主要从事干旱区水资源利用研究.
新疆水文学及水资源重点学科资助(XJSWSZYZDXK20101202)

