区域性夏季平均气温空间插值方法比较

汤伏全 李庚新

摘要使用ArcGIS软件，采用反距离权重法、普通克里格法和泛克里格法3种空间插值方法，以东北三省78个气象站点1999、2004年夏季平均气温数据为例进行了空间插值，并采用交叉检验的方法对插值结果进行了比较。结果表明，3种方法所得插值结果均能大致反映气温分布状况，但从精度分析上看，泛克里格法精度优于反距离权重法和普通克里格法。

关键词夏季；平均气温；空间插值；反距离权重法；普通克里格法；泛克里格法

中图分类号S161.2文献标识码

A文章编号0517-6611（2017）08-0191-04

Comparison of Spatial Interpolation Methods of Summer Average Temperature in Three Northeastern Provinces

TANG Fuquan，LI Gengxin（College of Geomatics，Xian University of Science and Technology，Xian，Shaanxi 710054）

AbstractUsing the ArcGIS software， three kinds of spatial interpolation methods， such as the inverse distance weight method（IDW）， the ordinary Kriging and the universal Kriging method， were used to interpolate the summer average temperature data of 78 meteorological stations in 1999 and 2004 in Northeast China.The cross test method compared the interpolation results.The results showed that the interpolated results of the three methods could reflect the temperature distribution， but from the point of view of accuracy analysis， the accuracy of the universal Kriging method was superior to IDW and the ordinary Kriging method.

Key wordsSummer；Average temperature；Spatial interpolation；Inverse distance weight；Ordinary Kriging method；Universal Kriging method

氣温是表示热量特征的重要参数，平均气温可以用来分析热量资源、进行自然区划和计算农业生产潜力[1]。然而由于经济、技术及人力等方面的原因，气象站点的数量是有限的，且分布不均匀，所以为了获得观测区气温空间分布规律，需要对相关气温数据进行空间插值。空间内插方法是研究区域变量空间分布的基本方法。近年来，随着GIS技术和地统计学的推广普及，实现气温数据栅格化的方法明显增多，如反距离权重法（IDW）、克里格插值法（Kriging）、样条插值法（Spline）、趋势面法（Trend）等，由于不同地区的地理条件、数据情况有所不同，不同的空间插值技术适用于不同的栅格化方法[2-5]。笔者以1999与2004年东北三省夏季平均气温数据作为研究对象，采用反距离权重法、普通克里格法、泛克里格法对研究区进行空间插值，并进行精度比较，评价各个方法在气温插值中的能力，以便于东北三省气温时空分布规律的研究。

1资料与方法

1.1研究区概况

东北地区处于欧亚大陆东岸，地形以山地、平原、河流为主，是我国纬度最高的区域，属于寒带大陆性季风气候，四季都是寒冰时期，气候季节性变化受东亚大气环流影响，气候变率较大，低温冷害等灾害性天气多发，山地面积众多，长白山、大小兴安岭是东北生态系统的重要天然屏障[6]。

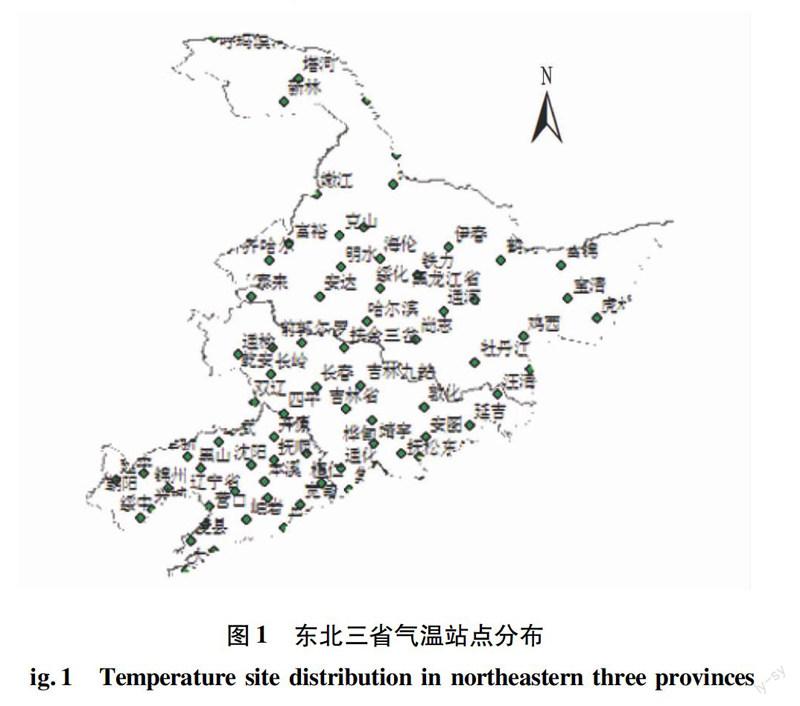
1.2数据来源原始资料为东北三省1954—2004年共78个气象站点（图1）日平均气温数据，站点地处119.7°～132.97° E、38.9°～52.97° N。由于原始数据庞杂，且许多年份夏季气温有所缺失或有明显的数据错误，为了减少因数据错误带来的影响和不必要的数据处理，根据所有数据的初步处理，选用了1999与2004年6、7、8月的日平均气温数据，利用Excel得到每个站点1999与2004年6、7、8月的平均气温作为每个站点的夏季平均气温。基础地理信息数据为国家基础地理信息中心提供的1∶25 万地理信息数据，使用 ArcGIS 9.3软件进行处理，提取东北三省行政边界。

1.3研究方法

1.3.1反距离权重法。

确定性插值方法以研究区域内部的相似性或以平滑度为基础由已知样点来创建表面。在此以反距离权重法为例，对研究区进行空间插值。

反距离权重法插值与插值点与样点间的距离有关，插值点离样本点越远，所占权重越小；距样本越近，所占权重越大[7-9]。其基本公式如下：

Z（S0）=ni=1λiZ（Si） （1）

式中，Z（S0）为S0处的预测值；λi为各样点的权重；Z（Si）为Si处的采样值；n为要使用的插值点周围采样点的数量。使用该方法插值需要样本点的分布尽量均匀，且尽量覆盖整个区域。

反距离权重法是精确性插值，表面易受局部变化的影响，样点值过大或过小和样点值过于密集均会影响输出的表面，即当样本点存在各向异性时，邻域的形状、大小、方向均会对插值的结果产生影响。

1.3.2克里格法。除了确定性内插分析方法，还有基于统计模型的地统计内插方法，它不仅能生成预测表面，还能度量其预测的准确性和确定性。地统计是法国著名统计学家G.Matheron在大量理论研究的基础上逐渐形成的一门新的统计学分支。它以区域化变量为基础，借助变异函数，可以对数据进行的最优无偏内插估计。地统计与经典统计学的最大区别是地统计学既考虑到样本值的大小，又重视样本空间位置及样本间的距离，弥补了经典统计学忽略空间方位的缺陷[10]。笔者选用地统计分析中的普通克里格法及泛克里格法对研究区进行空间插值及预测。

克里格插值属于非精确性插值方法，它适用于当区域化变量存在空间相关性时，利用变异函数的结构特点及原始数据，对样点进行线性无偏、最优估计。反距离权重法仅考虑样本点与未知点间的距离，而克里格方法不只是考虑距离，同时利用变异函数和结构分析，进行样本点之间的空间分布方位关系分析。

普通克里格的估计公式为：

Z（x）=ni=1λiZ（xi） （2）

式中，Z（x）是在x位置上的估计值，Z（xi）是在xi位置的测量值，λi是分配给Z（xi）的残差的权重，n是用于估计过程的测量值的个数。

普通克里格是假设样本点变化呈正态分布且区域化变量期望值未知。如果数据在空间上存在明显的趋势，那么普通克里格方法就不再适用。此时，应该使用泛克里格方法进行分析。泛克里格方法假设数据中有主导趋势，而且该趋势可以用一个确定性的函数或多项式来拟合。泛克里格法即是找出这个趋势并对其分析得到拟合模型，对残差数据进行克里格分析，最后将二者结果加和得到最终结果。

1.3.3交叉验证。

交叉验证就是对于所有的站点，按顺序每次假设一个站点要素值未知，计算所有站点实测观测值与估计值的误差，可用计算后的统计数据来判断该模型是否适用于生成地图[11]。在ArcGIS中，统计数据有均值（Mean）、均方根预测误差（Root-Mean-Square）、平均标准误差（Average Standard Error）、标准平均值（Mean Standardized）、标准均方根预测误差（Root-Mean-Square Standardized）等。最优模型的特点是标准平均值最接近于零，均方根预测误差最小，平均标准误差最接近于均方根预测误差，标准均方根预测误差最接近于1[12]。通过比较上述统计数据和拟合效果对比图，来推出3种空间插值方法中的较优方法。

2结果与分析

2.1夏季平均气温趋势分析

空间趋势分析可以反映气温在该空间区域上变化的主体特征，反映气温空间分布的变化情况。准确地识别全局趋势，可以方便在ArcGIS地统计分析中全局趋势的剔除，从而能更准确模拟气温的短程随机变化[13]。

可以看出，1999、2004年东北三省平均气温投影到东西方向及南北方向上的趋势线从西到东、从南到北呈阶梯状平滑过渡，可得知东北三省气温趋势是从西到东、从南到北逐渐下降。

2.2夏季平均气温空间插值方法比较

2.2.1 插值预测。通过将1999和2004年的数据划分为training和test 2个数据子集，分别用普通克里格法、泛克里格法和反距离加权法3种空间插值方法进行插值生成预测图（图3）。

由图3可知，东北三省夏季平均气温表面上受纬度及海拔因素影响较大。

2.2.2精度检验。

从3种方法拟合效果（图4）可看出，泛克里格法的拟合线较接近理论拟合线，而普通克里格法和反距离权重法的拟合线偏角稍大。可见，从空间插值效果来看，采用泛克里格法较适合。

比较1999和2004年各自3种方法的training统计数据（表1）中的普通克里格和泛克里格的統计数据发现：标准平均值，普通克里格法和泛克里格法的均较接近于零；均方根预测误差，普通克里格法稍小于泛克里格法；平均标准误差，泛克里格法的值稍比普通克里格法更接近两者各自的均方根预测误差；标准均方根预测误差，2种方法的值均与标准值1相差较大。由此可见，普通克里格法与泛克里格法没有明显的差异，不能仅凭此判别哪一种更合适。

比较1999和2004年test统计数据（表2）中的普通克里格和泛克里格发现：标准平均值，普通克里格法和泛克里格法的均较接近于零，但后者更接近；均方根预测误差，普通克里格法稍大于泛克里格法；平均标准误差，泛克里格法的值与普通克里格法均很接近两者各自的均方根预测误差；标准均方根预测误差，2种方法的值均较接近标准值1，但泛克里格法的值小于普通克里格法。由此可见，泛克里格法比普通克里格法更合适。

3结论

利用交叉验证的方法对比了3种常用方法对东北三省夏季平均气温数据的预测效果，并借助ArcGIS地统计分析模块中预测图生成了3种方法下得到的1999与2004年的东北三省夏季平均气温分布图。

结果表明，3种空间差值法均能大致反映东北三省夏季平均气温分布特点，而从预测精度上看，泛克里格空间插值法精度优势更大，误差分布比较均匀，可以较好地体现东北三省夏季气温分布规律。

利用泛克里格法进行空间插值是较好的一种曲面插值方法，它考虑了数据中存在的变化趋势，兼顾了插值表面的平滑度和精度，在此次气温插值中得到了较好的体现，便于研究者直观发现气温空间分布特点，可为今后更有针对性地进行气温分布特点及演变特征提供参考。

克里格法为研究气温时空分布规律提供了方法，极大提高了空间内插的精度，在此结果上，可以进一步研究东北三省地区夏季多年平均气温时空变化规律，对东北三省的区域农业、生态环境、经济和人民生活有着重要意义。由于气象站点数量有限，气温数据存在缺值区域，使用空间内插方法是研究气温分布规律及演变特点的一个重要方法。东北三省夏季气温表面上受纬度及海拔因素影响较大，在进行空间插值时，需要考虑全局趋势的影响。

参考文献

[1]

廖顺宝，李泽辉，游松财.气温数据栅格化的方法及其比较[J].资源科学，2003，25（6）：83-88.

[2] 钞振华，杨永顺.基于地统计方法的中国西部气温空间插值研究[J].湖北大学学报（自然科学版），2011，33（2）：209-213，255.

[3] 张海静，周秉荣，金元锋，等.基于GIS技术的青海省最低气温空间插值方法探讨[J].草业科学，2010，27（9）：5-10.

[4] 毛明策.基于加密气象站观测资料的气温空间内插方法比较研究：以陕西省为例[J].西北农业学报，2010，19（4）：201-206.

[5] DODSON R，MARKS D. Daily air temperature interpolated at high spatial resolution over a large mountainous region[J].Climate resourse， 1997，8（1）：1-20.

[6] 董滿宇，吴正方.近50年来东北地区气温变化时空特征分析[J].资源科学，2008，30（7）：1093-1099.

[7] 杨忍，任志远.陕西省气温空间分布模拟研究[J].测绘科学，2010，35（4）：145-147.

[8] 廖顺宝，李泽辉.气温数据栅格化中的几个具体问题[J].气象科技， 2004，32（5）：352-356.

[9] 李新，程国栋，卢玲.空间内插方法比较[J].地球科学进展， 2000，15（3）：260-265.

[10] 汤国安，杨昕.ArcGIS地理信息系统空间分析实验教程[M].北京：科学出版社，2006：363-365.

[11] 党顺行，杨崇俊，王宇飞.卫星遥感海表温度反演研究[J].高技术通讯，2001，11（3）：49-52.

[12] 姚永慧，潘志强，孙英君，等.ArcGIS 地统计分析实用指南[M].北京：北京中科永生数据科技有限公司，2002：227-228.

[13] 于晓艳，马劲松，朱敬芳，等.基于地统计学的江西省年降水量插值研究[J].测绘科学，2011，36（4）：83-85，55.