体积拉伸流场中的纤维取向*

文劲松 范德军 谢海玲 尹晨欢 冯彦洪

(华南理工大学 聚合物新型成型装备国家工程研究中心∥聚合物成型加工工程教育部重点实验室， 广东 广州 510640)

废弃植物纤维/聚合物复合材料作为性能独特的新型材料，具有环境友好、可再生、性价比高等优点，因此得到了广泛的应用，但纤维的加入给复合材料的加工设备及加工工艺带来了巨大挑战.瞿金平等[1]创造性地发明了叶片挤出机，其基于拉伸流变的塑化输运机理与传统螺杆挤出机的剪切流变塑化输运机理具有本质区别.相对于以剪切流动为主的加工设备，叶片挤出机中熔体经历的热-机械历程短，所以对复合材料中纤维的破坏作用小，有利于纤维长径比的保持.针对纤维悬浮液中纤维的运动和取向行为，国内外均有较多研究.江青松、杨海等[2- 3]分别基于ARD-RSC纤维取向模型和Folgar-Tucker张量模型研究了纤维增强注塑成型流动过程中工艺参数与纤维取向分布之间的关系；沈苏华[4]采用将纤维取向分布函数分为平均和脉动两个部分的方法推导出了湍流流体中纤维的取向分布函数；黄达勇等[5]利用Moldflow研究了短玻纤增强PA66复合材料注塑成型过程中不同工艺参数和玻纤相互作用系数对纤维取向张量的影响.

基于拉伸流变的叶片挤出机与以剪切形变为主的螺杆类成型加工设备的塑化输运过程不同，相对于传统设备，其物料停留时间大大缩短，有效减少了加工过程对纤维的破坏，有利于纤维长径比的保持，从而能够得到综合性能更优的复合材料制品.目前鲜有体积拉伸形变动态加工过程中纤维复合体系混合分散过程的研究，因此，采用数值模拟的方法阐明纤维复合体系在体积拉伸流场下纤维的取向和分布规律，对设计聚合物加工设备和特定性能的复合材料具有重要的意义.文中运用粘弹性流动分析软件ANSYS POLYFLOW对叶片挤出机中一个叶片单元的流场分布进行数值模拟，使用数学软件Matlab计算取向分布函数，并对周向不同剖面上的纤维取向进行可视化显示，研究体积拉伸流场中的纤维取向分布规律，以期指导实际生产.

1 拉伸流场的数值模拟

1.1 几何模型

根据叶片挤出机的实际结构，一个叶片单元的几何模型如图1所示.

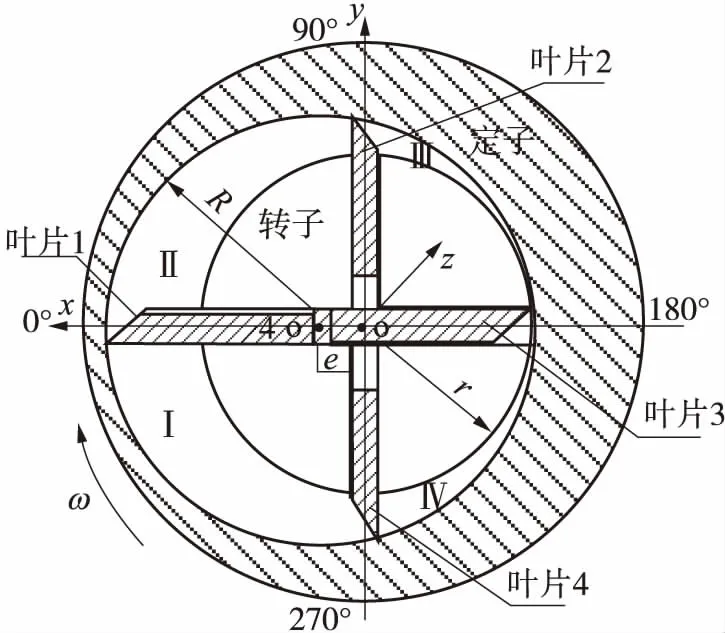
图1 叶片单元的结构示意图

图1中，定子半径R=24.5 mm，转子半径r=20 mm，转子与定子的偏心距e=4 mm，叶片径向长度L0=24.05 mm，叶片轴向长度L1=23.6 mm，叶片厚度h=4.5 mm，叶片顶端倒角为15°，叶片单元轴向长度L=24 mm，出入口轴向长度L2=5 mm.为便于说明，将4个叶片按照顺时针方向分别编号为1#、2#、3#、4#，同时将4个叶片形成的4个容腔按相同的顺序分别编号为容腔Ⅰ、容腔Ⅱ、容腔Ⅲ、容腔Ⅳ.

1.2 控制方程

文中研究内容属于含有运动件的瞬态流动分析，所以需要用到网格重叠技术(MST)、用户自定义函数(UDF)等技术，这两项技术在数值分析过程中涉及较多复杂因素，因此对叶片单元内的流体做出如下假设：①流体流动形式为等温层流；②流体为纯粘性非牛顿流体；③忽略壁面滑移；④流体不可压缩；⑤忽略重力和惯性.

根据以上假设，可以建立如下控制方程：

(1)

(2)

(3)

(4)

(5)

由于POLYFLOW在使用网格重叠技术时不能分析粘弹性流体，且聚合物在叶片挤出机中进行塑化输运时主要为粘性流动，所以文中选用广义牛顿流体的Bird-Carreau Law模型作为本构方程：

(6)

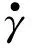
选用聚丙烯(PP，牌号N-Z30S，粒料，中石化集团广州分公司生产)作为研究材料.通过Anton Paar MCR302旋转流变仪测得该材料的流变数据，设置测试条件如下：温度，190 ℃；剪切速率范围，0.001～100 s-1；测试样品是由平板硫化机制得的厚度为1 mm、直径为25 mm的圆形薄片.将测得的黏度与剪切速率数据导入POLYFLOW的POLYMAT模块，选择Bird-Carreau Law模型进行拟合，得到实验所用材料的拟合曲线，如图2所示.

图2 POLYMAT拟合曲线

从POLYMAT中可以得到Bird-Carreau Law模型对应的各个参数值：η0=1 162 Pa·s，η∞=0.23×10-3Pa·s，λ=0.67，n=0.64.

1.3 网格划分和边界条件

模型的网格质量和数量直接影响数值计算的精度和速度.文中使用CFD软件POLYFLOW的前处理模块GAMBIT进行建模和网格划分.1个叶片单元包括1个流体区和4个固体区(即4个叶片)，其中因为流体区为主要计算区域，所以流体区的网格要精细划分，固体区网格的存在是为了适应网格重叠技术，将运动部件上的边界条件转换到流体区域.叶片和流体区域的网格划分如图3所示.

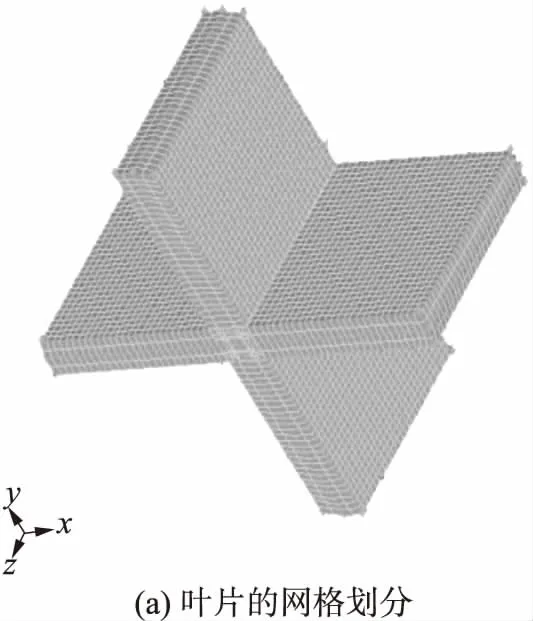
图3 叶片单元网格的划分

此外，需要对单元出入口、定子内壁及转子外壁设置边界条件，4个叶片的运动较为复杂，因此需要用户自定义函数来加以定义.

1.4 叶片单元内的流场分布

分散指数可以衡量流场的分散混合能力，分散指数的定义如下[6]：

(7)

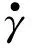
(8)

E为应变速率张量.

λm=0时流体表现为纯柱塞流动，λm=0.5时流体表现为纯剪切流动，λm=1时流体表现为纯拉伸流动，故分散指数越接近1说明拉伸流动所占比例越大.为研究叶片单元中流场的性质，文中选择1s后、转速为60r/min时的叶片单元入口、出口及z=15mm位置处的分散指数分布云图，如图4所示.

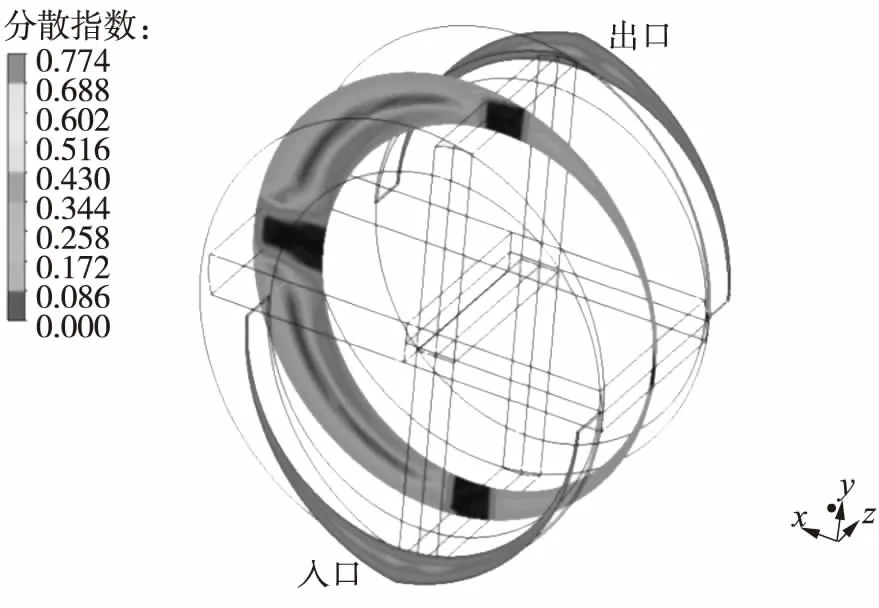
图4 转速60 r/min时的分散指数分布

图4中叶片覆盖区域分散指数为0；出口和入口分散指数均较小，说明出口和入口处的流场以剪切流场为主；在出口和入口的中心位置，分散指数大于0.5，表明此处的流场中含有拉伸流场成分.分散指数的分布是因为入口和出口内壁对熔体有拖拽作用，熔体受到剪切力的作用，而在中心位置，由于熔体随着转子转动从入口处流入下一个容腔内，使得入口处的熔体变少，容腔内压力降低，产生压力降，从而对熔体产生一定的吸纳作用，表现为拉伸流动.此外发现在沿z轴12 mm的截面处分散指数均较大，除了转子和定子壁面处外，其他位置的分散指数均大于0.5，最大可达0.774，说明在叶片单元的主要挤压区域存在较强的拉伸流动.

2 纤维取向的数值计算

2.1 单根纤维取向状态的描述

使用沿取向方向的单位矢量P来描述单根纤维的取向[6- 7].如图5所示.

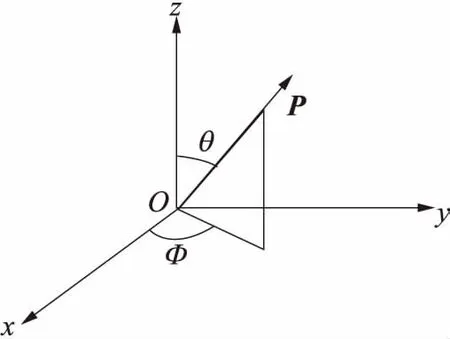
图5 单根纤维的取向

在球坐标系中只需要用两个变量(θ，Φ)就可以对P进行描述，在直角坐标系中P可以表示为[8]

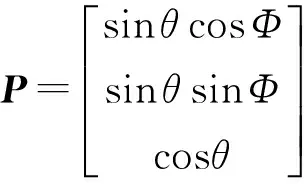
(9)

在实际应用中，流体中存在大量的纤维，若要计算出每一根纤维的取向状态将花费大量的时间，因此可以采用统计平均的方法来研究纤维取向状态.引入一个体积单元，并认为这一体积单元在宏观上大到足够容纳很多纤维，在微观上又足够小，以至于包含在其中的纤维都有均一的取向状态.在这一体积单元内的纤维取向状态可以用两种方法来描述：第1种方法基于纤维取向分布函数ψ(θ，Φ)，这一函数描述了纤维粒子在某个方向上取向的概率；第2种方法基于空间统一的平均取向状态.文中选择第1种方法描述纤维的取向状态.

2.2 拉伸流场作用下纤维的取向分布函数

取向分布函数基于以下假设[9]：①纤维为刚性圆柱体，具有均一的长度和直径；②纤维足够大，可以忽略布朗运动；③悬浮液不可压缩；④粘性力足够大，重力和浮力可以忽略；⑤初始纤维随机均匀分布；⑥无外部作用力.

取向分布函数是描述纤维取向状态最常用也是最易理解的形式，纤维取向分布函数ψ(θ，Φ)或ψ(p)代表在一个小的研究体积域内纤维沿着给定的取向方向取向的概率.在整个区域中由于每一个纤维粒子必然沿某个方向取向，则分布函数在整个区域中的积分值为1[10]，即

(10)

这就是纤维分布函数的归一化性质.由于纤维并没有头和尾的区分，可以得到相应的对称性质[11]，即

ψP=ψ(-P)

(11)

文献[12- 15]的研究表明，对于初始自由取向的纤维，其分布函数的三维方程可以简化为

(12)

式中：t为时刻；Δij为位移梯度张量，其表达式为

Δij=(∂Xi/∂xj)

(13)

Xi是0时刻的位置矢量，xj是当前时刻的位置矢量.

位移梯度张量Δij必须满足如下条件：

(14)

式中，Wkj为涡量张量，Ekj为应变速率张量.在初始时刻，Δij=δij[16]，即

(15)

δij表示纤维取向的概率.

计算纤维的取向分布函数需要纤维所在流场的速度梯度张量.在叶片挤出机等复杂流场中，混合物熔体沿着流线流动，因此可通过POLYFLOW软件的后处理模块CFD-Post对POLYFLOW求解的结果进行分析，导出沿流线方向各节点处的速度梯度张量.

文中假设初始时刻纤维随机取向，即可取初始时刻的位移梯度张量Δij=δij，纤维在每个节点处停留的时间可以通过两相邻节点的距离除以速度近似得到.将流线上第1个节点处的速度梯度张量和时间代入，使用Matlab的语句“[T，Y]=ode45(odefun，tspan，y0)”求解位移梯度张量的微分方程组，即可得到该节点的位移梯度张量，然后将第1个节点的位移梯度张量作为第2个节点的初始值，得到第2个节点处的位移梯度张量，如此即可计算出流线上每个节点处的位移梯度张量，再将位移梯度张量代入式(12)，计算各个节点处的取向分布函数.使用Matlab编程将取向分布函数可视化，即可得到各个节点处取向分布函数的最大值，此时所对应的方向即为该节点处纤维的取向方向.

以入口处和容腔I的内外表面为例来说明数值模拟纤维取向情况的方法.由于定子内壁和转子外壁接触的表面没有速度，所以在偏移内外表面1 mm处选取剖面，内外表面的选取如图6所示.

所取入口处及容腔Ⅰ内外表面上的速度分布如图7所示.

图6 入口处及容腔I内、外表面的选取

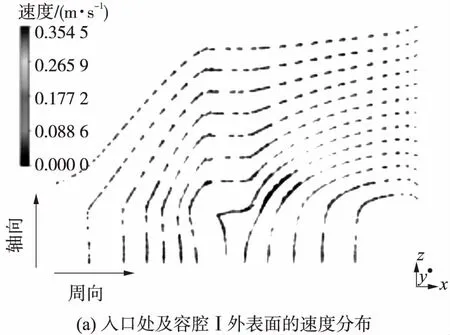
图7 入口处及容腔I内、外表面的速度分布

从图7可以看出，在入口处熔体沿着轴向(即挤出方向)流动，而在远离入口处熔体沿着与轴向和周向呈一定夹角的方向流动，且与周向的夹角较小.根据每个节点处纤维取向分布函数的最大值对应的θ和Φ求得纤维优先取向的方向，将纤维取向可视化，得到纤维的取向分布情况.

由图8可以看出，在入口处纤维均是沿轴向(即挤出方向)取向，这是因为在入口处熔体的压力降较大，促使纤维沿着压力降的方向流动，从而使纤维沿着挤出方向取向.而在远离入口的内外表面，纤维既不是沿周向方向取向，也不是沿轴向方向取向，而是沿与周向和轴向方向皆呈一定夹角的方向取向，且在外表面上纤维取向方向与周向方向的夹角较在内表面上纤维取向方向与周向方向的夹角小.这是因为熔体在叶片单元中流动时既受转子旋转作用的影响又受挤出方向排料作用及吸纳作用的影响，另外从图4可以看出，在外表面处分散指数较大，拉伸流场占优，而在内表面处分散指数较小，剪切流场占优，这也再次说明拉伸流场更有利于纤维的取向.与图7进行对比发现，纤维的取向分布与内、外表面上的速度分布一致.这也在一定程度上反映了纤维取向分布数值模拟的准确性.

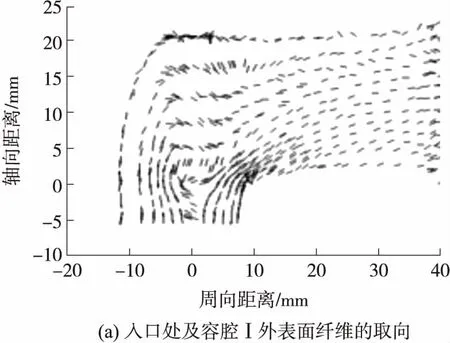
图8 入口处及容腔Ⅰ内、外表面纤维的取向

使用与图6所示同样的方法沿周向选取与转子轴心的距离s分别为21.5、22.5、23.5、24.5、25.5、26.5 mm的6个剖面，导出各个节点处的速度梯度张量，计算各个剖面上的纤维分布函数.图9为转速为60 r/min时6个不同剖面上纤维取向的可视化图.

图9中入口点在正方向的属于从容腔I进入的纤维，入口点在负方向的属于从容腔Ⅳ进入的纤维.从图9中可以发现：

(1)从容腔I进入的纤维在各个剖面上的取向较为一致，在入口处纤维主要沿轴向即挤出方向取向，而在远离入口处，由于纤维既受到吸纳作用的影响又受到转子旋转运动的影响，纤维主要沿与周向和轴向呈一定夹角的方向取向；

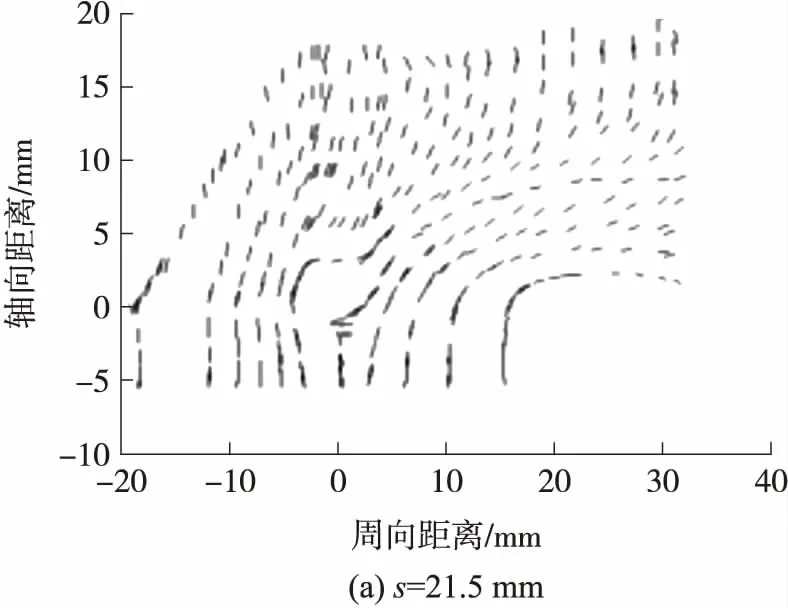
图9 不同剖面上纤维取向分布函数的可视化

(2)从容腔Ⅳ进入的纤维在入口处各个剖面上的取向方向较一致，均沿轴向(即挤出方向)取向，而在远离入口处，纤维的取向方向在各个剖面上有较大的差别；

(3)在靠近转子的剖面(即s=21.5～22.5 mm)上，从容腔Ⅳ进入的纤维在远离入口处的取向方向相对于入口处的取向方向有较明显的改变，沿与周向和轴向呈一定夹角的方向有一定规律的取向，但取向方向与周向的夹角相对较大；在远离转子的剖面(即s=23.5～26.5 mm)上，纤维取向方向相对于入口处的取向方向发生了明显的变化，各个剖面上纤维取向方向与周向的夹角有所不同，从剖面s=23.5 mm到剖面s=26.5 mm，纤维取向方向与周向的夹角由大逐渐变小，又由小逐渐变大.

从容腔I进入的纤维取向方向与从容腔Ⅳ进入的纤维取向方向有较大差别，主要原因为从容腔Ⅳ进入的纤维随着转子旋转进入容腔I的位置后，其运动的主要动力来自叶片的推动作用，而从容腔I进入的纤维不仅受到叶片推动作用的影响还受到其他熔体推动作用的影响，故从不同容腔进入的纤维取向方向不一致.此外，在图4中靠近转子处，分散指数小于0.5，处于0.3～0.4之间，说明此处的流场以剪切流场为主；而在稍微远离转子处，分散指数减小，处于0.2～0.3之间，说明此处剪切流场减弱，柱塞流所占比例增加；在叶片单元的中心位置，分散指数较大，处于0.5～0.8之间，说明此处的流场以拉伸流场为主；而在叶片单元的外表面处，分散指数虽然也大于0.5，但是明显比中心位置小，说明此处拉伸流场所占比例减弱.

对比纤维的取向分布图和叶片单元分散指数分布云图发现，剪切流场和拉伸流场均有利于纤维的取向，柱塞流占优的流场中纤维的取向方向基本不变;在以拉伸流场为主的流场中，纤维的取向方向与周向的夹角相对于以剪切流场为主的流场中纤维的取向方向与周向的夹角更小，说明拉伸流场相对于剪切流场更有利于纤维的取向.

3 数值计算结果的实验验证

采用数值模拟方法研究了叶片挤出机叶片单元中不同剖面上纤维的取向情况[17]，通过数学建模和理论推导的方法研究了拉伸流场作用下植物纤维的取向行为，并通过骤冷拆机实验对研究结果进行了验证，利用SEM观察了PP/SF(聚丙烯/剑麻纤维)复合材料沿挤出方向和垂直挤出方向两个面上纤维的取向行为，如图10所示.

从图10(a)可以看出，纤维沿挤出方向发生明显的取向，纤维的取向方向并没有完全和挤出方向平行，而是呈一定夹角，这主要是因为叶片挤出机中存在拉伸流场，有利于纤维的取向，另外，转子的旋转会带动熔融的复合材料旋转，也会造成纤维的取向方向与挤出方向产生一定夹角.从图10(b)中也可以观察到脆断时纤维从基体中被拔出而留下的孔洞，说明纤维沿挤出方向发生了取向.而且从图10(b)中还可以看出，纤维在基体中分布较均匀，没有发生明显的团聚现象，说明在叶片挤出机中纤维的分散和取向效果较好.以上现象与数值模拟所得结论一致.

图10 PP/SF复合材料脆断的SEM图

4 结论

文中采用粘弹性流动分析软件POLYFLOW和数学软件Matlab分析拉伸流场作用下的纤维取向，得到以下结论：

(1)在叶片挤出机流场分布中，出入口边缘处分散指数相对较小，说明以剪切流场为主，而出入口中心和叶片单元内部分散指数均大于0.5，说明以拉伸流场为主；

(2)从纤维取向分布函数演化方程的求解结果可以看出，在叶片单元入口处纤维主要沿轴向即挤出方向取向，在远离叶片单元入口处纤维主要沿与周向和轴向呈一定夹角的方向取向，结论与叶片挤出机体积拉伸实验结果一致；

(3)对比纤维的取向分布图和叶片单元中分散指数的分布云图发现，剪切流场和拉伸流场均有利于纤维的取向，柱塞流占优的流场中纤维的取向方向基本不变，且在以拉伸流场为主的流场中纤维的取向方向与周向的夹角要比在以剪切流场为主的流场中纤维的取向方向与周向的夹角更小，说明拉伸流场相对于剪切流场更有利于纤维的取向.

：

[1] 瞿金平，冯彦洪，何和智.塑料和植物纤维复合材料的叶片式加工设备及加工设备:102126262A [P].2011- 07- 20．

[2] 江青松，柳和生，熊爱华，等.长纤维增强聚合物注塑流动纤维取向分布数值模拟 [J].高分子材料科学与工程，2015，31(3)：123- 127．

JIANG Qing-song，LIU He-sheng，XIONG Ai-hua，et al.Numerical simulation on the fiber orientation distribution during flow in injection molding of long fiber reinforced polymer [J].Polymer Materials Science and Engineering，2015，31(3)：123- 127．

[3] 杨海，李再轲，陈增红，等.注塑工艺参数对矩形薄壁件纤维取向影响模拟研究 [J].广东化工，2016，43(17):47- 48．

YANG Hai，LI Zai-ke，CHEN Zeng-hong，et al.Study on effect of injection molding parameters on fiber orientation based on rectangular thin walled part [J].Guangdong Chemical Industry，2016，43(17):47- 48．

[4] 沈苏华.纤维悬浮湍流中纤维取向和流变特性研究[D].杭州:浙江大学，2010．

[5] 黄达勇，丁智平，荣继刚，等.短玻纤增强工程塑料纤维取向张量影响因素研究 [J].湖南工业大学学报，2016，30(3):12- 18．

HUANG Da-yong，DING Zhi-ping，RONG Ji-gang，et al.Research on influential factors of fiber orientation tensor of short-glass fiber reinforced engineering plastics [J].Journal of Hunan University of Technology，2016，30(3):12- 18．

[6] 何红，陈雄兵.长方体状注射模腔内纤维取向分布模拟计算 [J].塑料，2013，42(4):1- 5．

HE Hong，CHEN Xiong-bing.Numerical simulation of fiber orientation distribution in cuboid shaped plastic injection mold cavity [J].Plastics，2013，42(4):1- 5．

[7] 秦计生，彭雄奇，申杰，等.考虑纤维方向分布的玻纤增强PP复合材料拉伸性能 [J].复合材料学报，2013，30(4):53- 58．

QIN Ji-sheng，PENG Xiong-qi，SHEN Jie，et al.Tensile properties of glass fiber reinforced PP composite considering fiber orientations [J].Acta-Materiae Compositae Sinica，2013，30(4):53- 58．

[8] 赵建，曲敏杰，夏英，等.纤维含量对注塑制品残余应力影响的数值模拟 [J].高分子材料科学与工程，2014，30(4):127- 131．

ZHAO Jian，QU Min-jie，XIA Ying，et al.Numerical simulation of the effect of fiber content on residual stresses in fiber reinforced injection molding [J].Polymeric Mate-rials Science and Engineering，2014，30(4):127- 131．

[9] WEN J.S.，LEI S.K，LIANG Y H，et al.Numerical simulation of mixing characteristics in a vane extruder [J].J Macromol Sci(Part B)，Phys，2014，53:358- 369．

[10] GIVLER R C，CROCHET M J，PIPES R B.Numerical prediction of fiber orientation in dilute suspensions [J].Journal of Composite Materials，1983，17(4):330- 343．

[11] LIPSCOMB II G G，DENN M M，HUR D U，et al.The flow of fiber suspensions in complex geometries [J].Journal of Non- Newtonian Fluid Mechanics，1988，26(3):297- 325．

[12] 熊爱华，柳和生，黄益宾，等.长玻纤增强聚合物注塑充填行为和纤维取向模拟 [J].高分子材料科学与工程，2015，31(10):110- 114．

XIONG Ai-hua，LIU He-sheng，HUANG Yi-bin，et al.3D simulation of filling behavior and fiber orientation for Long glass fiber reinforced polymer composites during injection molding process [J].Polymeric Materials Science and Engineering，2015，31(10):110- 114．

[13] DINH S M，ARMSTRONG R C.A rheological equation state for semi-concentrated fiber suspensions [J].Journal of Rheology，1984，8(3):207- 279．

[14] YAMANOI M，MAIA J M.Analysis of rheological pro-perties of fiber suspensions in a Newtonian fluid by direct fiber simulation(Part 3):behavior in uniaxial extensional flows [J].Journal of Non-Newtonian Fluid Mechanics，2010，165(23):1682- 1687．

[15] RAMAZANI A，AIT-KADI A，GRMELA M.Rheological modeling of short fiber thermoplastic composites[J].Journal of Non-Newtonian Fluid Mechanics，1997，73(3):241- 260．

[16] CAO Shan，XIE Shang-ran，LIU Fei，et al.Numerical and experimental analysis of polarization dependent gain vector in Brillouin amplification system [J].Optics Communications，2017，89:23- 28．

[17] 黄赞.拉伸力场支配作用下植物纤维复合材料混合过程模拟研究 [D].广州:华南理工大学，2014．