GFRP-混凝土组合连续板的静力性能试验研究*
佟兆杰 黄侨† 鲍卫刚 万世成
(1.东南大学 交通学院, 江苏 南京 211189; 2.中交路桥技术有限公司, 北京100011)
桥面板作为直接承受车辆荷载的桥梁构件,在环境侵蚀、超载等因素的共同作用下,成为钢-混组合梁桥中最容易出现病害的构件之一[1].而FRP(纤维增强复合材料)-混凝土组合桥面板具有耐腐蚀、施工便利的特点,可成为提高组合梁桥桥面板耐久性、延长桥面板使用寿命的技术选项之一.由于FRP材料低弹模高强度的特性,在满足正常使用要求的条件下,该类组合板的极限承载力很高,其在正常使用荷载下的变形及裂缝宽度则成了重要的设计控制指标.目前对该类组合板的研究主要集中于截面形式以及极限状态下的受力性能[2- 8],对于正常使用状态下的受力性能的研究还不多.完善FRP-混凝土组合板在正常使用状态下的力学性能研究,将有利于该种结构在桥梁工程中的应用.
目前国内外对于FRP-混凝土组合板在正常使用状态下的研究主要集中于简支板的变形计算,对于连续板的研究不多,对其负弯矩区裂缝宽度的研究就更加少见.Hall等[9]基于钢筋混凝土的分析方法,采用跨中截面的开裂刚度计算了简支单向组合板的变形,但未考虑非开裂截面刚度的影响;Alagusundaramoorthy等[7]对FRP-混凝土组合板的受力性能进行了研究,并通过多点变形反推了FRP-混凝土组合连续板正负弯矩区的刚度,但未能给出组合连续板的变形计算方法;Nelson等[10]采用板的变形理论给出了考虑FRP正交异性的FRP-混凝土组合双向板的变形计算方法;黄辉等[11]采用共轭梁法对钢梁支撑条件下的FRP-混凝土空心连续单向板的内力分布进行了计算与分析,验证了该方法在组合板内力重分布计算中的可行性.
目前,还缺少FRP-混凝土连续单向板在正常使用荷载下的变形计算方法以及相应的试验验证.此外,FRP-混凝土连续板负弯矩区主要由钢筋以及FRP板共同承受拉力,对这种情况下负弯矩区裂缝宽度的计算方法也缺少研究.为了提高桥面板的耐久性,研究GFRP(玻璃纤维增强复合材料)-混凝土连续板的变形和裂缝宽度计算方法,文中根据黄侨等[12]提出的GFRP-混凝土组合板结构形式,进行了3片负弯矩区采用不同配筋率的GFRP-混凝土连续板的静力试验,重点关注了变形、裂缝开展及破坏模式,并探讨了GFRP-混凝土连续板在正常使用状态下的变形及负弯矩区裂缝宽度的计算方法.
1 试验概况
1.1 试件设计及材料参数
试验中设计了3块单向受力的两跨连续GFRP-混凝土组合桥面板,GFRP底板与混凝土的交界面上均采用湿粘结的连接方式.此处的湿粘结是指在GFRP板表面涂环氧树脂并在胶水凝固前浇筑混凝土,通过环氧树脂将GFRP板与混凝土底面粘接起来的技术.试验中仅在GFRP底板表面涂抹环氧树脂.GFRP-混凝土连续板的计算跨径为2×1.6 m,在混凝土顶层分别通长布设5φ10 mm、5φ12 mm和5φ14 mm的HPB300光圆钢筋,其配筋率分别为0.54%、0.78%、1.1%.在中支点紧邻GFRP底板处的混凝土中布设φ6 mm的HRB400带肋钢筋以观测混凝土纵向应变,见图1(a).GFRP板为带翼缘的槽型板材,板高80 mm,板宽3×200 mm.GFRP板的截面尺寸和几何形状如图1(b)所示,试验梁的纵断面见图1(c),相关的设计参数及实测的各试件的材料性能指标见表1.
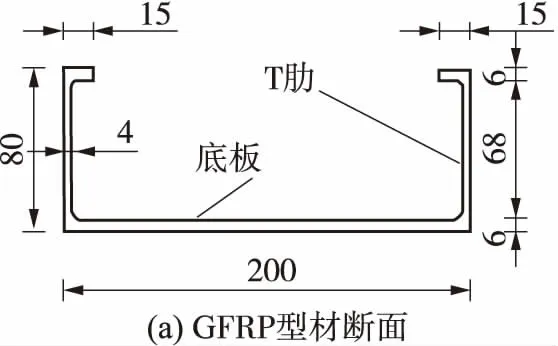
图1 试件详图(单位:mm)
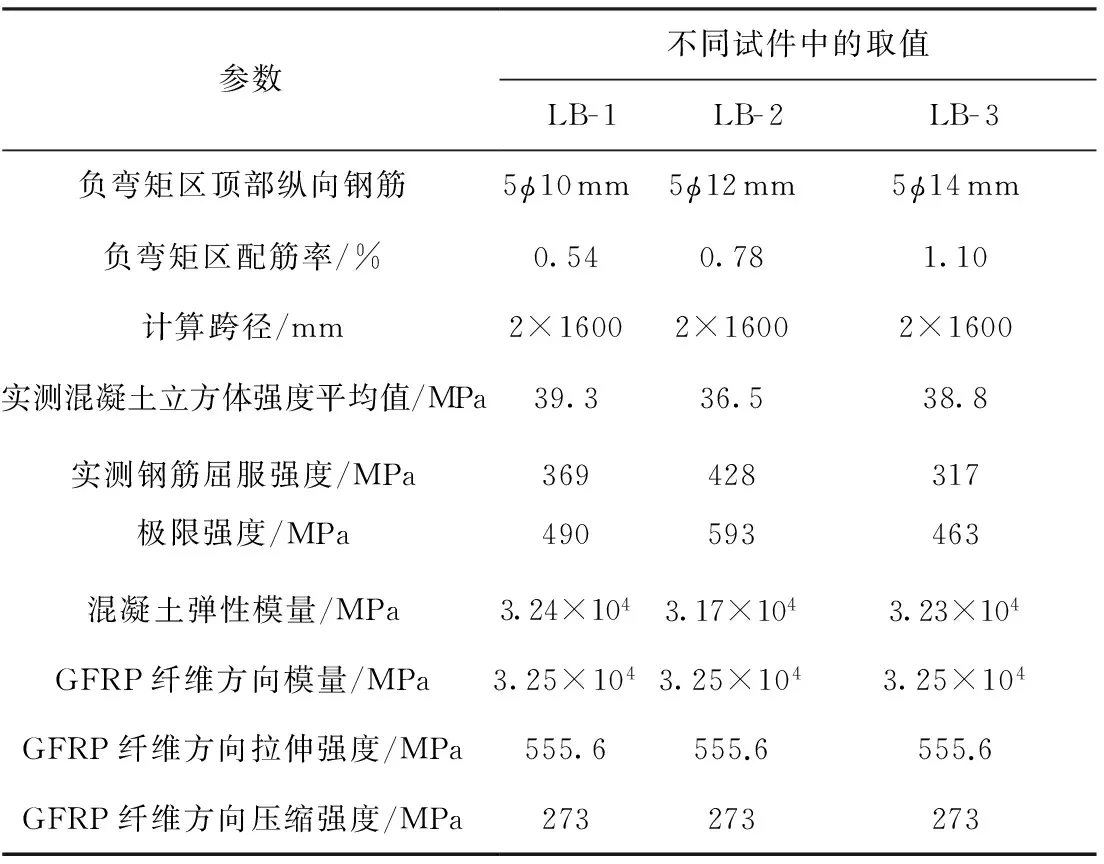
表1 实测试件的材料参数
1.2 加载装置及测点布设
试验中通过油泵控制两个50 t千斤顶同步加载,加载点位于各跨的跨中.在支座及千斤顶上布设压力传感器获取连续板的内力分布.在跨中、板端和中支点处布设电子位移计、百分表测量连续板的变形,板端布设千分表测量GFRP板与混凝土间的界面滑移.在跨中和中支点的GFRP板、钢筋以及混凝土表面分别布设应变片,以测量跨中和中支点断面的应变,进而换算得到应力.其中,参考文献[13]的方法,在负弯矩区钢筋上采用规格为20×3 mm的应变片,以此获得钢筋的平均应变.试验中采用东华3816 N型静态应变仪测取应变和位移数据,试验加载方式及测点布置见图2.
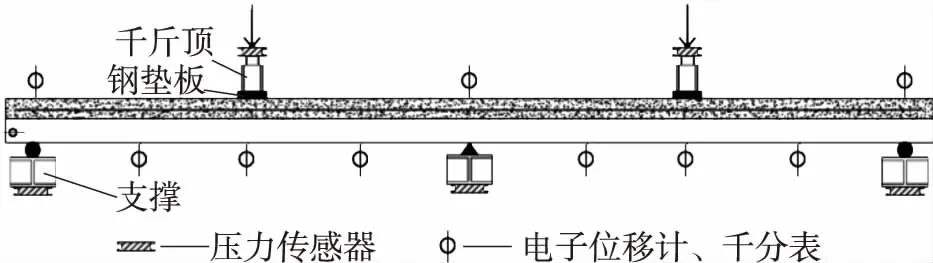
图2 加载装置及测点布置图
2 试验结果及分析
2.1 破坏模式及裂缝分布形态
对于LB-1试件,加载至40 kN时在负弯矩区混凝土顶面观测到第1条横向裂缝,裂缝宽度为0.12 mm;加载至140 kN时裂缝宽度达到1.96 mm,此时停止裂缝观测.加载至255 kN时,梁两侧面在千斤顶加载点附近出现从GFRP肋板与混凝土交界处延展上来的斜向裂缝.加载至260 kN时,斜裂缝延展到混凝土顶面,GFRP与混凝土开始上下分离,连续板试件破坏.继续加载,荷载值降低,变形明显增大,GFRP板与混凝土分离明显,此时荷载完全由GFRP板承担.停止油泵供油后,GFRP板与混凝土的分离变形部分恢复,最终荷载稳定在160 kN.将油泵卸载到零,连续板的变形仍有一定的弹性恢复,说明未发生弯剪破坏段的GFRP板与混凝土之间仍有牢固的粘结.对破坏后的试件进行裂缝观测,可以看到破坏斜裂缝从中支点延伸到加载点,见图3(a)和3(b).
对于LB-2试件,加载至40 kN时在负弯矩区混凝土顶面出现第1条横向裂缝,由于负弯矩区配筋率提高,混凝土顶面的横向裂缝宽度为0.06 mm;加载至190 kN时裂缝宽度也仅为1.28 mm,此时停止裂缝观测.加载至185 kN时在侧面出现斜裂缝,280 kN时斜裂缝延伸到板顶部,试件破坏,停止加载,其破坏模式见图3(c).

图3 GFRP-混凝土连续板破坏形态
对于LB-3试件,首条裂缝出现在35 kN时,40 kN时横向裂缝宽为0.1 mm,225 kN时裂缝宽度为1.16 mm,此时停止对裂缝宽度的观测;加载至200 kN时出现斜向裂缝,随着荷载增大,裂缝向加载点处延伸,并且出现GFRP板与混凝土剥离的现象.最后,加载至300 kN时斜裂缝延伸到加载点混凝土顶面,试件破坏模式见图3(d).
试验结果表明,在极限状态下3块GFRP-混凝土连续板的破坏模式与文献[7]中组合板的破坏模式相似,均为弯剪段的混凝土剪坏,见图3.分析其原因主要是:在满足变形要求的条件下,GFRP-混凝土组合板试件的底板较厚,其抗弯承载力较高,从而使组合板发生了混凝土的剪切破坏.3块板的主要试验结果见表2,表中的理论计算方法详见第3.1节.荷载-中支点顶面裂缝宽度关系及裂缝分布形态见图4-6.
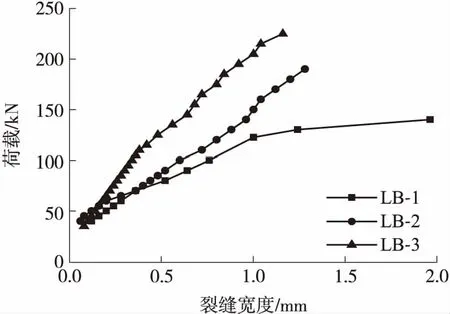
图4 实测的3试件荷载-裂缝宽度关系
从图4中可以看出,裂缝宽度随着荷载的增大而增大,并且增大速率逐渐增加.这是由于随着荷载的增大,负弯矩区钢筋逐渐屈服,其对裂缝的限制作用逐渐减弱.
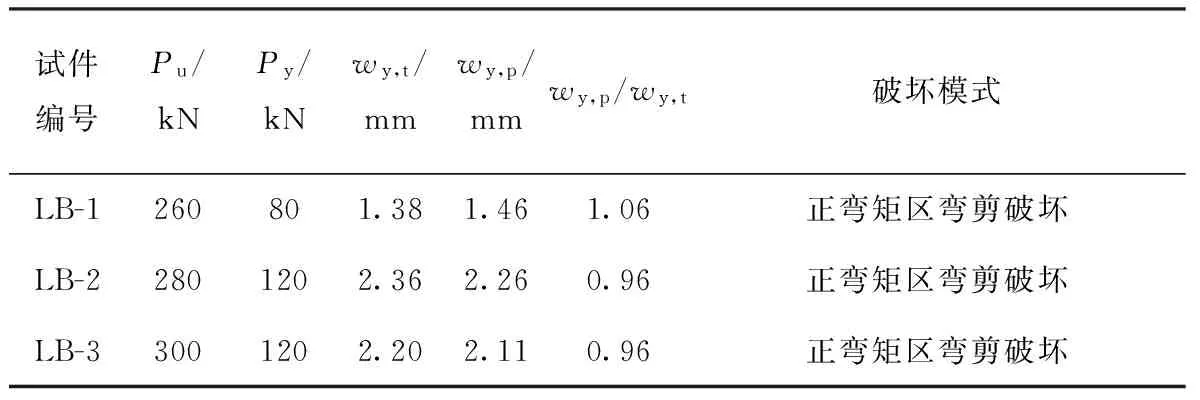
表2 试验与分析结果1)
2.2 荷载-变形及板端滑移
图7给出了3个试件的荷载-变形曲线.从图中可知,连续板的变形可以划分为3个阶段:阶段1,混凝土开裂前,荷载-变形曲线呈直线状;阶段2,混凝土开裂后,连续板刚度降低,变形增加;阶段3,钢筋屈服后,伴随着内力重分布、混凝土非线性效应的增加以及跨中正弯矩区GFRP板与混凝土间出现微小的滑移,荷载-变形曲线的非线性虽有增加但仍接近于直线变化.通过比较不同配筋率的连续板荷载-变形曲线可以看出,负弯矩区受拉钢筋屈服前变形曲线基本一致,钢筋屈服后配筋率高的连续板的变形较小.这是由于混凝土开裂后,配筋率低的连续板负弯矩区受拉钢筋先进入屈服状态,导致变形增大.
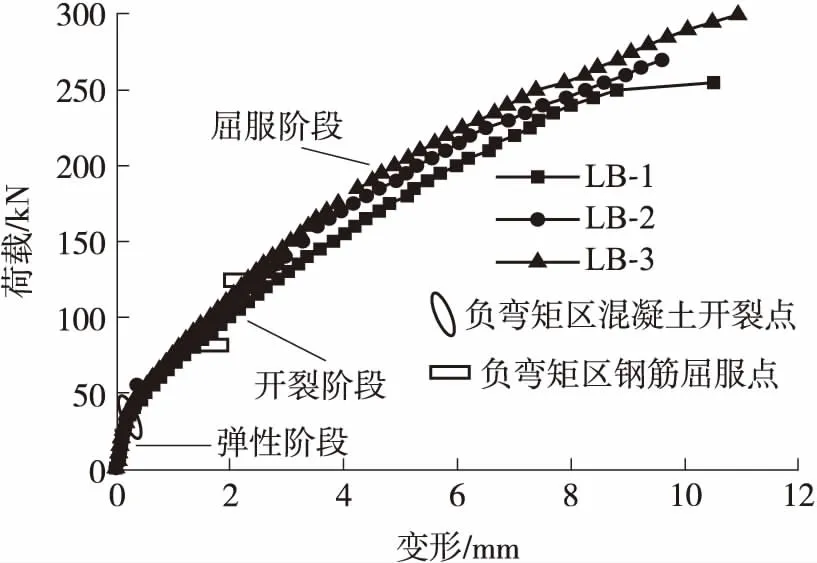
图7 荷载-变形曲线
破坏时,3块连续板试件的板端滑移量均小于0.002 mm,因此可以忽略板端的界面滑移.
2.3 应变分布
图8为实测的GFRP-混凝土组合连续板正负弯矩区的应变分布.从图中不难看出:当荷载小于0.63Pu时,正弯矩截面基本符合平截面假设;当荷载大于0.63Pu时,在GFRP肋板顶面与混凝土的交界面出现斜裂缝,造成了GFRP肋板与混凝土界面的相对滑移,且随着荷载的增大滑移明显增大;当达到极限荷载时,LB-1、LB-2、LB-3混凝土顶面压应变分别为2 868×10-6、2 669×10-6、2 346×10-6,其值均未达到3 000×10-6.这是由于在满足变形要求的条件下,GFRP-混凝土组合桥面板正弯矩截面的GFRP底板较厚,造成了正弯矩截面的抗弯承载力高于组合板的抗剪承载力,因而未发生弯曲破坏.对于中支点负弯矩截面,大约在0.43Pu作用时受拉钢筋屈服.通过上、下两层钢筋应变以及GFRP板应变的连线可以看出,在整个加载过程中,平截面假定基本成立.
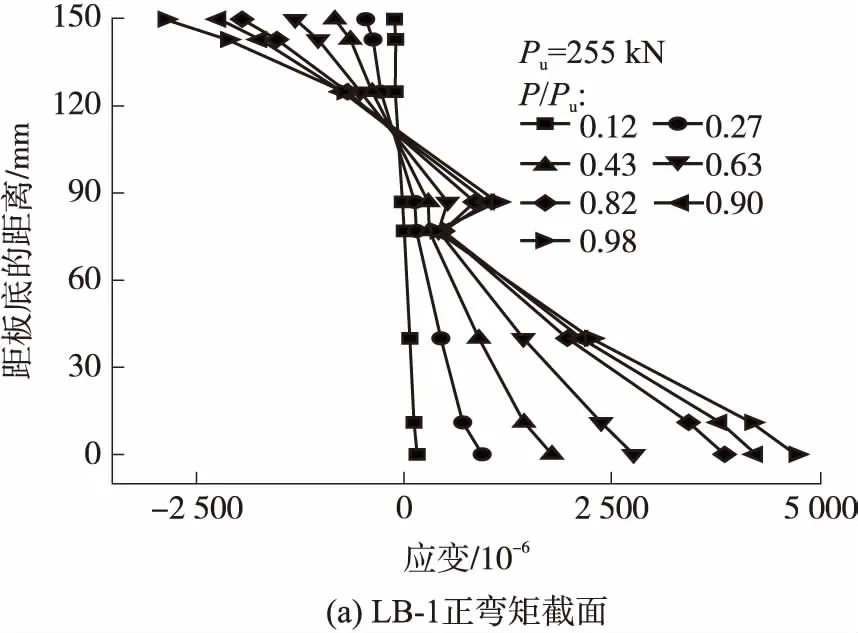
图8 连续板控制截面的实测应变分布图
2.4 荷载-支反力关系
图9为负弯矩区受拉钢筋屈服前的GFRP-混凝土连续板的荷载-支反力关系图.试验中Rs-t为实测的边支点反力,Rm-t为实测的中支点反力,Rs-p为考虑了混凝土非开裂截面刚度影响并按等效刚度计算的边支点反力,Rm-p为中支点反力计算值.从图9中可以看出,在正、负弯矩区采用等效刚度获得的组合板支反力计算结果与实测结果吻合良好,即可以采用等效刚度来获取GFRP-混凝土组合连续板的内力分布.连续板内力分布的计算方法见第3.1节.
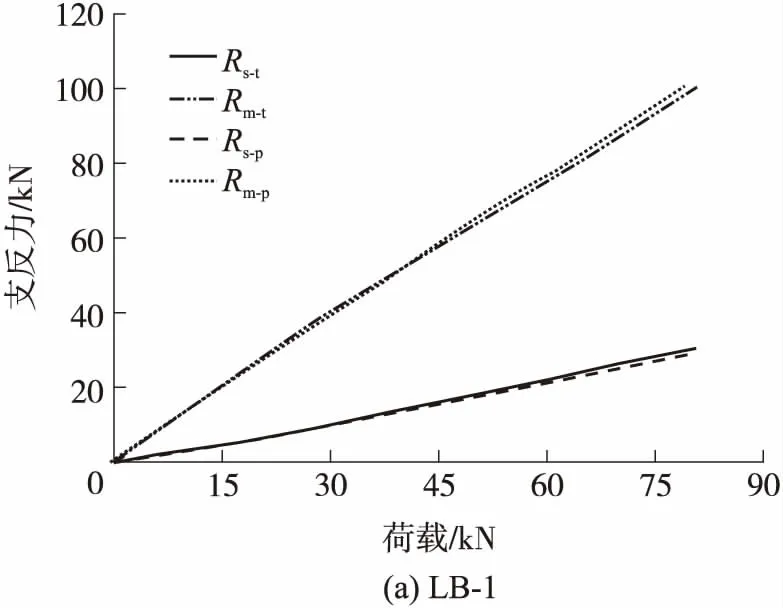
图9 荷载-支反力关系图
3 连续板的变形及裂缝计算
3.1 变形计算
基于实测的截面应变分布可以发现,在钢筋屈服前组合板的正、负弯矩区均可保持平截面假定.因此,在负弯矩区钢筋屈服前,组合板正负弯矩区的刚度可以通过换算截面法获得.图10给出了组合板正、负弯矩区开裂截面的换算刚度计算图示,其中αEG=EG/Ec,αEs=Es/Ec,EG、Es和Ec分别为GFRP、钢筋和混凝土的弹性模量.
获取了组合板正负弯矩区的开裂刚度之后,还需对开裂刚度进行修正以考虑裂缝间非开裂截面的影响.Hall等[9]采用了跨中截面的开裂刚度计算FRP-混凝土简支板的变形,但实际上FRP-混凝土组合板在开裂区与钢筋混凝土类似,也存在开裂截面和非开裂截面(如图11所示).如果只使用开裂截面刚度进行变形计算,将使计算值偏大,因而需使用考虑非开裂截面的等效刚度进行变形计算.在受力全过程中GFRP板与混凝土牢固地粘接在一起,可视其为混凝土板中的底层钢筋,因此可以参照钢筋混凝土中考虑等效刚度的算法进行等效刚度的计算.在此采用JTG D62—2004《公路钢筋混凝土及预应力混凝土桥涵设计规范》[14]中的等效刚度方法来计算GFRP-混凝土连续板正负弯矩区的等效刚度,其计算公式如式(1)所示.将通过换算截面法获取的正、负弯矩区开裂刚度代入式(1),即可获得组合板正、负弯矩区的等效刚度.
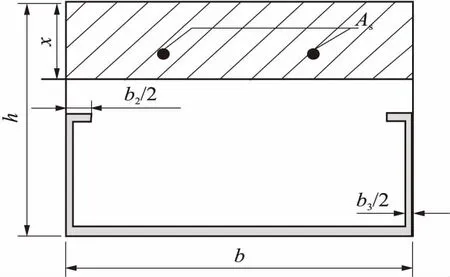
图10 换算截面计算图示
(1)
Mcr=γftkW0
(2)
式中:B为开裂构件等效截面的抗弯刚度;B0为全截面的抗弯刚度,B0=0.95EcI0,I0为全截面换算截面惯性矩;Bcr为开裂截面的抗弯刚度,Bcr=EcIcr,Icr为开裂截面换算截面惯性矩;Mcr为开裂弯矩;γ为构件受拉区混凝土塑性影响系数,γ=2S0/W0,S0为全截面换算截面重心轴以上部分面积对重心轴的面积矩;W0为换算截面抗裂边缘的弹性抵抗矩;ftk为混凝土轴心抗拉强度标准值.
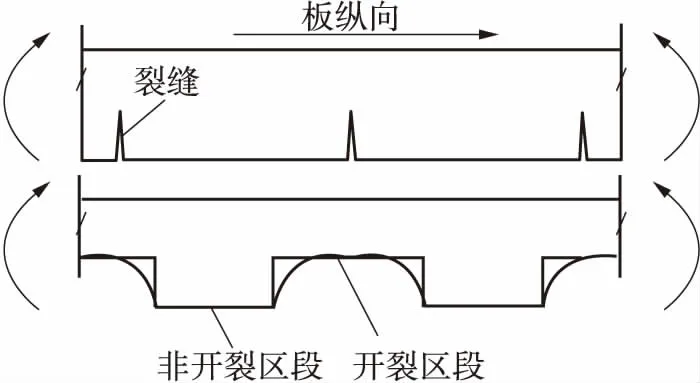
图11 混凝土开裂区域的刚度分布
对于连续梁,混凝土开裂后正、负弯矩区段的刚度均会发生变化,存在着梁的内力重分布.文献[11,15]的研究表明,可以使用共轭梁法确定连续梁的内力分布,其计算公式为式(3)、(4).为考虑开裂截面刚度的影响,这里使用等效刚度获取组合板的内力分布.
(3)
(4)
式中,B为正弯矩区等效刚度,P为所施加的荷载,l为计算跨径,M为跨中截面的弯矩,Mi为中支点截面的弯矩,Bi为负弯矩区段的等效刚度.
实际计算中,给定荷载P,然后联立式(1)-(4),不断调试中支点截面弯矩Mi使式(3)左右两边相等,从而确定连续板的内力分布以及正、负弯矩区的抗弯刚度.通过Maple软件对上述计算过程进行编程,可得到连续板正、负弯矩区的等效刚度,进而得到其内力分布.由此得到的荷载、支反力的试验值与理论值的对比如图9所示.
采用上述方法可以获得连续板的内力及刚度分布,之后就可按照经典梁理论计算连续板的变形.按上述方法得到的理论计算值和试验值的对比如表2所示,可以看出试验值和理论值吻合良好,因此可以采用上述方法进行变形计算.
3.2 负弯矩区裂缝宽度计算
GFRP混凝土-钢组合连续梁桥中支点负弯矩区的抗裂性也会影响该类结构的耐久性.目前,尚缺少针对GFRP-混凝土组合连续桥面板负弯矩区裂缝宽度的计算方法.文中尝试采用JTG D62—2004《公路钢筋混凝土及预应力混凝土桥涵设计规范》给出的钢筋混凝土梁裂缝宽度计算公式进行计算,计算公式如式(5)、(6)所示.其中,由于负弯矩区GFRP板对截面刚度的贡献很小,且试件的GFRP肋板及翼缘未进行界面处理,其对混凝土裂缝开展的约束效应较弱,因此受拉钢筋的配筋率计算时可忽略GFRP板的影响.
(5)
(6)
式中:C1为钢筋表面形状系数,对光面钢筋,C1=1.4;C2为作用长期效应影响系数,在此取C2=1.0;C3为与构件受力性质有关的系数,当为钢筋混凝土板式受弯构件时,C3=1.15;σss为钢筋应力;d为纵向受拉钢筋直径;ρ为纵向受拉钢筋的有效配筋率,当ρ<0.006时,取ρ=0.006;As为受拉区纵向钢筋截面面积;Ap为受拉区预应力面积;b为截面宽度;h0为截面有效高度;bf为受拉翼缘宽度;hf为受拉翼缘厚度.
图12为裂缝宽度实测值与按上述方法得到的计算值的对比.从图中可以看出,当裂缝宽度小于0.35 mm时,实测值与理论值较为接近,当超过0.35 mm后,由于负弯矩区钢筋屈服,实测值与理论值逐渐偏离,且越来越大.对图12中实测小于0.3 mm的裂缝宽度进行统计可得计算值与实测值的比值平均值为0.98,标准差为0.32,总计裂缝条数n=23.平均值、标准差与文献[16- 18]中钢筋混凝土裂缝宽度计算值的统计结果相当,说明了式(5)计算结果的可靠性.

图12 裂缝宽度计算值与实测值对比
表3给出了小于0.3 mm的裂缝宽度实测值与计算值的对比结果.从表中可以看出,wt/wm的均值为0.98±0.32,计算结果具有较大的离散性,这是由于混凝土材料的非均匀性、钢筋与混凝土间粘结应力的非均匀性等造成的[19].裂缝宽度较小时的离散性大于裂缝宽度较大时的离散性,这是由于当裂缝宽度较小时,采用规范的裂缝宽度计算方法离散性较大,估计是由开裂初期裂缝观测误差造成的;当裂缝宽度较大时,裂缝观测误差明显降低,试验值与理论值吻合较好.总体来看,裂缝宽度小于0.35 mm时可以采用式(5)计算GFRP-混凝土连续板负弯矩区混凝土表面的裂缝宽度.当裂缝宽度大于0.35 mm 后,负弯矩区钢筋开始屈服,组合板的负弯矩区进入塑性阶段,此时再计算裂缝宽度已失去工程意义.

表3 小于0.3 mm的裂缝宽度计算结果对比1)
采用式(5)的计算方法可对GFRP-混凝土连续板负弯矩区的裂缝宽度进行参数分析,以确定其在抗裂性方面的潜力.在此以80 kN时GFRP-混凝土连续板的裂缝宽度为例,说明负弯矩区裂缝宽度与配筋率的关系.图13为80 kN时LB-3试件的负弯矩区钢筋配筋率-裂缝宽度关系图,其中假定LB-3的截面尺寸、材料参数、钢筋类型、钢筋直径不变,改变负弯矩区的钢筋配筋率,由式(3)计算最大负弯矩截面的弯矩,然后用式(5)计算裂缝宽度.不难发现,当配筋率小于2.5%时,通过提高配筋率可以显著地限制负弯矩区的裂缝宽度,当配筋率大于2.5%以后,截面配筋率的提高对裂缝宽度的限制作用已不明显.因此,可以通过提高组合板负弯矩区钢筋的配筋率来降低裂缝宽度,以满足正常使用荷载下裂缝宽度的要求,必要时还可对GFRP-混凝土桥面板施加横桥向预应力,以提高负弯矩区的抗裂能力.
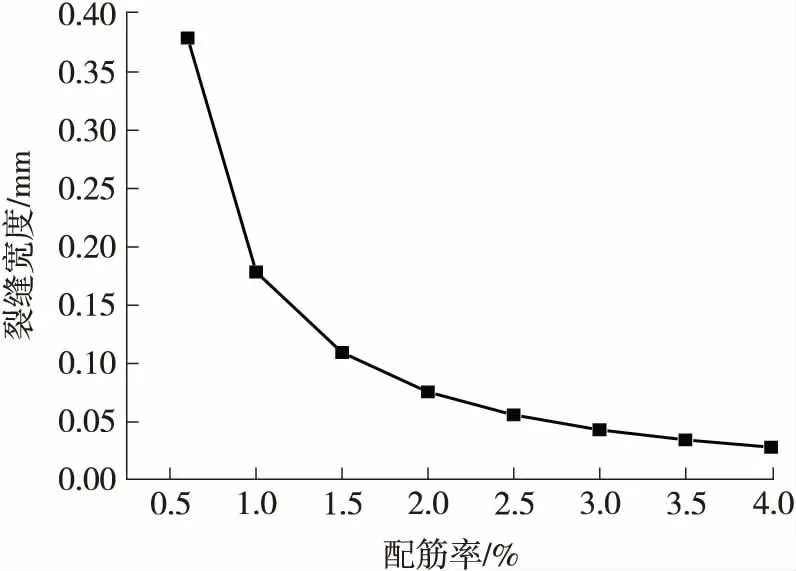
图13 80 kN荷载时LB- 3试件的配筋率-裂缝宽度关系图
4 结论
为提高钢-混凝土组合结构梁桥的耐久性,文中开展了GFRP-混凝土连续板的试验研究,探讨这种新型组合连续板结构的力学特性.基于前述试验研究和分析结果,得到如下结论:
(1)试验中的3个GFRP-混凝土连续板试件均发生了正弯矩区的弯剪破坏,卸载后连续板具有一定的变形恢复.试件破坏时板端无明显的界面滑移,说明试验中采用的湿粘结技术是一种有效的GFRP-混凝土界面连接形式.
(2)研究表明,现行规范JTG D62—2004中钢筋混凝土结构的等效刚度方法可用于计算混凝土开裂后GFRP-混凝土连续板的等效刚度,并可通过共轭梁法获得连续板的内力分布,最后通过经典梁理论计算GFRP-混凝土连续板的变形.
(3)由于GFRP肋板与混凝土的粘接较薄弱,且其距混凝土顶面较远,因而连续板负弯矩区的裂缝宽度主要与负弯矩区配筋率及钢筋应力有关.现行桥梁规范JTG D62—2004中给出的钢筋混凝土裂缝宽度计算方法可用于计算GFRP-混凝土连续板负弯矩区的裂缝宽度,计算精度是可以接受的.
(4)GFRP-混凝土连续板可作为一种新型桥面板用于钢-混凝土组合梁桥的桥面板结构,其破坏形态、承载力,刚度、抗裂性及裂缝宽度等力学性能均可以满足桥面板的受力要求.
:
[1] 黄侨,荣学亮,陆军.既有钢-混组合梁桥常见病害分析及其加固策略 [C]∥全国既有桥梁加固、改造与评价学术会议论文集.北京:人民交通出版社,2008:159- 164.
[2] KELLER T,SCHAUMANN E,VALLEE T.Flexural behavior of a hybrid FRP and lightweight concrete sandwich bridge deck [J].Composites Part A:Applied Science & Manufacturing,2007,38(3):879- 889.
[3] NELSON M,FAM A.Structural GFRP permanent forms with T-shape ribs for bridge decks supported by precast concrete girders [J].Journal of Bridge Engineering,2013,18(9):813- 826.
[4] AL-RAMAHEE M A,CHAN T,MACKIE K R,et al.Lightweight UHPC-FRP composite deck system [J].Journal of Bridge Engineering,2017,22(7):04017022.
[5] NOЁL M,FAM A.Design equations for concrete bridge decks with FRP stay-in-place structural forms [J].Journal of Composites for Construction,2016,20(5):04016024/1- 12.
[6] DIETER D A,DIETSCHE J S,BANK L C,et al.Concrete bridge decks constructed with fiber-reinforced polymer stay-in-place forms and grid reinforcing [J].Transportation Research Record Journal of the Transportation Research Board,2002,1814(1814):219- 226.
[7] ALAGUSUNDARAMOORTHY P,HARIK I E,CHOO C C.Structural behavior of FRP composite bridge deck pa-nels [J].Journal of Bridge Engineering,2006,11(4):384- 393.
[8] CHO K,PARK S Y,KIM S T,et al.Behavioral characte-ristics of precast FRP-concrete composite deck subjected to combined axial and flexural loads [J].Composites Part B Engineering,2013,44(1):679- 685.
[9] HALL J E,MOTTRAM J T.Combined FRP reinforcement and permanent formwork for concrete members [J].Journal of Composites for Construction,1998,2(2):78- 86.
[10] NELSON M,FAM A.Modeling of flexural behavior and punching shear of concrete bridge decks with FRP stay-in-place forms using the theory of plates [J].Journal of Engineering Mechanics,2014,140(12): 04014095.
[11] 黄辉,王文炜,戴建国.两跨连续GFRP-混凝土空心组合板受力性能试验研究 [J].建筑结构学报,2015,36(10):59- 65.
HUANG Hui,WANG Wenwei,DAI Jianguo,et al.Experimental study on structural performance of two-span continuous GFRP-concrete composite hollow slabs [J].Journal of Building Structures,2015,36(10):59- 65.
[12] 黄侨,佟兆杰.带翼缘槽型FRP板材-混凝土组合桥面板:CN104652267B [P].2016- 08- 17.
[13] PARK R,PAULAY T.Reinforced concrete and structures [M].New York:John Wiley & Sons,1975:48- 50.
[14] 公路钢筋混凝土及预应力混凝土桥涵设计规范:JTG D 62—2004 [S].
[15] 丁大钧,蒋永生.钢筋混凝土连续梁弯矩重分布全过程的计算 [J].冶金建筑,1982(2):14- 18.
DING Dajun,JIANG Yongsheng.Calculation of moment redistribution of reinforced concrete continuous beams [J].Metallurgy Building,1982(2):14- 18.
[16] 周建民,王眺,陈飞,等.高强钢筋混凝土梁裂缝宽度的试验研究和分析 [J].同济大学学报(自然科学版),2011,39(10):1420- 1425.
ZHOU Jianmin,WANG Tiao,CHEN Fei,et al.Research on crack-width of concrete beam reinforced with high-strength bars [J].Journal of Tongji University(Natural Science),2011,39(10):1420- 1425.
[17] 管俊峰,赵顺波,李晓克,等.钢筋混凝土梁裂缝宽度试验与计算方法 [J].中国公路学报,2011,24(5):74- 81.
GUAN Jun-feng,ZHAO Shun-bo,LI Xiao-ke,et al.Experiment and calculation method of crack width of reinforced concrete beams [J].China journal of highway and transport,2011,24(5):74- 81.
[18] 中国建筑科学研究院.钢筋混凝土结构设计与构造:85年设计规范背景资料汇编 [M].北京:中国建筑工业出版社,1985:188- 189.
[19] 过镇海,时旭东.钢筋混凝土原理和分析 [M].北京:清华大学出版社,2003:249.

