基于叶片摆振控制降低风机故障率
詹鹏,郭进学,陈晓明
(中国华电科工集团有限公司,北京 100160)
基于叶片摆振控制降低风机故障率
詹鹏,郭进学,陈晓明
(中国华电科工集团有限公司,北京 100160)
我国风电行业经过近年来迅速增长,伴随着大量风电机组出质保期,风电机组运维日趋迫切,叶片摆振是造成风电机组故障的主要原因之一。针对风机运维中遇到的叶片摆振问题,提出了最小最大线性二次型高斯最优控制方法。该方法应用欧拉-拉格朗日方程对风机叶片的振动系统建立数学模型,并设计最小最大LQG控制器。仿真结果显示:控制器对叶片的摆振有很好的控制作用,达到了降低风电机组故障率、提高风电机组发电效率的目的。
风电机组;风机叶片;摆振;故障率;仿真研究
0 引言
随着能源危机和环境污染问题的日趋严重,风能作为绿色能源已受到世界各国的普遍关注。我国风电行业也在近10年内迅速增长,2015年国内风电新增装机容量达到30.5 GW,根据国家能源局2020年能源需求预测的基准方案,2015—2020年5年内的风机装机容量目标是210.0 GW,平均每年新增装机42.0 GW,年均复合增速10.9%。
然而在风电迅猛发展的同时,风电场的建设和全生命周期管理尚处于初级探索阶段,其中风电场运行维护在风电场全生命周期中占时最长,并且运行维护过程中产生的数据既可以回馈风场的设计阶段,也可以为风电场决策提供必要的数据。在风电场运行维护(以下简称运维)过程中,风力发电机组会遇到不同部件或者不同类型的故障,其中叶片系统的故障占到全故障情况的13.4%[1],而引起叶片故障的主要原因之一是叶片的振动问题。所以,风机叶片系统的振动控制问题受到学者的普遍关注[2-4],提出了几种用于风机叶片振动的控制方法。
本文主要针对叶片摆振问题建立风机叶片系统在旋转情况下的运动模型,并且考虑有限维模型代替无限维模型引起的不确定性,应用最小最大LQG方法对降阶后的系统模型设计控制器,从而解决叶片的摆振控制问题。
1 系统建模和不确定性建模
1.1 叶片建模
图1是风机叶片的简单示意图,图中:yj(x,t)为叶片j在摆振方向的位移;Ψj(t)代表叶片j的方位角。在建模过程中,风机叶片被看作长度为L,线密度为ρl,并且以Ω的固定角速度旋转的伯努利-欧拉梁。叶片j的方位角在t时间为
(1)
式中:Ψ1(t)=Ωt,j=1,2,3。
根据伯努利-欧拉梁的运动方程[5]
(2)
式中:EI为弯曲刚度;I为截面惯性矩;c为应变阻尼系数;ρl为线密度;A为横截面积。
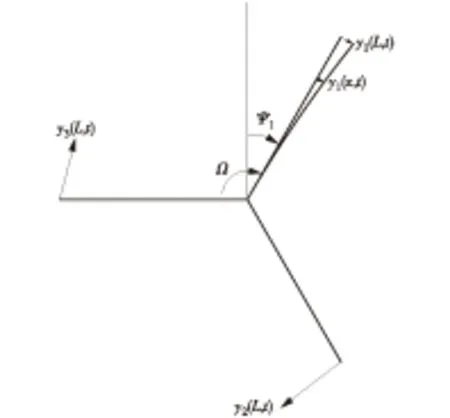
图1 叶片摆振方向模型
根据式(2)可以得到叶片上的x点在时间t的摆振位移表达式
(3)
式中:Φi(x)为叶片的振型表达式;qji(t)为叶片的自然模态。
引入欧拉-拉格朗日方程
(4)

表1 NREL5-MK沿海风机叶片参数[7]
式中:T和V分别代表系统的动能和势能;Qi代表作用在系统上的广义非耗散力Q(t)的第i阶分量。
将系统的动能和势能代入式(4)可以得到拥有3n个自由度的风机叶片系统的摆振运动方程
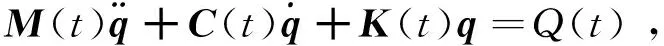
(5)
式中:矩阵M,C,K∈R3n分别为广义质量矩阵、广义阻尼矩阵和广义刚度矩阵;q为系统的广义坐标向量。
在风机叶片系统的运动方程中,含有一个与时间相关的周期项:叶片的方位角。但是经典的时不变分析和控制原理对于含有周期运动的系统并不适用。为了解决这个问题,必须将时变系统转换为时不变系统,所以引进多叶片坐标变换,也就是科尔曼变换[5-6]。
根据科尔曼变换,最终将时变系统(5)转换成以下的时不变系统,即将旋转平面坐标系转换成非旋转平面坐标系。
(6)
式中:qnr和Qc分别表示非旋转平面的广义坐标向量和非耗散力。
为了将上述运动方程转换成状态空间的形式引进状态向量
(7)
得到风机叶片系统摆振模型的状态空间形式
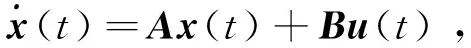
(8)
式中:
(9)
控制向量u(t)对应着施加在每个叶片顶端的力,被定义为
(10)
再根据上面给出的摆振位移表达式(3),可以得到叶片的摆振位移输出表达式
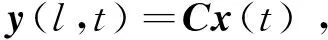
(11)
式中:
(12)
所以,最终的状态空间形式的系统模型由式(8)和(11)表示。可以看出,该系统是一个无限维系模型,控制这样的系统会使得运算复杂度和控制器负载巨大。为了解决这个问题,将系统降阶,取n=1得到一个低维的系统模型。本文采用叶片(型号为LM61.5P2)进行试验仿真,表1列出了叶片的基本参数,文献[7]提供了该型号叶片的详细信息,叶片的振型公式和自然频率由文献[8]提供的软件计算得到。将叶片参数代入系统得到作用在叶片上的作用力和顶端位移的传递函数。
Gdis(s)= (-3.331e8s5+7 364s4+506.5s3+
7.912e5s2+3.469e4s+1.879e7)/
(s6+0.137 6s5+159.1s4+14.83s3+
8 101s2+376.6s+1.317e5) 。
(13)
为了使位移信号便于处理,需调整传递函数的增益,在其中加入一个放大器K,因此最后系统的传递函数为
(14)
式中:K=106。
1.2 不确定性建模
在引言中提到,本文将应用最小最大LQG方法对叶片摆振进行控制,而该方法是基于不确定系统的。风机叶片摆振模型的状态空间方程是一个无限维的系统,应考虑将一个有限维的系统代替该无限维系统而带来的不确定性。系统的真实传递函数可以表示为
(15)
式中:G1(s)由式(14)定义;W(s)是系统的权函数;Δ(s)是一个不确定传递函数,它要满足
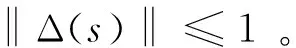
(16)
在最小最大LQG鲁棒控制器的设计过程中,权函数W(s)是一个重要环节。权函数选取的好坏直接影响系统控制性能和系统的鲁棒性,根据Doyle 的经典文献[9],可以计算得到权函数。
系统的权函数表达式为
W(s)= (2 000s4+5 749s3+8 262s2+6 956s+
2928)/(1.464s4+28.4s3+400.4s2+ 1 889s+14 28e4) 。
(17)
2 最小最大LQG控制
本文的主要内容是利用最小最大LQG方法解决风机叶片系统的摆振问题,在这一节简要介绍Ugrinnovskii和Petersen关于无限时间的最小最大LQG控制问题[10]。首先考虑以下形式的随机不确定系统
(18)
式中:u(t)是控制输入;W(t)是扰动输入对应的高斯白噪声过程;ξ(t)是不确定输入;z(t)为不确定输出;y(t)是测量输入。
在系统(18)中,不确定输入ξ(t)是由不确定输出z(t)通过不确定动态产生的,二者的关系必须满足
式中:d是一个给定的常数。
系统(18) 的不确定描述式(19) 对应着满足H∞范数边界(16)的不确定传递函数Δ(s),也就是说满足H∞范数边界能保证满足随机不确定约束(19)。 因此,第1节的数学模型(8)和(11)可以转换成系统(18) 的形式。
考虑以下形式的代价函数
式中:R≥0,G≥0。
最小最大LQG控制算法设计的控制器目的是使得代价函数(20)的最大值最小化,而代价函数的最大值对应着满足不确定约束(19)的所有不确定系统中的最大值,也就是该算法能使系统在最坏情况下代价函数的值实现最小化。
通过以下方程建立最小最大LQG控制器:
(21)
其代价函数对应的上界为
为了设计控制器,参数τ必须使得Wτ最小,而这个最优值τ则对应着由式(21)定义的最优控制器。
3 仿真结果
本文通过Matlab软件仿真得到试验结果,模型数据来自于NREL的近海5MW风机叶片。
3.1 气动负载

(23)
3.2 控制结果
将叶片振动位移系统
(24)
转换成式(18)的形式。需满足D2D2′>0的条件,设D2=0.01。代价函数(19) 中的参数d决定系统的不确定性扰动信号的概率分布,设定d=10-6。代价函数中的矩阵R=C2′,也即x(t)′Rx(t)表示系统输出的范数平方;而u(t)′Ru(t)项表示控制器的增益,设定G=10-8。
为了设计控制器,必须找到使得Wτ最小的参数τ,最后得到最优参数
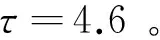
通过式(21)构建控制器,将其加入系统,得到叶片1的叶片位移控制效果。图2是控制后和未控制的叶片位移,可以看出,加了控制器后的系统振动幅度和频率明显减小,未控制的振动的最大位移接近2m而加入控制之后最大振动位移只有1m不到。
图3是将位移信号傅里叶变换之后的频谱图,可以看出,在叶片旋转频率(0.2Hz) 和叶片的1,2阶自然频率处施加控制后得到了很大的改善,3个峰值都被很好地抑制,所以,控制器在针对叶片的低频振动部分有很好的控制效果,而低频部分正是叶片摆振的主要影响因素。可以看出,本文的控制器对叶片摆振有很好的控制效果。
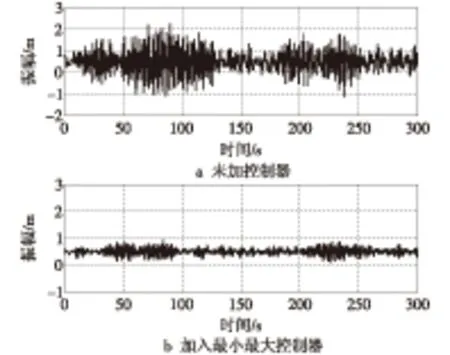
图2 控制效果
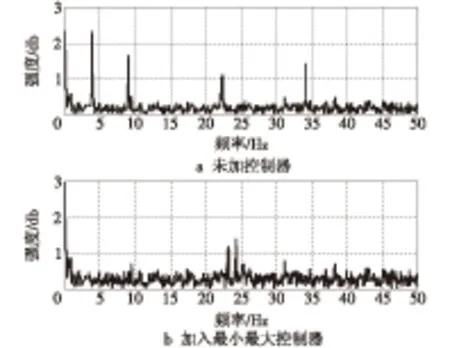
图3 摆振位移频谱
4 结论
我国风电装机容量逐年加大,对风电机组的运行维护提出了更高的要求。风机叶片系统故障在风机所有故障情况占13.4%,是一种占比较大的故障类型。本文针对风机叶片振动进行控制,进而降低风机故障率,达到提高风机发电效率的目的。
仿真试验表明,对叶片施加控制后,叶片振动幅度有了大幅度的降低,低频振动也得到了有效的控制。通过这种方法可以减少由于风机叶片振动引发
的风机故障,预计降低风机故障率5%,提高风电机组发电效率。
[1]孙鲜明.复杂工况下风力发电机组关键部件故障分析与诊断研究[D].沈阳:沈阳工业大学,2014.
[2]RICE J K,VERHAEGEN M.Robust and distributed control of a smart blade[J].Wind energy,2010,13(2):103-116.
[3]STAINO A,BASU B,NIELSEN S R K.Actuator control of edgewise vibrations in wind turbine blades[J].Journal of sound and vibration,2012,331(6):1233-1256.
[4]SVENDSEN M N, KRENK S, HOGSBERG J.Resonant vibration control of rotating beams[J]. Journal of sound and vibration,2011,330(9):1877-1890.
[5]GAWRONSKI W K.Advanced structural dynamics and active control of structures[M].New York:Springer,2004.
[6]HANSEN M H.Improved modal dynamics of wind turbines to avoid stall-induced vibrations[J]. Wind energy,2003,6(2),179-195.
[7]JONKMAN J,BUTTERFIELD S,MUSIAL W,et al. Definition of a 5 MW reference wind turbine for offshore system development[R].Colorado:National Renewable Energy Laboratory, Technical Report,2009,NREL/TP-500-38060.
[8]BUHL M. A simple mode-shape generator for both towers and rotating blades.[CP].(2014-09-28) [2017-03-31]. https://nwtc.nrel.gov/Modes.
[9]DOYLE J C, FRANCIS B A, TANNENBAUM A R. Feedback control theory[M].New York:Macmillan,1992.
[10]ZHANG Yuhong, AGRAWAL S K, POTA H R, et al. Minimax linear quadratic gaussian control of longitudinal vibration for cable transporter systems with multiplicative nonparametric uncertainties[J].International journal of acoustics and vibration,2005,10(3):137-143.
(本文责编:白银雷)
2017-02-10;
2017-03-30
TK 83
B
1674-1951(2017)04-0015-04
詹鹏(1991—),男,江西九江人,工程师,从事风电机组振动诊断及故障分析方面的研究工作(E-mail:zhanp@chec.com.cn)。

