天线时域平面近场测试的误差分析
曹猛 薛正辉 任武 李伟明 朱若晴 蔡洪伟
(北京理工大学信息与电子学院, 北京100081)
天线时域平面近场测试的误差分析
曹猛 薛正辉 任武 李伟明 朱若晴 蔡洪伟
(北京理工大学信息与电子学院, 北京100081)
天线时域近场测试技术对误差体系研究的缺失,导致测试结果的不确定度分析一直无法完成.为解决这一问题,以天线时域平面近场测试为例,对时域近场测试的误差进行研究,给出时域测试区别于频域测试技术的四个误差项:探头调制误差、信号源稳定度误差、时间采样间隔误差、时间采样长度误差.在给出误差项后,对误差的产生机理进行了讨论,通过仿真和实测给出了误差对测试结果的影响.
时域;近场测试;误差分析;不确定度分析
DOI 10.13443/j.cjors.2017011002
引 言
近场测试因其保密性高、测试距离短等优点在天线测试中被广泛应用.频域近场测试最早出现于20世纪50年代,在加入了近场测试的探头误差修正后,测试结果的精度有了质的飞跃,近场测试技术开始被广泛应用.
该项技术被大规模应用还有一个很重要的原因是因为频域近场测试可以对测试结果进行不确定度的估计,估计的主要核心内容是对频域近场测试包含的所有误差项的产生机理、误差的评估方式、误差对测试结果的影响即结果的不确定度进行分析.Yaghjian首先给出了天线平面近场测试的误差上限分析[1],Newell和Crawford在20世纪80年代对频域近场测试完成了误差项不确定度的分析,使得频域近场测试技术达到了实际应用的水平[2].IEEE对天线近场测试给出了相关的测试标准和不确定度的计算标准[3],对频域近场测试的误差项也有很多文章进行分析及修正[4-6].但频域近场测试由于是单点频测试,在进行宽频带多频点和大口面天线测试时的效率很低,同时频域测试是稳态测试,对雷达等系统来说需要进行瞬态的分析,因此对时域测试的需求开始出现.
时域近场测试理论最早在1994年由Hansen提出,最初的文章给出了声学场和电磁场的宽频带时域测试理论,在1995年又给出了带有探头修正的时域近远场变换,完善了时域近场测试理论[7-9].此后国内外出现了时域近场测试的研究热潮,针对时域测试系统实现方式、应用方向和部分误差进行了研究[10-14].对时域近场测试技术的应用都是在采集时域信号后进行傅里叶变换得到频域的信息最后得到频域的远场区方向图,对待测天线的纯时域特性的测试很少.时域近场测试技术采用时频域相结合的方法,但想要达到频域测试的工程应用水平还是缺少很重要的参考项:误差项研究和测试结果的不确定度分析.时域近场测试现在很重要的一个问题就是缺少对时域与频域测试误差项之间的相同点与不同点的归纳以及对时域近场测试技术的误差项的系统总结.
Newell和Crawford总结了频域近场测试中的18项误差,总体而言分为两大部分:由于探头自身的参数导致的误差和在测试过程中信号接收和空间谱计算出现的误差.在时域近场测试中,误差也可分为这两大部分,但是两个部分中的具体误差项有所差别,本文给出了对两部分误差项的分析.
本文针对时域平面近场测试技术进行误差分析.首先介绍了时域近场测试系统构成,然后给出了时域区别于频域测试技术的误差项,最后对误差项进行了具体的分析.具体来说,时域近场测试技术在具有频域测试技术的误差项外,还有四个独有误差项:探头调制误差、信号源稳定度误差、时间采样间隔误差、时间采样长度误差.在给出独有误差项后,分别从误差产生原因和误差对测试结果的影响对误差进行分析.
1 天线时域平面近场测试误差
时域平面近场测试系统如图1所示,时域信号源作为激励,时域激励信号分为两路:一路经由待测天线发出,探头在采样平面上进行采样,最后由采样示波器进行实时采样;另一路时域信号直接连接采样示波器,作为采样触发信号及误差修正的参考信号.
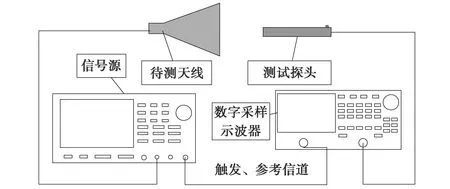
图1 天线时域平面近场测试系统
由图1可以看到,时域系统与频域系统最大的区别就是信号源与采样示波器代替了矢量网络分析仪,时域信号源的信号稳定度与频域信号相比较弱,所以时域信号源稳定度误差是时域测试一项很重要的误差项.时域测试采用时域信号,因此采样信号与时间相关的误差是时域平面测试独有误差项.在实际测试中探头采样得到的信号发生明显的变化,所以探头对信号的调制也是一个时域测试中出现的新误差项.
在进行时域近场测试误差项的总结前,需要先给出误差项分析的前提[3]74:
1) 所有近场测试的理论是准确的,对误差的评估计算在理想情况下进行.
2) 所有数值计算中因为计算精度导致的误差不进行分析,比如近远场变换时计算精度的误差不进行分析.在时域测试中,此类误差还包括进行时频域变换时的计算精度导致的误差.
3) 假设每一个误差项都是独立的,与其他误差是不相关的.
4) 每一项误差都会在测量和远场参数的计算过程中产生对应的误差.
5) 在对由误差项导致的测试结果的误差进行分析时,可以不与真实的天线结果作对比,而是与一个假定不受其他误差影响的结果作对比.
以上是对误差进行机理分析和对结果影响估计的一些基本原则,在以上几个前提下,频域近场测试给出了18项误差.从前面对时域测试系统的分析可以看出时域平面测试自身还有独有的误差项.这些独有误差项包括由于探头自身特性导致的误差项及三项测试导致的误差项.
时域近场测试中探头自身特性导致的误差项与频域中的误差项有联系但又不完全一致,在频域中探头的误差项主要分为以下几部分:探头方向图、探头极化轴比、探头增益等,误差对应单一频点.Newell在文献[2]中给出了探头频域误差分析的推导和误差上限估计.时域近场测试中这些误差项同样存在,只是对误差项的描述方式略有不同.由于时域信号的宽频带特性,时域信号可以认为是包含了工作频带内所有频点的信息,所以探头的误差项都变为了对应频带内所有频点的误差项.除了频域中已给出的误差项外,探头在时域中还有新的需要考虑的误差——探头调制误差.
时域近场测试导致的误差包括以下误差项:信号源稳定度误差、时间采样间隔误差、时间采样长度误差.因为时域测试的激励信号是一个持续时间很短的高斯信号,信号的幅值和触发时间在每一次激励时都会有变化,每一次的信号变化都是独立的,时域信号的幅值和相位的稳定度都要远远低于频域测试的激励信号,所以在时域测试中时域激励信号的幅值和触发时间还有脉宽会对测试结果产生影响,而这三项误差组成了信号源稳定度误差.时间采样间隔误差也是时域测试的独有误差,在频域测试中采样点的空间采样间隔需要满足奈奎斯特采样定律,采样间隔要小于最小波长的一半,而在时域测试中,对信号的采样间隔也需要满足奈奎斯特采样定律,时间的采样间隔要小于最高采样频率倒数的一半,或者说信号采样率(时间采样间隔的倒数)要大于采样频率的二倍,否则采样信号的频谱会发生混叠.三项误差的最后一项误差是时间采样长度误差.因为时域激励信号是周期信号,通过触发信号控制采样示波器进行信号采集,如果采样信号时间过长会导致采集到下一周期的信号,而如果采样时间过短会导致信号采集不完整,过长或过短都会影响时域信号完成度和信号的频域信息.
2 误差机理研究及结果影响分析
2.1 探头调制误差
探头作为近场测试的信号采集工具,探头误差对测试结果的影响是所有误差项中最大的,而所有探头误差中最重要的就是探头的方向图误差.由于近场测试的探头不是一个理想点源,接收到的能量强度会受到自身空间接收能力的限制,所以频域近场测试对探头的修正主要就是对方向图的修正.
频域近场测量的探头修正首先要得到探头的方向图逆接收特性,然后再对空间谱进行修正,从而达到修正探头误差的目的.探头的逆接收特性表达式为[9]573
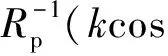
(1)
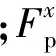
从式(1)可以看出频域对探头的修正就是方向图的修正,但是在时域近场测试中,除了方向图误差外,由于宽频带特性、波导同轴转换匹配、探头传递函数导致的信号变形等方面的影响也需要考虑.其中在宽频带测试条件下由于探头传递函数导致信号发生变形的误差可以认为是探头对接收信号进行了调制,因此可以定义为探头调制误差.
首先是探头的波导同轴转换匹配,由于探头对不同频点驻波是不一致的,所以会对信号造成一定的影响,在时域上的直接表现就是信号会发生变形.但是Newell认为在测试中,探头的阻抗在所有频带范围内都认为是固定的50 Ω,工作频带内的所有频点都是理想的阻抗匹配,否则无法继续进行分析,所以工作频带内不会出现因为端口的反射系数不同而导致接收信号出现误差.在实际测试中,可以采用驻波较好的探头,这样在能量损失很小的情况下信号的变形可以忽略不计.
时域近场测试最重要的误差项就是探头对接收信号的调制误差.由于探头有自身的系统响应,所以一个时域信号进入探头后会与探头的系统响应函数进行卷积最后在端口输出,因此得到的采样信号会发生变形,最终影响时域方向图的计算结果.
根据波导的相关理论[15]63可以得到开口波导探头在频域时的传递函数为
Swg=e-γz=e-(αc+αd+jβ)·d.
(2)
式中:γ为传播常数;αc为波导壁所引起的导体衰减常数;αd为由波导中填充介质所引起的介质衰减常数;β为相位常数,是信号相位的变化量;d为波导探头长度.根据αc、αd和β的定义[16]将这几项展开后得到传递函数具体表达式为
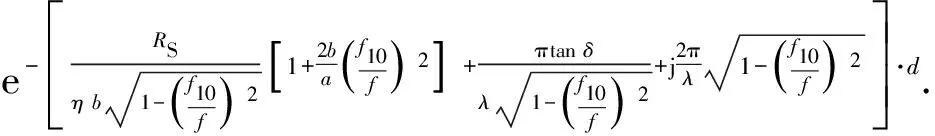
(3)
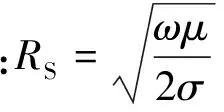
探头调制误差对采集信号造成的影响可以通过仿真得到.仿真结果如图2所示,图2(a)为输入信号,是一个工作频段为2~5 GHz的调制高斯信号,对一个S波段标准喇叭进行激励.图2(b)分别为理想探针得到的信号和波导探头采集到的信号,可以看到因为探头的调制,信号发生了变形.图2(c)给出了两种采样方式采集到的信号的频谱.可以看到两种情况的频谱只有幅值略有不同,工作频带没有变化.由于波导是一个无源器件,信号在相同频点的幅值的衰减(以dB为单位)和相位的变化都是一致的.将信号变换到频域后,信号与频域近场测试得到的信号没有区别,这也是时域近场测试技术可以采用时频域结合的办法进行近远场变换和计算的原因.
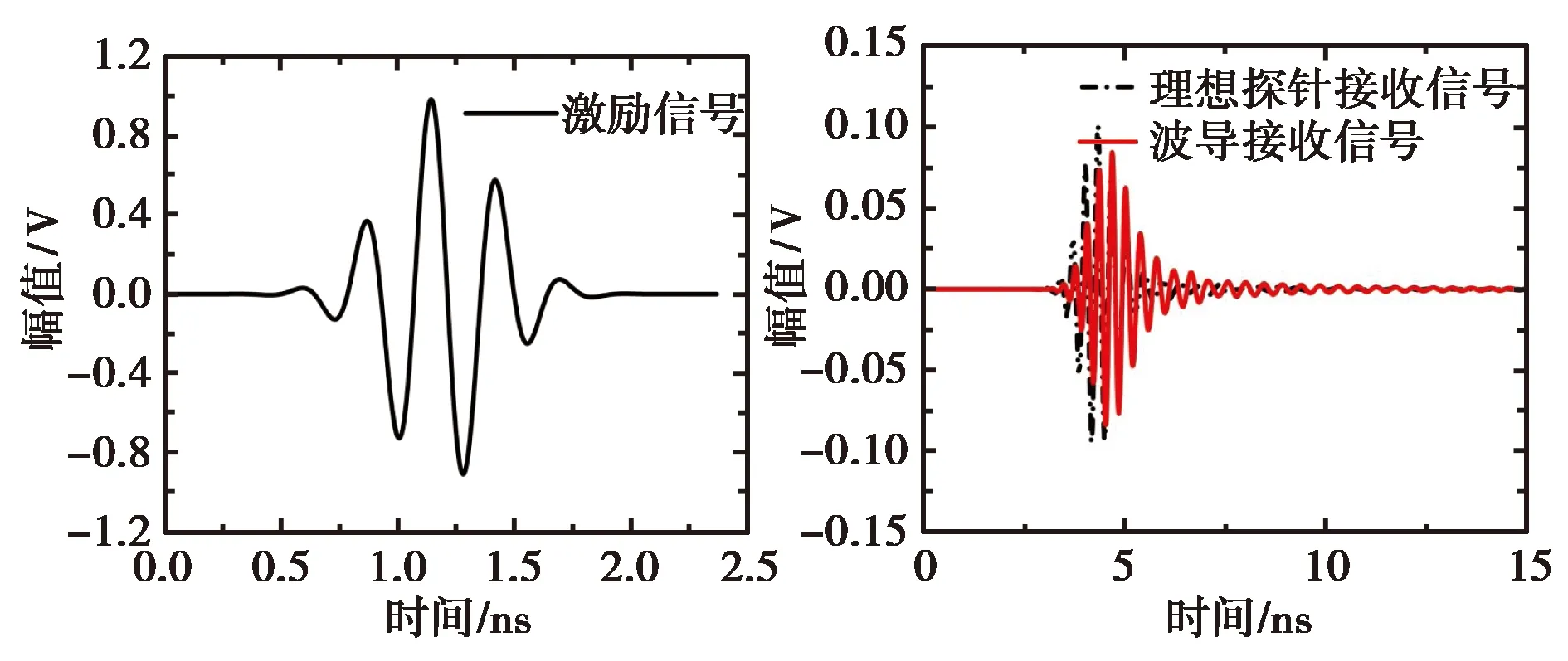
(a) 激励信号 (b) 接收信号对比
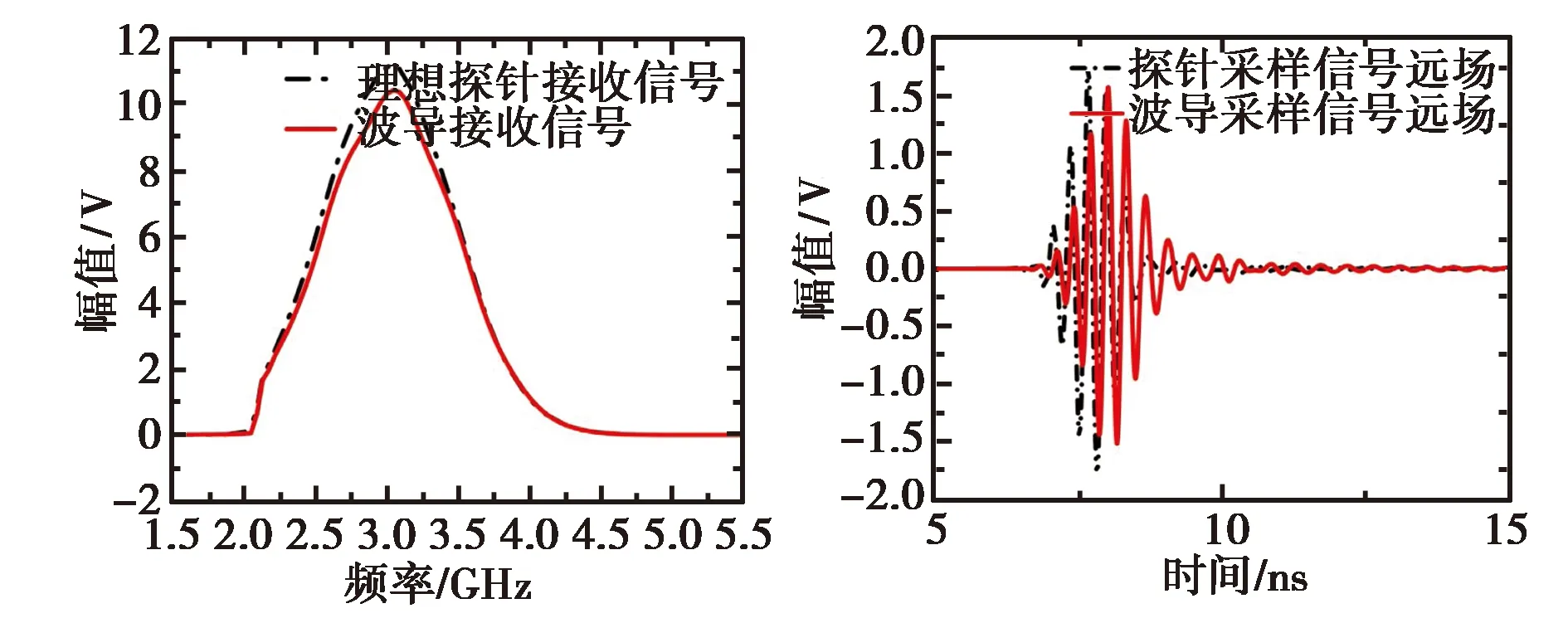
(c) 接收信号品频谱 (d) 远场区时域信号对比图2 波导调制误差
从频域角度分析,频域信号的幅值相位会发生变化,但是因为频域测试是针对单频点的测试,同一频点信号的幅值相位在同一个边界条件中的变化是相同的;而时域信号在频域上是多个离散频点的组合,首先探头要在频域上对信号进行截断,只允许工作频段内的信号通过,然后由于相速度不同,导致信号的色散,变换到时域上就是信号变形.而从时域角度分析,信号传播的边界条件及模式发生变化后的表现就是信号被调制后发生变形,信号的辐射功率在不考虑损耗的情况下不变,但是信号的持续时间与信号的峰峰值都会发生变化.这样的变化在变换到频域计算时不会有影响,但是对时域测试来说,信号的持续时间是一个很重要的测试指标,因为它可以表征待测天线的口面能量达到稳态的时间;同时如果不将波导的调制解调出去的话,表征待测天线的辐射能力的时域方向图会出现极大误差.图2(d)给出了图2(b)中两种采样信号计算得到的远场区(θ=0,φ=0)点处时域波形,可以看到利用探头采样信号计算得到的时域远场波形与理想情况下的时域远场波形有很明显的区别,远场波形的峰峰值差值达到了0.25 V,波形持续时间差值为0.53 ns.由对比可以看出探头调制误差会导致计算结果的误差.
下面给出S波段标准喇叭天线在同一时刻的采样平面的瞬时电场分布,利用最高工作频率为12 GHz的高斯脉冲对喇叭进行激励.图3(a)为理想情况下的近场能量分布,图3(b)为波导探头采样得到的近场能量分布.
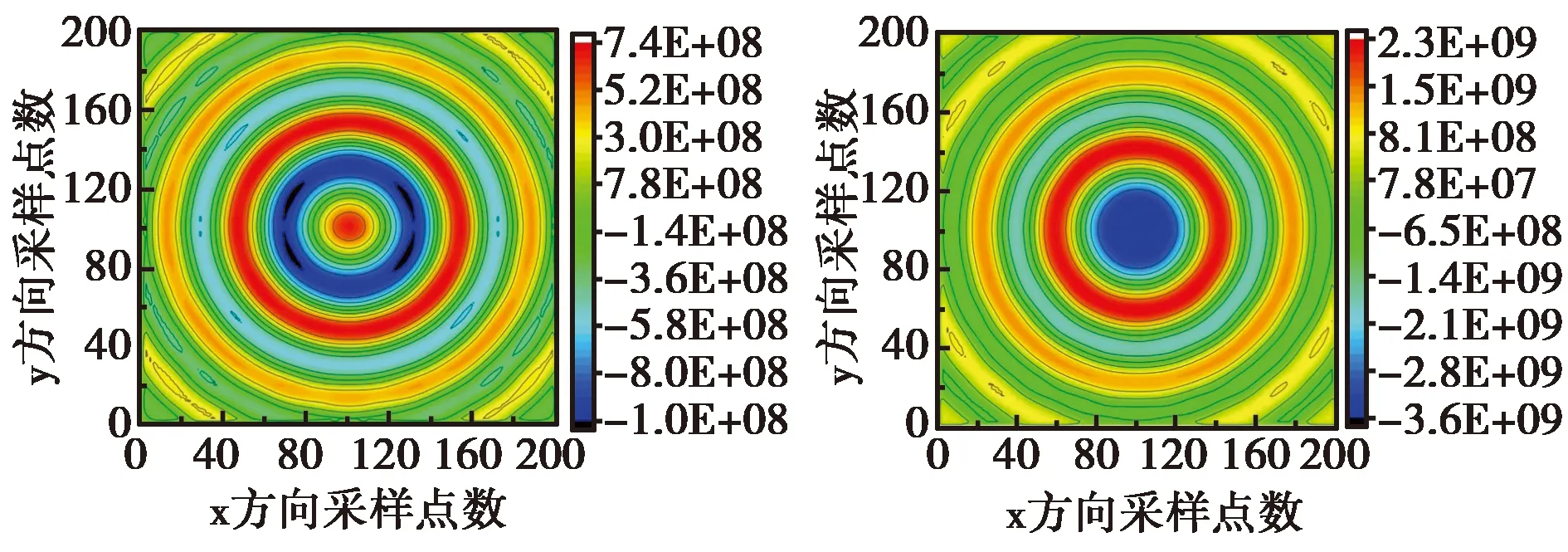
(a) 理想情况 (b) 波导探头图3 时域信号在近场采样面瞬时能量分布
通过瞬时的能量分布对比可以看出无论是能量幅值的数量级还是能量分布都有很大区别,场强的差值达到了4.16×109V/m.理想情况的场值有两个明显的波峰,采样面正中是波峰;探头采样得到的场值只有一个明显的波峰,采样面正中是波谷.这样的误差会对时域的远场区方向图的结果造成影响.
2.2 信号源稳定度误差
信号稳定度的误差可以归纳为两部分原因:激励信号源的不稳定及采样设备的不稳定.首先时域近场测试采用的信号源大多是脉冲发生器,通过晶体振荡产生得到的是一个近似的高斯脉冲信号,因为这是一个脉冲信号,所以这种信号的稳定度远远低于稳态的频域信号,同时由于信号源要在极限工作状态运转,信号的幅值、脉宽和触发时间都会变得不稳定,在信号源工作较长时间后这种误差会非常大,这样会造成接收信号的变形,严重地影响测试结果.另外,为了对信号进行修正,需要建立信号源与采样设备之间的参考信道,根据参考信道得到的信号来进行修正,对采样接收设备来说,即使输入相同的信号,接收到的信号也会由于各项误差发生变化,这两个方面的误差组合起来就是信号的稳定度误差.
由于对采样信号和激励信号是同时采集的,这样激励信号的变化和采样设备的误差可以通过对参考信道的激励信号的修正来完成对采样信号的修正.这是对时域采样信号进行信号源不稳定造成的误差修正的前提.
下面以高斯脉冲源为例进行信号源稳定度的误差分析.高斯信号的表达式为
g(t)=Ate-4t2/τ2+tr.
(4)
式中:At是信号的幅值;tr是信号的触发时间;τ是信号的脉宽.信号源误差分别为A't、Δtr、τ',其中A't=At+ΔA,ΔA为幅值变化量,τ'=τ+Δτ.
在这一节里,将对激励信号的峰值、脉宽和触发时间进行分析,进而显示出信号源误差对测试的影响.图4给出了不同情况下激励信号和接收信号的变化.
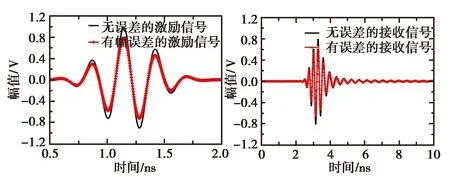
(a) 幅值误差
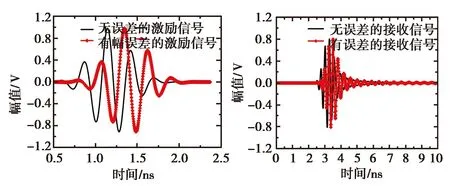
(b) 触发时间误差
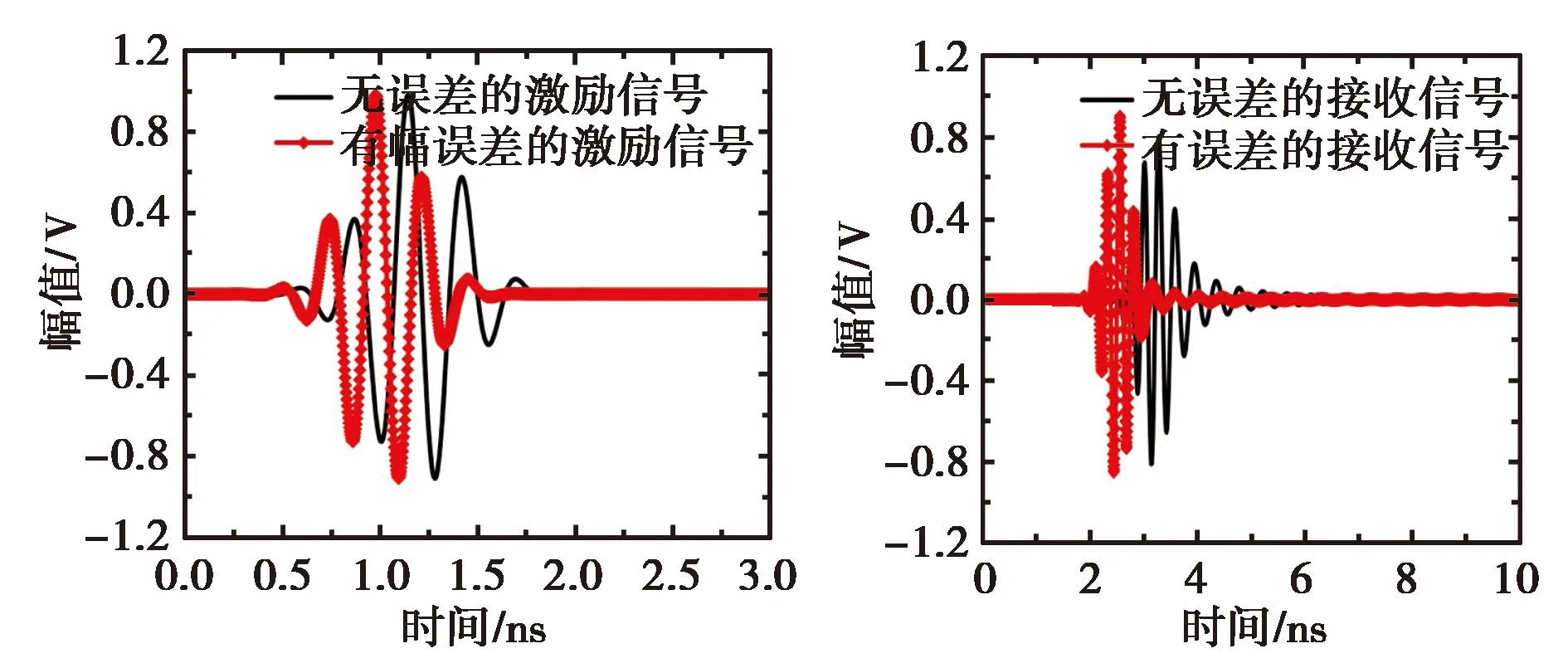
(c) 信号脉宽误差图4 信号源误差对激励信号及接收信号的影响
从图4的结果可以看出:信号源的幅值改变会造成接收信号的幅值改变,接收信号的变化与信号源的变化成正比;信号源触发时间的变化则会影响接收信号的触发时间;而信号源脉宽的变化会导致接收信号发生变形,两者的变化量之间不是简单的比值关系.时域信号的幅值和触发时间分别对应了频域信号的幅值和相位,脉宽改变会改变信号的工作频带,而信号源的这三个误差都会极大影响信号的准确性,进而严重影响最后的测试结果.
图5给出了实际测试中信号源误差对方向图的影响.待测天线为S波段标准喇叭,采样面边长为1 089.6mm,采样间隔为22.7mm,探头与待测天线之间距离为350mm,激励信号与图2(a)中高斯调制信号一致,信号源信号的峰峰值为20V,信号宽度为1.5ns,信号源幅值误差最大值为4V,信号宽度误差最大值为0.03ns,触发时间误差最大为0.2ns.图5(a)分别给出信号源误差修正前后的3.3GHz频率处的E面远场区方向图和待测天线的远场测试得到的相应频率的远场方向图.图5(b)分别给出了两种方向图与远场测试方向图的差值.由图5(a)可以看出在置信角域内(±40°左右),对信号源误差进行修正后方向图与远场测试得到的方向图拟合很好,而误差未修正前计算得到的方向图主瓣指向与副瓣都发生了很明显的变化,主瓣与远场测试结果的主瓣近似,而副瓣则完全不一致.由图5(b)可以看出修正后方向图与远场测试方向图的差值在置信角域内最大值为0.4dBm,而未修正方向图的差值最大值可以达到9.6dBm.误差修正后的方向图副瓣电平误差主要来源于探头对准和探头采样位置等误差,这些误差带来了方向图的误差.
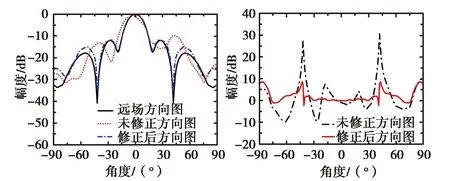
(a) 方向图计算结果 (b) 方向图差值图5 信号源误差对方向图的影响
2.3 时间采样间隔误差
时域测试的时间采样间隔误差包含两类误差:第一类是指在对时域信号进行采集时所采用的时间采样间隔的选取,第二类是指对时域信号进行采样时由于仪器自身误差导致的采样点的漂移.
第一类误差是时域测试独有的误差,是在某一空间采样点上进行时域采样时的时间步长,即采样示波器的采样间隔.在频域测试中,空间采样间隔要小于奈奎斯特的抽样间隔(NyquistSamplingInterval)即Δλ≤1/(2λmin).而在时域测试中,除了空间采样间隔需要继续遵循这一原则外,时间的采样间隔即信号的分辨率也要进行考虑.根据用信号样本表示连续时间信号的抽样定理, 应小于奈奎斯特抽样间隔,即Δt≤1/(2fmax),其中fmax为测试频带的最高频率.这样将采集得到的时域信号进行频域频谱分析时,不会出现频谱重叠,没有混叠误差存在.而当时间采样间隔过大时就会发生频谱重叠,产生混叠误差.
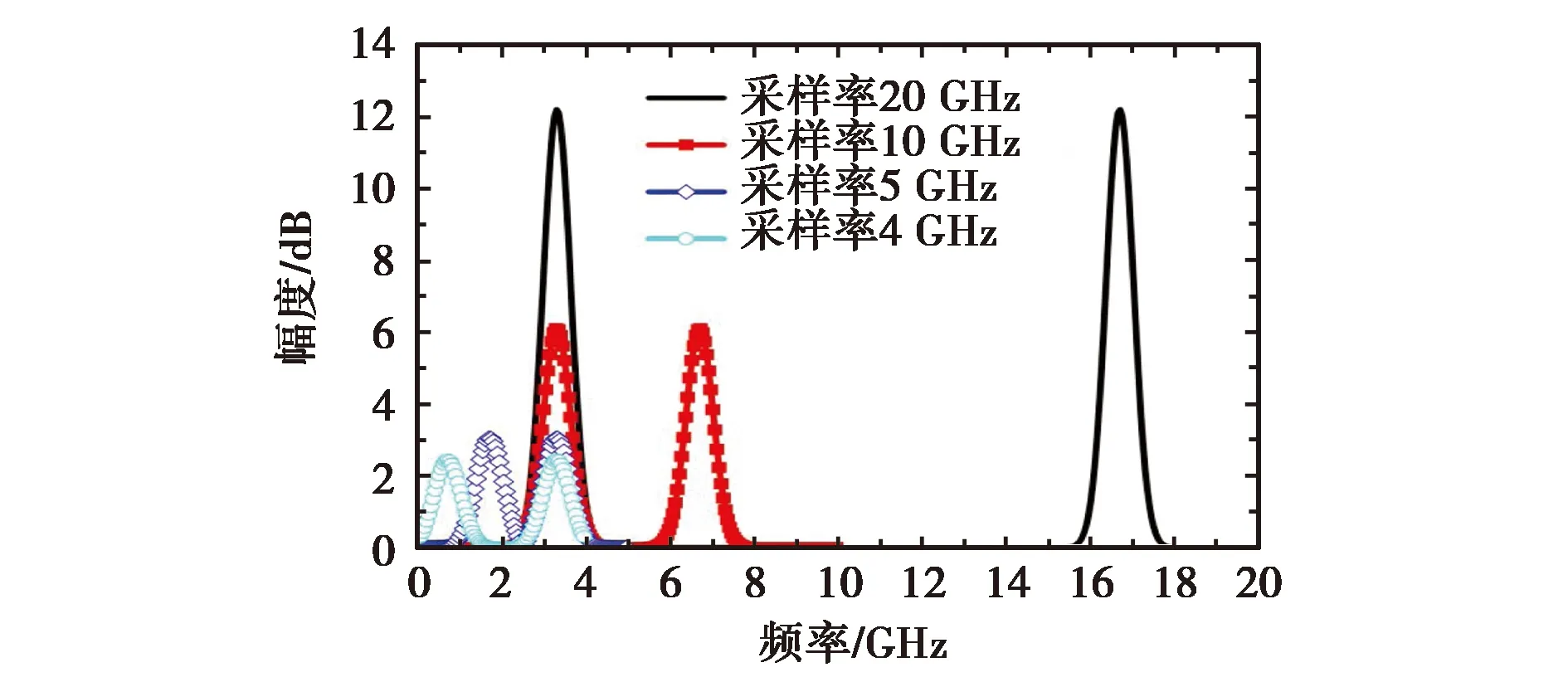
(a) 信号的频谱
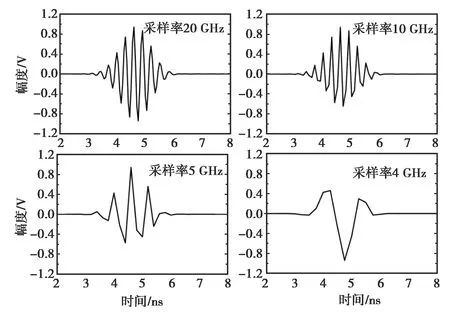
(b) 时域信号波形
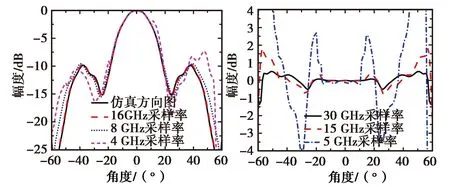
(c) 不同采样率3 GHz频点方向图实测结果图6 不同采样率采样结果
图6给出了第一类时间采样间隔误差对采样信号的影响.采样信号为图5中测试得到的采样信号,采样信号的频谱为2~5 GHz,实线为实测结果的频谱,时间采样间隔Δt=0.05 ns(采样率为20 GHz),实心方块线为Δt=0.1 ns(采样率为10 GHz)时采样信号的频谱,空心菱形线为Δt=0.2 ns(采样率为5 GHz)时采样信号的频谱,空心圆形线为Δt=0.25 ns(采样率为4 GHz)时采样信号的频谱.从图6(a)的频谱对比可以看到:在不满足奈奎斯特采样定律时信号的频谱会发生混叠,这样的采样信号在进行最后远场区方向图计算时会严重影响结果的准确性.而在满足奈奎斯特采样定律时,采样信号的采样率越高,信号频谱的幅值越高,这样信号的分辨率会越高.从图6(b)可以看出,在采样率为10 GHz(最大频率的2倍,满足奈奎斯特采样定律的最小采样率)时信号波形基本没有发生变化,只是幅值有所变化,而在采样率继续降低后,信号的波形发生了变化,这样会丢失很多信息,也对应了图6(a)中频谱混迭丢失频域信息的现象.
图6(c)给出了根据不同采样率采集到的信号计算得到的3 GHz频点的E面方向图. 可以看出在采样率为5 GHz时,信号从主瓣开始就出现了明显的偏差,在采样率为10 GHz时副瓣电平的误差大概为0.7 dB,在采样率为20 GHz时副瓣电平的误差在0.3 dB以下.所有计算结果都包含了探头位置误差等误差,计算结果已经针对信号源稳定度误差进行了修正.5 GHz采样率的计算结果出现比较大误差的原因是因为信号的频谱出现了混迭,信号的频域不是真实的频谱,信号频谱幅值较低,导致接收信号的信噪比很低,从而导致了结果出现明显的误差.10 GHz采样率的计算结果与20 GHz采样率的计算结果相比误差较大,在实际测试中不能被接受,导致10 GHz采样率计算结果的误差的主要原因是接收机为数字采样示波器,在进行采样时示波器的采样率并不能完全保证精确达到要求的采样率,所以采样率在满足奈奎斯特采样定律的下限时,有可能实测信号中的采样点没有满足采样率,从而导致计算结果出现误差.
当测试过程中的时域采样间隔Δt发生漂移时,也会导致最终的测试结果存在误差.这个漂移误差就是第二类时间采样间隔误差项.采样示波器在进行采样时,信号采样间隔为固定值,但是实际采样间隔有一定误差,这样会导致采样信号产生误差,进而影响最后的测试结果.这类误差对测试结果的影响体现在对信号进行频域计算时,需要对时域信号进行离散傅里叶变换(Discrete Fourier Transform,DFT),采样点间隔和对应采样数值决定了频域信号的幅值相位,采样示波器的采样点间隔误差会导致采样信号幅值相位的错误,进而导致频域结果的误差.由于信号的频域信息是通过傅里叶变换得到的,时间点对应频域上的频点,时间采样间隔误差在频域上会造成在对应频点处的频谱信息的误差,影响时域信号的频域信息.第二类误差属于系统的随机误差,可以参照类似频域误差项进行测试得到误差导致的不确定度,在采样示波器灵敏度很高时甚至可以忽略不计.
在实际测试中,对时间采样间隔即信号采样率的选取并非越高越好,上面的计算是在没有噪声等干扰信号的情况下得到的,在实际测试中,当信号长度一定时,采样率越高,采样信号中的噪声对正确的采样信号的影响会越严重,同时第二类时间采样间隔误差对信号的影响也会越明显,因此时间采样间隔的选择需要综合考虑仪器的性能以及采样信号的时间长度.
2.4 采样时间长度误差
时域近场测试最后的一项误差就是采样时间长度误差.因为时域测试的信号是一个连续信号,不同于频域的点频采样,时域采样信号需要完整地将信号采集,就需要一定的信号采集时间,采集时间过长,会将下一个周期的采样信号采集进来,而采集时间过短则会无法采集到完整信号波形.所以采样时间长度误差的实质是采样时间长度的上限和下限对采样信号造成的影响.
采样时间长度的上限就是前面所说的采集到下一周期信号的第一个信号点,在这个长度之内的采样信号时间长度理论上来说都是可以的.但是在实际测试中待测天线的辐射信号长度是一定的,采样时间长度越长,采集的信号的数据越大,会影响计算效率,采样的结果也会包含越多的系统噪声,在计算远场区方向图时会影响计算结果的准确性,所以需要根据采样信号的信噪比来选择时间的最长采样长度.采样时间长度的下限就是从开始采样到将待测天线的辐射信号完全采样完毕的时间,如果采样时间长度过短,会导致采样信号失真,对最终结果的准确性造成影响.
图7模拟了采样到两个周期信号时间采样长度上限和下限长度的选取,三条线分别表示信号的三个时间截断点,截断点后的信号不再采样,最左侧折线表示时间采样长度的下限值,即本周期内截断时间点后的信号为零;最右侧点状线表示采样时间长度的上限值,即采样进入下一周期,信号不再为零;中间点折线代表的是考虑实际测试中噪声存在情况下采样长度,处于采样时间长度上下限之间.
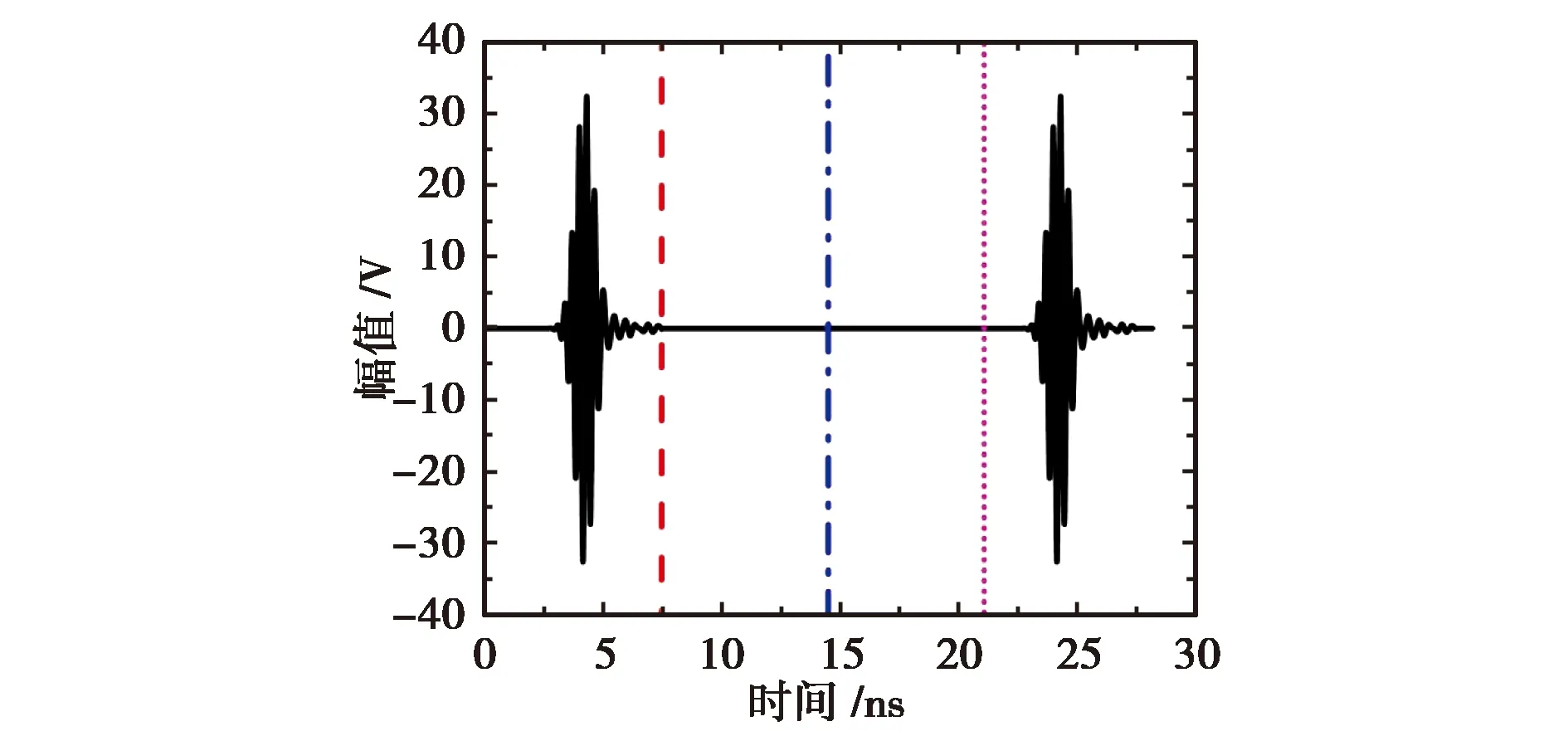
图7 不同采样长度示意图
在时域测试中用来控制采样时间长度的方法一般是采用“时间门”技术,即对采样进行时间上的截断,只保留截断时间内的信号,其他时间点上的信号不再进行计算.在实际测试中出于数据处理方面的考虑,将时间截断内的信号进行保留,时间截断外的信号置零,这样采样信号的长度统一同时去掉了大量的系统噪声.通过合理地对信号进行时间上的截断,可以有效地降低反射信号和系统噪声对测试的影响,但是将信号进行截断也会对信号造成一定影响,导致信号频谱的缺失,进而影响测试的精度.
下面给出利用不同长度的时间门对同一个接收信号进行截断,将截断后的信号在频域进行分析,给出时间采样长度误差对测试的影响.为了避免实际测试中噪声对测试结果的影响,只单纯考虑不合理的时间截断对采样信号造成的影响,这里采用软件仿真的形式模拟对S波段标准喇叭在近场进行采样.激励信号采用图2(a)中高斯调制源.
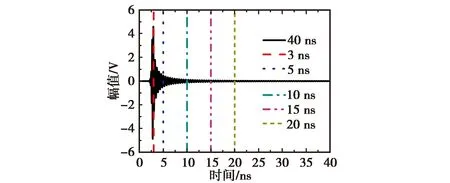
如图8(a)所示,采样信号是一个持续40 ns的信号,分别利用长度为3 ns、5 ns(去除天线与探头之间多重反射))、10 ns(信号幅值趋于稳定)、15 ns(信号幅值稳定)、20 ns(信号幅值极小可以近似忽略不计)的时间门进行截断,时间门外的信号全部填充为0.图8(b)给出了不同采样时间长度对信号进行截断后计算得到的在3 GHz频点的E面远场区方向图,图8(c)为所有方向图与仿真方向图差值的局部放大图.
由图8(b)可以看到:采样长度为3 ns的信号计算得到的远场区方向图的副瓣明显与仿真结果不符,最大差值达到了2.8 dBm,采样长度为5 ns和10 ns的信号计算得到的远场区方向图与仿真结果较为拟合,副瓣差值最大为1.5 dBm,而采样长度为20 ns和40 ns的信号对应的方向图副瓣差值最大值为0.4 dBm.由上面的仿真计算结果可以看到,如果采样时间过短会导致计算结果产生严重的误差,而采样时间长度应该为截断点外的采样信号基本为零或者可忽略不计时的信号长度.
图9给出了实际测试中利用不同时间采样长度得到的计算结果.图9(a)给出了时间门长度分别为40 ns(去除多重反射)、45 ns(基本完整信号)、95 ns(全部信号)的信号截取示意图.图9(b)给出了截断后信号计算得到的3 GHz的E面方向图的对比结果,图9(c)给出了所有方向图与仿真方向图差值的局部放大图.
(a) 不同时间长度截取信号示意图
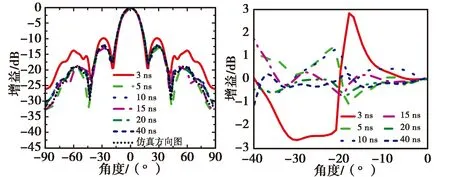
(b) 远场方向图 (c) 方向图差值局部放大图图8 时间采样长度计算结果
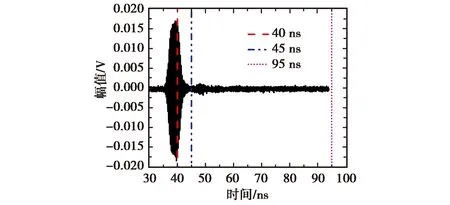
(a) 不同时间长度截取信号示意图
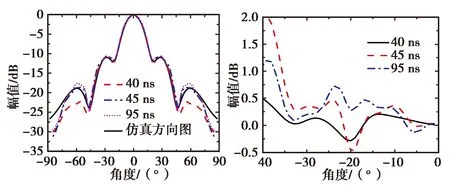
(b) 远场方向图 (c) 差值局部放大图图9 时间采样长度实测计算结果
由图9(b)可以看到,采样长度为45 ns的信号计算得到的结果与仿真方向图的结果比较吻合,副瓣电平误差在0.4 dB左右,而采样时间过短(40 ns)或过长(95 ns)的计算结果与仿真结果的误差都要大于45 ns长度的信号计算结果,误差分别在1.2 dB和0.9 dB左右.这是因为采样时间过短,信号信息丢失,与仿真结果一致;采样时间过长会因为过多噪声进入数据计算过程,导致计算出现较大误差,因此在实际测试中时间采样长度应尽量选取完整信号长度,避免因为信号采样长度过短或者过长导致结果出现较大的误差.
3 结 论
本文通过参考频域近场测试中误差项的分类及分析过程,给出了时域近场测试技术在具有频域测试技术的误差项外,还具有的四个独有误差项:探头调制误差、信号源稳定度误差、时间采样间隔误差、时间采样长度误差.在给出这四项独有误差项后,分别在机理上给出了误差产生的原因及误差对测试结果造成的影响,并通过仿真和实测的方式给出了在理想情况下的结果和包含误差项时的结果的对比.下一步工作是在明确误差项后对各个误差项进行定量分析并进行误差修正,给出误差不确定度分析.
[1] YAGHJIAN D. Upper-bound errors in far-field antenna parameters determined from planar near-field measurements, part 1: analysis[S]. Washington D. C.: Natational Bureau Stand, Tech Note 667, 1975.
[2] NEWELL A C. Error analysis techniques for planar near-field measurements[J]. IEEE transactions on antennas and propagation, 1988, 36(6): 754-768.
[3] IEEE Recommended practice for near-field antenna measurements[S/OL]. IEEE 1720-2012, 2012.[2017-01-10]. IEEE Recommended practice for near-field antenna measurements
[4] BUCCI O M, MIGLIORE M D. A new method for avoiding the truncation error in near-field antennas measurements[J]. IEEE transactions on antennas and propagation, 2006, 54(10): 2940-2952.
[5] KIM K T. Truncation-error reduction in 2D cylindrical/spherical near-field scanning[J]. IEEE transactions on antennas and propagation, 2010, 58 (6): 2153-2158.
[6] CANO-FACILA F J, PIVNENKO S, SIERRA-CASTANER M. Reduction of truncation errors in planar, cylindrical, and partial spherical near-field antenna measurements[J]. International journal of antennas and propagation, 2012, 42(6): 1-19.
[7] HANSEN T B, YAGHJIAN A D. Planar near-field scanning in the time domain 1:formulation[J]. IEEE transactions on antennas and propagation, 1994, 42(9): 1280-1291.
[8] HANSEN T B, YAGHJIAN A D. Planar near-field scanning in the time-domain part 2: sampling theorems and computation schemes[J]. IEEE transactions on antennas and propagation, 1994, 42(9): 1292-1300.
[9] HANSEN T B, YAGHJIAN A D. Formulation of probe-corrected planar near-field scanning in the time domain[J]. IEEE transactions on antennas and propagation, 1995, 43(6): 569-584.
[10]刘超, 薛正辉, 高本庆, 等. 时域近场测量采样平面选择分析[J]. 电波科学学报, 2001, 15(4): 512-516.
LIU C, XUE Z H, GAO B Q, et al. The analysis and selection of sampling plane in time-domain near-field measurement[J]. Chinese journal of radio science, 2001, 15(4): 512-516. (in Chinese)
[11]WANG N, XUE Z H, YANG S M, et al. Antenna time domain planar near field measurement system[J]. International journal on wireless and optical communications, 2006, 3(2): 1-7.
[12]薛正辉, 楼世平, 杨仕明, 等.“时间窗”对天线时域平面近场测试结果的影响[J]. 电波科学学报, 2007 22(1): 158-165.
XUE Z H, LOU S P, YANG S M, et al. Effect of time-gate on antenna planar near-field measurement in time domain[J]. Chinese journal of radio science, 2007, 22(1): 158-165. (in Chinese)
[13]GUY A E,VANDENBOSCH. Radiators in time domain-part I: electric, magnetic, and radiated energies[J]. IEEE transactions on antennas and propagation, 2013, 61(8): 3995-4003.
[14]吴洋, 薛正辉, 任武, 等. 时域平面近场散射测量研究[J]. 电波科学学报, 2015, 30(2): 351-356.
WU Y, XUE Z H, REN W, et al. Time domain planar near field scattering measurement[J]. Chinese journal of radio science, 2015, 30(2): 351-356. (in Chinese)
[15]闫润卿, 李英惠. 微波技术基础[M]. 3版. 北京: 北京理工大学出版社, 2004: 63-77.
曹猛 (1986—),男(蒙古族),内蒙古人,北京理工大学电磁场微波技术专业在读博士,主要从事天线近场测试方向研究.
薛正辉 (1970—),男,北京人,北京理工大学信息与电子学院副教授,主要从事阵列天线及天线近场测试方向研究.
任武 (1976—),男,山西人,北京理工大学信息与电子学院副教授,主要从事近场测试和电磁计算方向研究.
Error analysis on time domain planar near-field antenna measurement
CAO Meng XUE Zhenghui REN Wu LI Weiming ZHU Ruoqing CAI Hongwei
(BeijingInstituteofTechnology,Beijing100081,China)
Due to less researches on the error terms, the uncertainty analysis of the test results in time domain near-field antenna measurement remains uncompleted. To solve this problem, this paper presents four error terms which are ignored or inexistent in frequency domain near-field antenna measurement: probe modulation error, source stability error, time sampling interval error and time sampling length error, and the mechanisms of these errors are discussed. Finally, influence of the errors on the experimental results is present by simulation and test after the error terms are given.
time domain; near field measurement; error analysis;uncertainty analysis
2017-01-10
国家自然科学基金(No.61971003)
10.13443/j.cjors.2017011002
TN82
A
1005-0388(2017)01-0112-09
联系人: 薛正辉 E-mail:zhxue@bit.edu.cn
曹猛,薛正辉,任武,等. 天线时域平面近场测试的误差分析[J]. 电波科学学报,2017,32(1):112-120.
CAO M,XUE Z H,REN W,et al. Error analysis on time domain planar near-field antenna measurement[J]. Chinese journal of radio science,2017,32(1):112-120. (in Chinese). DOI: 10.13443/j.cjors.2017011002

