基于CVaR理论的综合能源系统经济优化调度

胡 浩 ，王英瑞 ，曾 博 ，张建华 ，史佳琪

（1.华北电力大学 新能源电力系统国家重点实验室，北京 102206；2.中国能源建设集团 天津电力设计院有限公司，天津 300400）

0 引言

随着社会经济的不断发展、能源和环境问题的日益突出［1］，在满足人们对多种能源需求的前提下，如何提高能源利用效率、实现产能清洁化成为当前各国关注的热点问题［2］。通过将电／气／热3种能源进行合理的规划和运行而形成的综合能源系统［3-6］IES（Integrated Energy System）为实现人类能源社会重要变革提供了一条重要的解决途径［7］。在IES中，微燃机、燃料电池 FC（Fuel Cell）、燃气锅炉 GB（Gas Boiler）等多种常规供能设备以及光伏电池和风机等清洁供能设备将电、气、热三者供能网络紧密地耦合起来，成为能源供给侧和用户负荷的能源转换平台。目前，在越来越多的可再生能源供电和供热设备接入的情况下，IES的供能侧和负荷侧都存在很强的不确定性，为消除不确定性的影响，在满足负荷需求的情况下尽量多地消纳可再生能源，IES中的可控供能设备的运行策略将发生很大变化。因此计及IES中存在的不确定因素开展的经济优化调度问题，具有重要的实际意义。

为此，越来越多的学者在此问题上展开了研究。文献［8］将IES供能侧和负荷侧之间的设备看作是一个energy hub，计及负荷需求的不确定性提出了一种energy hub能量管理的鲁棒优化方法；文献［9］采用确定性规划方法、二阶段规划方法和多阶段规划方法对考虑风电不确定性情况下的英国电-气IES的运行策略进行了研究；文献［10］基于燃气发电机组的快速调节特性研究了电-气IES中的风电消纳问题，建立了基于随机规划的调度模型；文献［11］考虑风电不确定性和需求侧响应，采用区间优化的方法研究了IES的调度问题；文献［12］研究了考虑不确定性存在的情况下计及运行安全约束的IES中电力和天然气系统的联合规划问题。以上文献在研究IES的优化调度问题时，无论是否考虑供能侧和负荷侧的不确定性，其目的均是通过恰当的方法建立调度模型并求解得到一种确定的设备调度策略和总的运行成本或其期望值，但对于不确定性给IES带来的运行成本增加的潜在风险并没有深入探讨，无法分析不确定性所造成的调度风险的严重程度。

鉴于以上问题，本文将用于风险评估的CVaR理论引入电／气／热IES中，研究了考虑供能侧和负荷侧中不确定性的经济优化调度问题。首先介绍了各种供能设备，利用概率统计方法描述了双侧不确定性量，然后建立了基于条件风险价值CVaR（Conditional Value at Risk）的IES经济调度模型，并将其转化为双层优化问题，采用快速粒子群优化算法和内点法对模型进行求解。通过算例仿真分析了CVaR理论中置信水平、多能流约束和设备调整费用对IES运行费用的影响。

1 IES中常见的供能设备

1.1 供电设备数学模型

a.微燃机CHP数学模型。

本文所研究的IES中采用目前实际工程中广泛采用的 Capstone C65 微燃机 CHP［13］，其额定功率为65 kW，额定转速为 96000 r／min，发电效率 ηMT可近似用式（1）表示。其中，PCHP为微燃机的电功率（kW），当PCHP变化不大时，也可将ηMT视为定值。

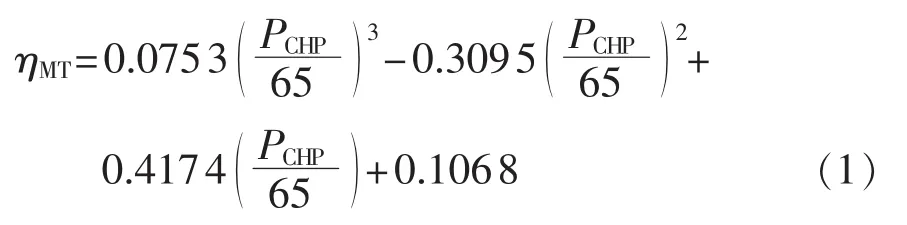
以天然气为一次能源的微燃机CHP机组单位时间内消耗的天然气量可表示为：

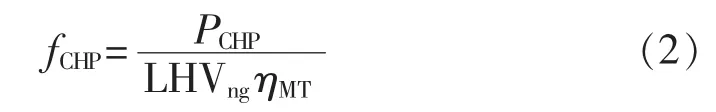
其中，LHVng为天然气热值，取 9.7 kW·h ／m3。

CHP单位时间燃料成本CCHP的表达式如下：

其中，Cng为天然气价格（元 ／m3）。

CHP的制热功率可表示为：

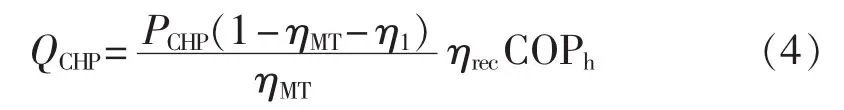
其中，η1为热损失率；ηrec为余热回收效率；COPh为溴冷机的制热系数。

b.燃料电池数学模型。

以天然气作为一次能源的燃料电池工作时单位时间消耗的天然气量如下：

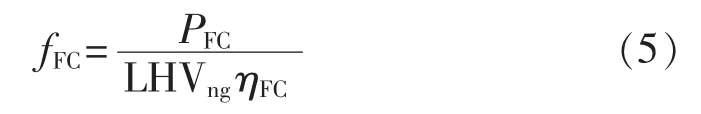
其中，PFC为燃料电池的发电功率；ηFC为发电效率，其取值与PFC有关，某型燃料电池的发电效率表达式如式（6）所示。

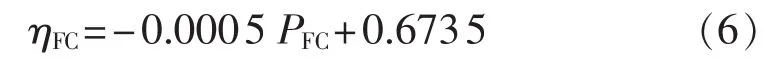
燃料电池单位时间的燃料成本CFC如下式所示：

c.光伏发电数学模型。

已知温度和光照强度后，光伏电池的输出功率可用式（8）表示。

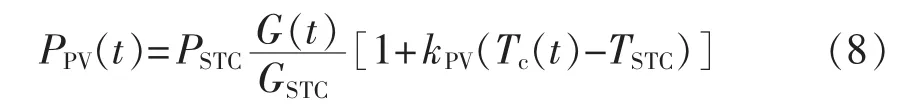
其中，PPV（t）为光伏电池的输出功率；GSTC、TSTC和 PSTC分别为标准测试条件（1000 W／m2、25℃）下的光照强度、光伏电池温度和最大输出功率；G（t）为t时刻光照强度（W／m2）；Tc（t）为光伏电池温度；kPV为功率温度系数，一般取-0.47。

d.风力发电数学模型。

风机输出功率和风速之间的关系可近似用式（9）表示。

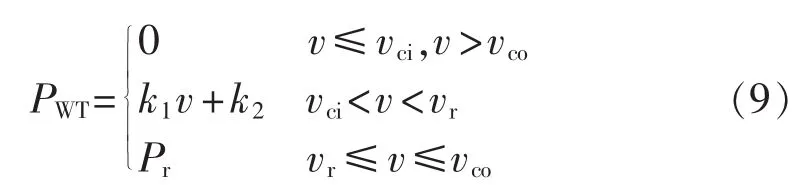
其中，PWT为风机的实际输出功率；Pr为额定功率；k1、k2为拟合参数；vci为切入风速；vr为额定风速；vco为切出风速。

1.2 供热设备数学模型

a.地源热泵数学模型。

本文采用地源热泵［14］GSHP（Ground Source Heat Pump）的简化数学模型，即用二次函数近似模拟输入和输出的关系，如式（10）所示。

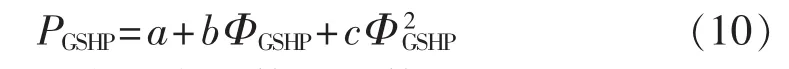
其中，a、b和c为二次函数的系数。

b.燃气锅炉数学模型。

燃气锅炉单位时间消耗的天然气量fGB如式（11）所示。

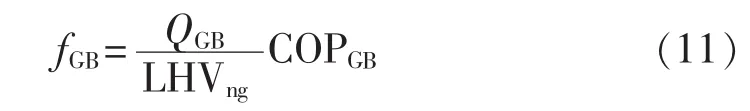
其中，QGB为燃气锅炉的制热功率；COPGB为制热系数。

燃气锅炉供热的单位时间燃料费用CGB为：

2 IES中不确定性数学描述

2.1 供能设备的不确定性

本文所研究的IES中供能侧存在不确定性的设备只有光伏电池和风机，常用描述风速不确定性的Weibull分布和描述光照不确定性的贝塔分布一般只用于描述风速和光照强度的长期平均分布情况，并没有计及相邻的不同时段之间的耦合情况，因此只适用于中长期的规划和运行调度问题。对于本文所研究的短期日前经济调度问题，为尽量接近实际情况，必须考虑风速和光照各自在一天中不同时段的时间耦合性，利用风速和光照的短期预测值来预测未来一天中风机和光伏的出力情况。为此，需对风速和光照的预测误差分布情况进行研究。

风速的预测误差Δv可以用风速预测值v¯偏离实际值v的大小程度来描述，即v=v¯+Δv。研究表明，风速的预测误差Δv可以看作是一个服从正态分布的随机变量［15］，其均值为 0，标准差为 σv，则风速实际值的概率：

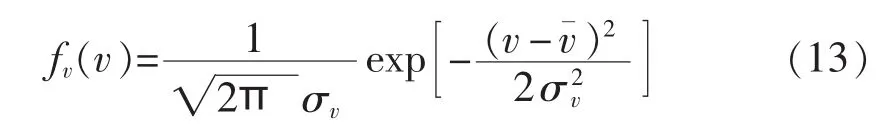
分布函数为：

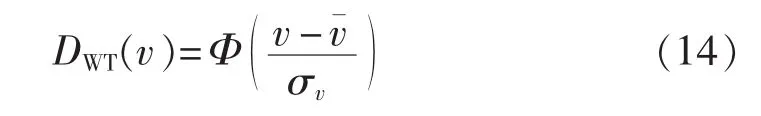
其中，Φ为标准正态分布函数。

根据式（9），风机的出力PWT与风速v不是线性关系，因此，即使风速v服从正态分布，PWT并不服从正态分布。利用式（9）和式（14）可以计算出风机的输出功率概率分布：

对于式（9）中的中间连续部分，由PWT=k1v+k2得 v=（PWT-k2）／k1，则该部分风机出力的概率密度函数为：

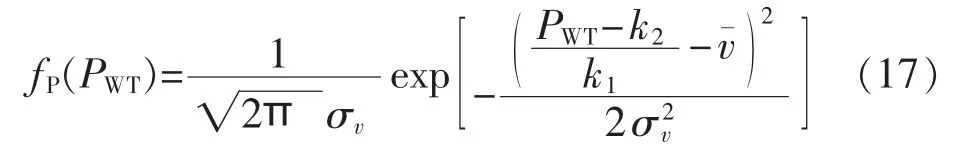
根据以上推导，在得到未来24 h的风机出力预测值，并经过统计得到标准差σv的情况下，便可对未来24 h的出力分布情况进行评估。

同样，根据文献［16］，对于光伏可以利用类似的方法处理。

2.2 电、热负荷的不确定性

电、热负荷作为IES经济调度的基本数据，在很大程度上决定了经济调度的结果。大量文献表明，对于不同时期的同一时间段，其电、热负荷水平大致呈正态分布。但由于实际中负荷存在最大值和最小值，因此，对于电、热负荷不确定性的描述宜采用有边界的正态分布模型［17-18］。

在实际预测中，预测值往往具有边界，因此需要对范围内的概率进行归一化处理［17］，设随机变量μ的最小、最大值分别为μmin和μmax，根据概率论中条件概率密度函数的概念，μ的概率密度函数可表示为：

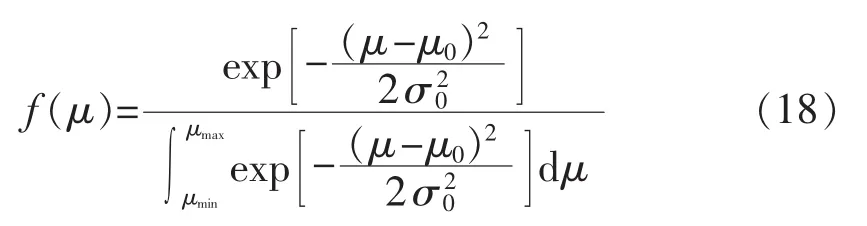
其中，μ0为随机变量μ的均值；σ0为μ的标准差。

设某时段电负荷预测值为P0，实际值为Pd，该时段内最小、最大负荷分别为 Pd，min和 Pd，max，Pd服从标准差为 σd1的正态分布，则在区间［Pd，min，Pd，max］内负荷实际值Pd的概率密度函数为：

同理，热负荷实际值Φd的概率密度函数fd（Φd）也可用类似方法得到，在此不再赘述。

2.3 不确定性场景生成及场景削减

本文采用拉丁超立方抽样方法对IES中上述含大量不确定量的场景进行随机抽样生成大量不确定性场景，进一步通过比较各个场景之间的概率距离对相似场景进行削减，具体步骤详见文献［17］。

3 基于CVaR的IES经济调度模型及求解方法

3.1 CVaR风险值的数学描述

CVaR是Rockafeller和Uryasev基于 VaR（Value at Risk）提出的一种改进风险分析方法［19-20］，有效地克服了VaR方法不能描述在不利情况发生时对损失程度的缺陷及其在次可加性上的不足。CVaR定义为在一定的投资周期内，当投资组合所承受的风险损失高于在给定置信水平下的VaR时的平均损失值。用数学公式可表示为：

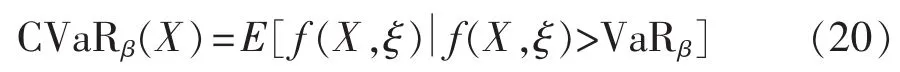
其中，f（X，ξ）为投资组合X的损失函数，ξ为可能影响损失函数的连续型随机变量；E［f（X，ξ）｜f（X，ξ）＞VaRβ］表示在 f（X，ξ）＞VaRβ的条件下f（X，ξ）的期望。

设随机变量ξ的概率密度函数为p（ξ），记损失函数 f（X，ξ）的分布函数为：

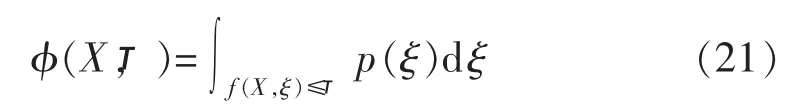
对于给定的置信水平β，投资组合X的VaR为：

则对应的CVaR表示为：

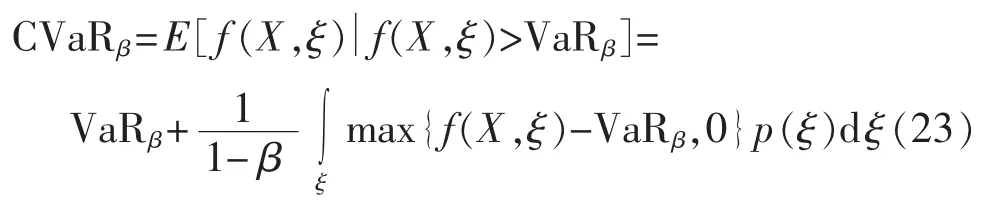
根据以上公式，只要已知概率密度函数p（ξ）就可以得到VaRβ，继而得到CVaRβ。

以上是对连续型CVaR的计算方法。实际中，在很多情况下计算CVaR时并不能满足连续性的条件，因此，需要对离散型的CVaR的计算方法进行推导。

采用各概率场景下的离散点来代替式（23）中的积分，则离散型CVaR的计算式如下：

其中，N为离散的总段数；Prn为第n段发生的概率。

利用上式对CVaR进行求解时需先计算同等置信水平下的VaR，给计算带来不便。根据文献［19］，构造以下优化问题：

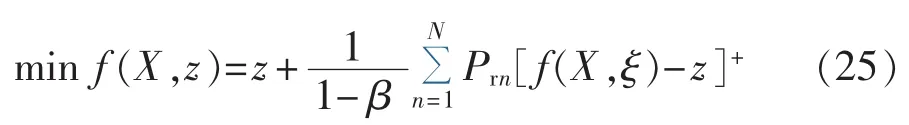
通过对以上问题进行求解，得到的目标函数f（X，z）的最小值即为 CVaRβ，对应的 z的取值即为VaRβ。

3.2 风险费用

不确定性对IES的影响主要是IES内的电功率、热功率、天然气流量的平衡，以及为保证功率、流量平衡所进行的各类供能设备的调整。为抵消以上不确定性的影响，IES的运行成本不仅包括从外部购买天然气和进行电能交换的成本，还包括为抵消以上不确定性对设备进行调整所产生的燃料费用、维护成本的变化以及由此附加的调整费用，该部分费用定义为IES经济调度的风险费用。

由于光伏、风机的出力预测值以及电、热负荷的功率预测值可能高于或低于实际值，由此产生的风险费用也应包含两部分：一部分为高估费用，另一部分为低估费用。

3.2.1 高估费用

当光伏、风机功率预测值高于实际值或电、热负荷预测值低于实际值时，需要可控设备增加出力或切除部分电、热负荷以达到功率平衡，由此产生的费用定义为高估费用。该部分费用包括调整可控设备所导致的燃料费用的变化、维护费用、调整费用和中断负荷的补偿费用，将其分为供电和供热的高估费用，描述方法如下。

a.供电高估费用。

供电高估费用表达式如式（26）所示。

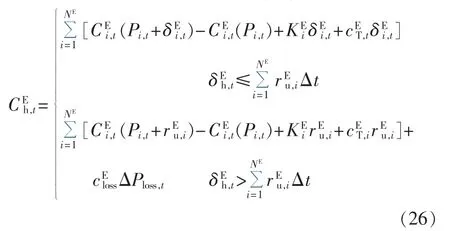
其中为由于不确定性的存在，可再生能源预测出力高于实际出力或负荷预测值低于实际值，系统为达到电功率平衡所需承担的风险费用为第i个发电设备在t时段的燃料成本函数，其表达式见1.1 节；Pi，t为对应的设备计划出力；NE为可控发电设备的数量为设备的调整功率为上爬坡速率；为设备的单位功率维护费用为设备的单位功率调整费用为 t时段的高估电量为中断单位电负荷的补偿费用为电负荷中断量；Δt为单位时间间隔。式（26）第二部分表示由于高估电量过高，各可控供电设备均按照最大上爬坡速率调整出力。

高估电量的表达式如下：

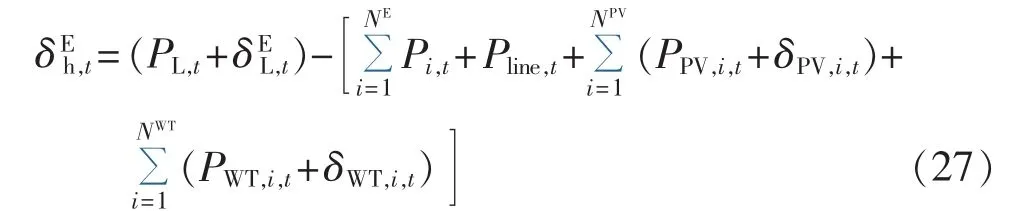
其中，PL，t为 t时段电负荷预测值；Pline，t为 IES 与外部电网交换的电功率；PPV，i，t和 PWT，i，t分别为光伏和风机的预测出力和 δWT，i，t分别为 t时段电负荷、光伏和风机的预测误差；NPV和NWT分别为光伏和风机的数量。

电负荷中断量表达式如下：

b.供热高估费用。

供热高估费用表达式如下：

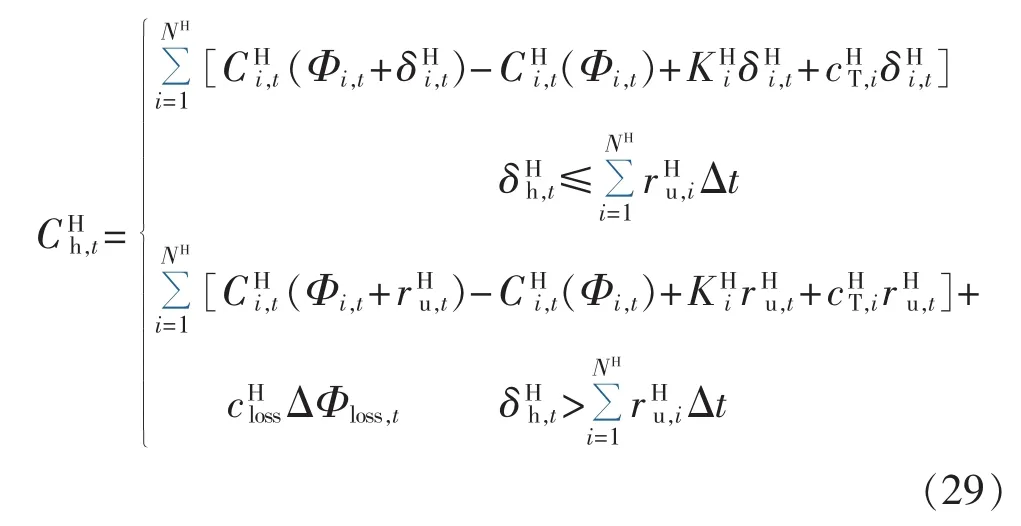
其中为由于热负荷功率预测值低于实际值，系统为达到热功率平衡所需承担的费用为第i个供热设备在t时段的燃料成本函数，其表达式见1.2节；Φi，t为对应的设备计划供热功率；NH为供热设备的数量为第i个供热设备在t时段的调整功率；为上爬坡速率为供热机组的单位功率维护费用为供热机组的单位功率调整费用为 t时段的高估热量为中断单位热负荷的补偿费用；为热负荷中断量。 式（29）第二部分表示由于高热电量过高，各可控供热设备的均按最大上爬坡速率调整出力。

高估热量表达式如下：

其中，ΦL，t为 t时段热负荷预测值；δHL，t为热负荷预测误差。

热负荷中断量表达式如下：

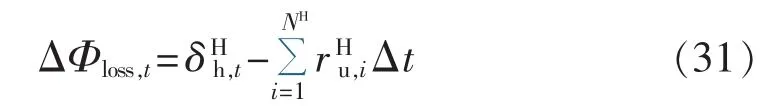
3.2.2 低估费用

当光伏、风机功率预测值低于实际值或电、热负荷预测值高于实际值时，需要可控设备降低出力或浪费部分可再生能源以达到功率平衡，由此产生的费用定义为低估费用。该部分费用包括调整可控设备所导致的燃料费用的变化、维护费用、调整费用和浪费可再生能源的惩罚费用，将其分为供电和供热的低估费用。

a.供电低估费用。

供电低估费用表达式如（32）所示。

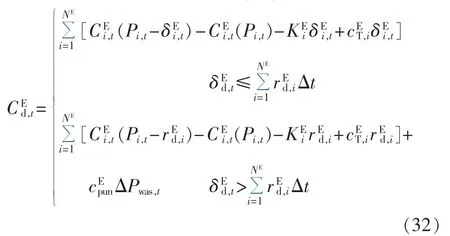
其中为由于不确定性的存在，可再生能源预测出力低于实际出力或负荷预测值高于实际值，系统为达到电功率平衡所需承担的风险费用为下爬坡速率为 t时段的低估电量为浪费单位电能的惩罚费用；ΔPwas，t为浪费电量。 式（32）第二部分表示由于低估电量过高，各可控供电设备均按最大下爬坡速率调整出力。

低估电量表达式如下：

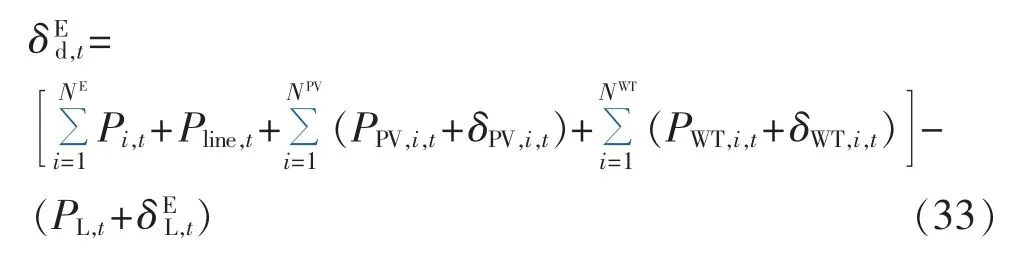
浪费电量表达式如下：

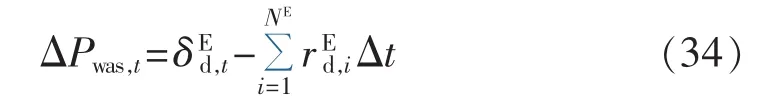
b.供热低估费用。

供热低估费用的表达式如下：

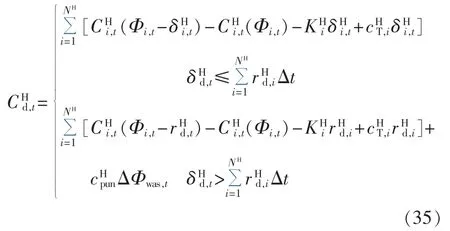
其中为由于热负荷功率预测值高于实际值，系统为达到热功率平衡所需承担的费用为供热机组下爬坡速率为 t时段的低估热量为浪费单位热能的惩罚费用；ΔΦwas，t为浪费热量。 式（35）第二部分表示由于低估热量过高，各可控供热设备均按最大下爬坡速率调整出力。

低估热量表达式为：

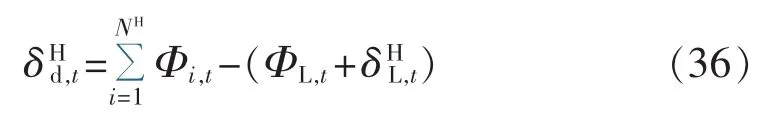
浪费热量为：

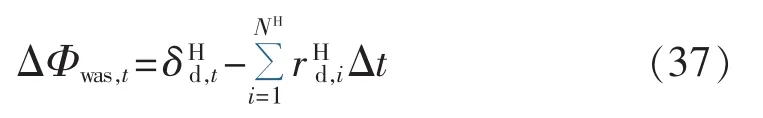
3.2.3 总风险费用

IES经济调度在t时段的总风险费用为以上高估费用和低估费用之和，如下所示：

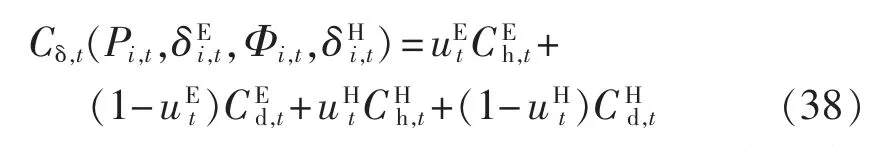
其中均为0-1变量，当时表示存在供电高估费用时表示存在供电低估费用，当1时表示存在供热高估费用时表示存在供热低估费用。

上式中的均为指示变量，在削减后生成的某一特定场景下的特定时段二者已经确定，并不作为模型的决策变量处理，故在求解过程中并不存在。综合以上各推导过程，计及调度风险费用的IES在第s个场景下整个调度时段T的总运行费用可表示为：

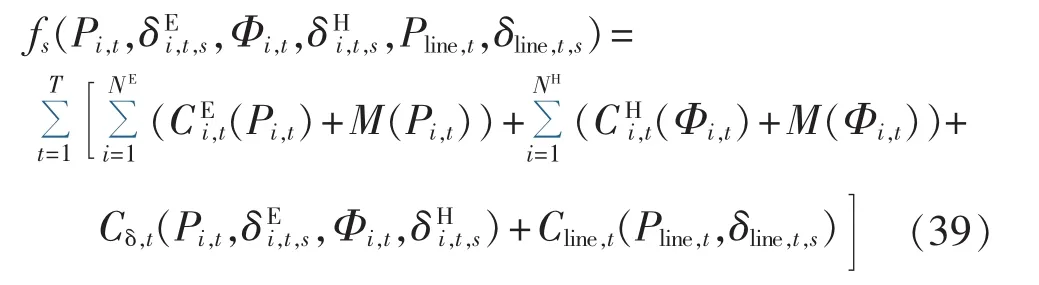
其中，Pi，t、Φi，t和 Pline，t等不带下标 s 的变量均表示可控供能设备的计划出力和 δline，t，s等带下标s的变量表示在不确定性发生后可控供能设备在第s个场景下的实际调整出力。式（39）等号右边第一、二项分别为IES内供电、供热设备在计划出力情形下的运行成本为对应的设备维护费用；第三项为第s个场景下的调度风险费用；第四项为IES与外部电网的电能交互费用。

3.3 IES经济调度的目标函数和约束条件

3.3.1 目标函数

本节选取IES总运行费用的CVaR为优化目标，建立基于CVaR的IES经济调度模型。根据3.1节中离散型CVaR的求解方法和3.2.3节中总运行费用的推导，可得目标函数的表达式如下：

其中，Ns为总场景数；Prs为第s个场景发生的概率。

3.3.2 约束条件

a.供能设备的计划出力和实际出力的上下限约束。

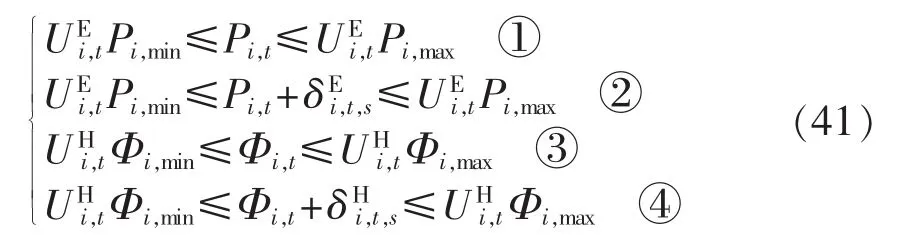
其中，Pi，min和 Pi，max分别为第 i台供电设备的出力下限和上限；Φi，min和 Φi，max分别第 i台供热设备的出力下限和上限分别表示供电和供热设备启停状态的0-1变量，等于1时表示启动，等于0时表示停机。

b.功率平衡约束。

在任意时段内，IES需满足电功率平衡、热功率平衡和天然气流量平衡约束：

其中，Δpt，s和 Δφt，s分别为 t时段电力网络和热力网络的功率损耗；fsource，t为t时段IES所需的天然气总量；Ne为以天然气为一次能源的供能设备数量；fi，t为t时段第i台设备消耗的天然气量为由于供能设备出力调整所造成的天然气消耗量的变化。

c.联络线功率约束。

IES和外部电网的联络线的交互功率需满足上下限约束：

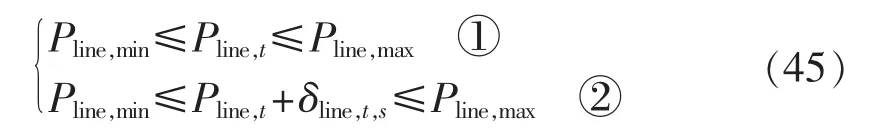
其中，Pline，max和 Pline，min分别为 IES 与外部电网的联络线的功率上、下限。

d.机组爬坡率约束。

供电和供热设备的出力变化需满足上爬坡率和下爬坡率约束：

e.多能流约束。

IES的电力子系统、热力子系统和天然气子系统中各线路、管道和节点上的状态量和控制量之间需满足多能流约束，具体约束详见文献［5］。

f.系统状态量约束。

为保证IES的安全稳定运行，电力子系统、热力子系统和天然气子系统中的状态量 x=［θ，U，m，Ts，load，Tr，load，Π］T（θ、U、m、Ts，load、Tr，load、Π 分别为电力子系统各节点电压相角、电压幅值，热力子系统各管道流量、负荷节点供热温度、负荷节点回热温度，天然气子系统压力降）需处于规定的范围内，用下式表示：

其中，xt，s为第 s 个场景下 t（t=1，2，…，T）时段的系统状态量向量；xmin和xmax分别为由各状态量的下限和上限组成的列向量。

3.4 模型求解

第3.3节中所建模型包含大量的优化变量，属于混合整数非线性规划（MINLP）问题，将其进行整体求解会带来计算量大、计算速度慢等问题。因此，需对优化变量和模型的关系进行分析，以确定合适的求解方法。首先，对于优化模型中存在的系统控制变量和状态变量，表示二者关系的是文献［5］中的多能流约束。对于该部分，可将状态变量作为依从变量，将控制变量作为决策变量，这样每次确定决策变量的值后，可应用基于Newton-Raphson算法［5］的多能流计算方法计算出对应的系统状态变量。利用这种方法可显著降低求解优化模型时算法处理等式约束的时间。其次，用X表示与不确定场景无关的变量，包括各设备的计划出力以及z，用Xs表示与不确定场景有关的变量，即各场景下可控供能设备的调整出力。将原优化模型表示成如式（48）所示的简化形式。

其中，e（X）为 X 函数；h（X）=0 和 g（X）≤0 分别表示3.3.2节中的约束条件中仅与设备计划出力有关的等式和不等式约束；hs（X，Xs）=0 和 gs（X，Xs）≤0 分别表示3.3.2节中的约束条件中与各场景下设备调整出力有关的等式和不等式约束。

简化形式的优化模型中，Xs的取值仅直接影响对应 fs（X，Xs），而 X 对各 fs（X，Xs）及 F（X，Xs）的其他部分均产生影响。 另外，分析可知［fs（X，Xs）-e（X）］+与 fs（X，Xs）正相关，而 Prs和 1／（1-β）均为正，故目标函数 F（X，Xs）与 fs（X，Xs）正相关。 因此，要使目标函数 F（X，Xs）取得最小值，各 fs（X，Xs）需在 X 确定的情况下调整Xs取得各自的最小值。

根据以上分析，对3.3节中的模型进行重新整理，得到如下的双层优化模型。

a.上层优化模型。

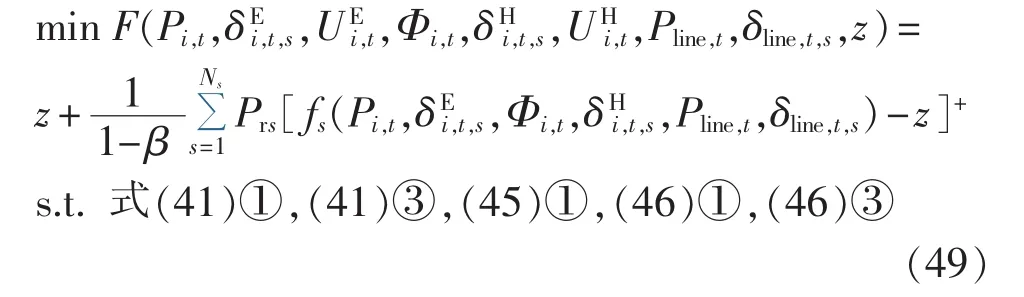
上层优化模型仍为MINLP问题，其中的多能流潮流采用扩展的Newton-Raphson算法［5］进行计算。

b.下层优化模型。

下层优化模型包含Ns个子问题，其中每个子问题均为仅包含连续变量的非线性规划问题，第s（s=1，2，…，Ns）个子问题的目标函数和约束条件如下：

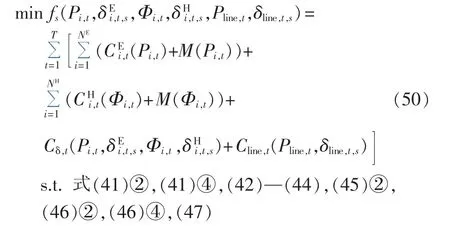
约束条件中，除上述各等式和不等式约束外，还包含文献［5］中的各等式约束。

针对以上基于CVaR的IES的经济调度问题的解法已有大量研究，其中比较有效的方法是智能优化算法与传统数学规划相结合的方法［13］，粒子群优化算法具有编码方式灵活和收敛速度快的特点，在求解包含大量等式和不等式约束的MINLP问题方面具有明显的优势，广泛应用于求解电力系统和IES的规划、调度问题；内点法作为一种基于梯度方向的经典数学规划方法，在求解目标函数和约束条件均可微的连续型非线性规划问题方面具有寻优速度快、数值稳定性高和精确性高的特点。因此，本文拟采用快速粒子群优化算法［13］求解上述双层优化问题的上层问题，用内点法（MATLAB中的fmincon函数实现）求解下层各子问题，通过上层和下层的不断迭代最终求出原问题的最优解。

需要注意的是，每个子问题中包含对T个时段的系统状态量的求解，为缩短计算时间，该部分不宜用内点法，可以采用基于Newton-Raphson法多能流计算方法。因此，在进行下层问题求解时，暂时不考虑多能流约束及式（47）中对系统状态量的约束，而将其放到上层问题中作为不等式约束，将多能流计算方法嵌套到快速粒子群优化算法中，求出各场景下每个时段的状态量后进行检验。

本文采用基于快速粒子群优化算法和内点法的模型求解流程如图1所示。

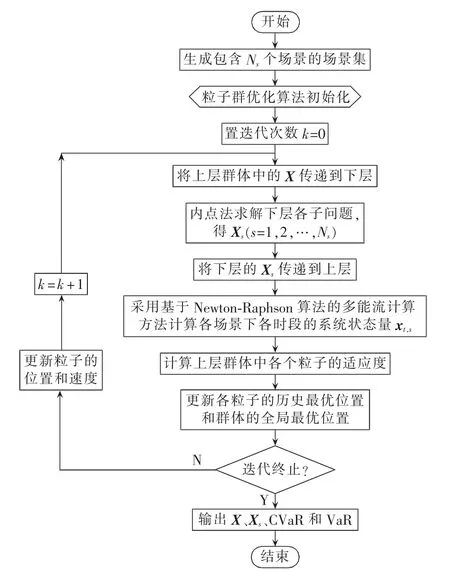
图1 基于快速粒子群优化算法和内点法的求解流程Fig.1 Flowchart of solver based on fast particle swarm optimization algorithm and interior point method

4 算例分析

4.1 基础数据

本文选取我国某地实际的IES为研究对象，其中包含微燃机、燃料电池、光伏电池、风机、地源热泵和燃气锅炉等供能单元。IES具体结构见图2，其中各供能单元具体参数详见表1，其中CHP工作于以电定热（FEL）模式。IES与外部电网进行电能交换的分时电价详见表2，天然气价格为2.51元／m3，各时段光伏、风机及总的电负荷、热负荷功率预测值详见图3、4，其中各电负荷节点功率因数均为0.9。假设光伏和风机的功率预测误差分别服从σ＝10%μ和σ＝15%μ的正态分布，电负荷和热负荷的功率预测误差服从σ＝5%μ的正态分布。

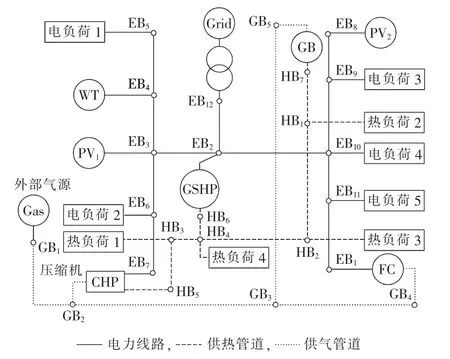
图2 IES算例结构图Fig.2 Structure of IES for case study

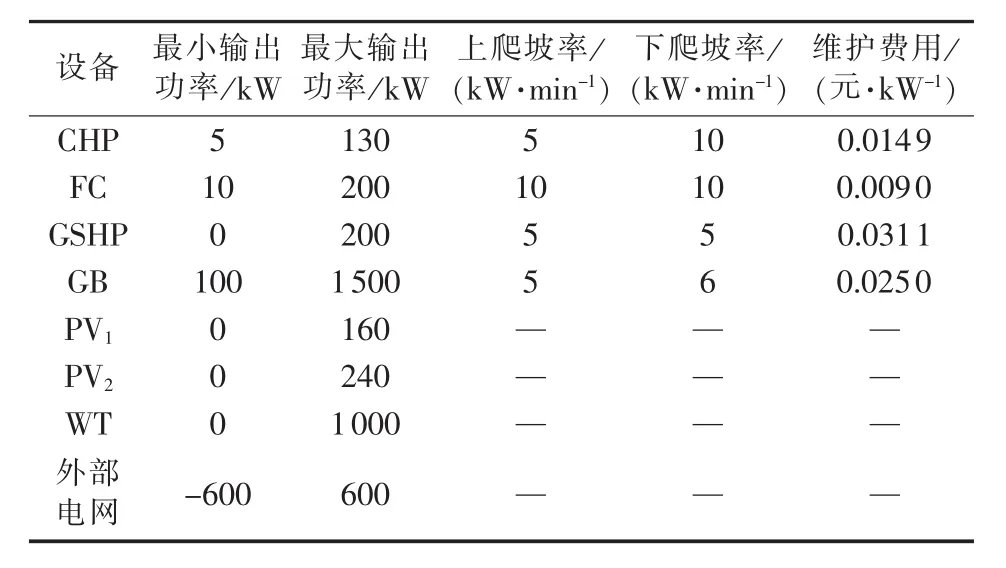
表1 IES各供能设备参数Table 1 Parameters of energy-supply devices in IES

表2 分时电价Table 2 Time-of-use tariffs

图3 PV和WT功率预测值Fig.3 Predicted PV power and WT power

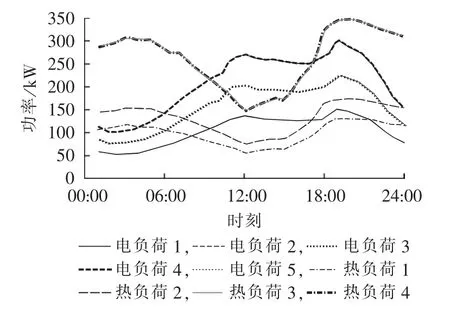
图4 电、热负荷功率预测值Fig.4 Predicted electric and thermal loads

设供电设备单位功率调整费用为0.52元／kW，供热设备的单位功率调整费用为0.42元／kW，中断单位电负荷以及热负荷的补偿费用分别为0.612元 ／（kW·h）和 0.452 元／（kW·h），浪费单位电能以及热能的惩罚费用分别为0.32元／（kW·h）和0.22元 ／（kW·h）。

本节利用3.3节提出的基于CVaR的IES经济调度模型在MATLAB中实现对IES算例的经济调度仿真分析，调度周期为T＝24，单位时间间隔为Δt＝1 h；经拉丁超立方抽样得到的初始不确定场景数为1000，经场景削减后得到的最终场景数Ns＝20；快速粒子群优化算法的迭代次数设为200；仿真所用的计算机CPU为Core i7-6700，主频3.4 GHz，内存容量为8GB。

4.2 结果分析

4.2.1 置信水平对仿真结果的影响

为研究置信水平β对仿真结果的影响，分别设置β＝0.80、0.85、0.90、0.95 和确定性条件（即 β＝0）下 5种仿真场景进行对比分析，利用3.4节中的基于快速粒子群优化算法和内点法的求解方法对3.3节中的经济调度模型进行求解，得到确定性条件下的日前运行费用9159.9元以及不同置信水平下的VaR和CVaR的值如图5所示，各置信水平及确定性场景下一天中不同供能设备的总出力情况如表3所示。

图5 不同置信水平下的VaR和CVaR对比结果Fig.5 Comparison of VaR and CVaR among different confidence levels

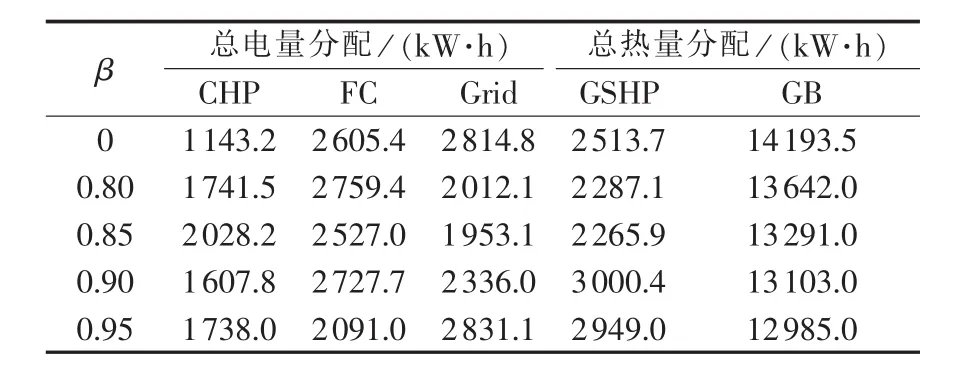
表3 不同置信水平下各供能设备的出力分配Table 3 Allocation of electric and thermal output powers among energy-supply devices for different confidence levels

通过对比确定性场景和各置信水平下的不确定场景可以看出，考虑不确定性下的IES经济调度运行费用普遍低于确定性下的运行费用，这一定程度上说明了在预测出力值存在误差的情况下，运用CVaR方法可有效降低运行的经济损失，减少资源浪费。

本节提出的优化模型在考虑可再生能源机组出力和电、热负荷不确定性的情况下，计及可控供能设备的调整费用寻找最优调度结果。由图5可知，随着置信水平β的增大，VaR和CVaR值都将增大，即系统所面临的调度风险增加；当β按相同的步长增大时，VaR和CVaR均增大，但增大的速度逐渐降低，且二者之差逐渐减小。这是由光伏、风机、电负荷及热负荷功率的不确定性预测误差呈正态分布所致，随着β的增大，系统所承受的潜在风险逐渐向正态分布的尾部移动，导致该部分所对应的运行费用期望值逐渐增大，但增速变缓。另外，由于在进行考虑潜在运行风险的经济调度时采用的供能设备的数学模型是非线性的，因此表3中各供能设备的总出力分配情况并不是线性变化的。

4.2.2 多能流约束对仿真结果的影响

本文提出的IES经济调度模型中包含了各子系统的支路和管道元件的特性约束，即多能流约束，因此能够分析调度过程中系统状态量的变化情况。在选定的Ns个场景中，不同置信水平下，电力、热力、天然气子系统各节点参数均在允许范围之内，分别取β＝0.90和0.95时计及多能流约束前后各节点参数最大最小值仿真结果加以分析，如图6—8所示。

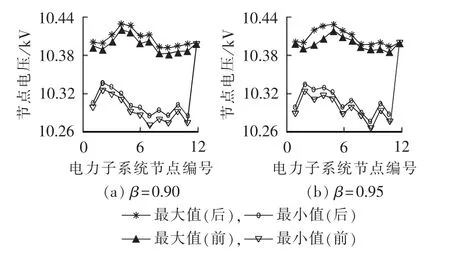
图6 电力子系统各节点电压最大、最小值Fig.6 Nodal maximum and minimum voltages of electric subsystem

图7 热力子系统各负荷节点供热温度最大、最小值Fig.7 Nodal maximum and minimum temperatures of thermal subsystem

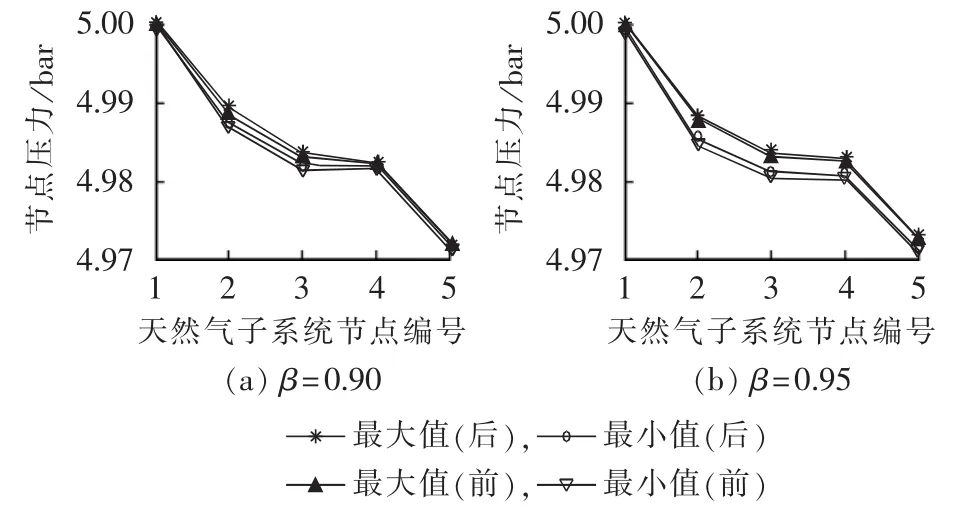
图8 天然气子系统各节点压力最大、最小值Fig.8 Nodal maximum and minimum pressures of gas subsystem

值得注意的是，本文在电力子系统中选取的并网点作为平衡节点，其电压为10.4 kV，因此虽然不计及多能流约束时电力子系统中系统变量并没有明显的越界行为，但从图中对比可知，在计及多能流约束时，电、热、气3个子系统具有很好的鲁棒性；在不计及多能流约束得到的调度结果应用于实际中时，随着并网点电压（热网平衡节点温度或气网平衡节点压力）的降低，整个IES的供能质量将会面临重大威胁。

由上图的仿真结果可知，对于本节所研究的IES，由于优化过程计及了多能流约束，在不同置信水平下，电力子系统的节点电压、热力子系统的节点温度和天然气子系统的节点压力等状态量均在允许的运行范围内。相对于通常所采用的不计及多能流约束的调度模型，本文所提出的基于CVaR并考虑多能流约束的经济调度模型可更好地保证IES的安全运行，避免为片面追求经济性而给系统安全运行带来影响，同时可为各节点控制量的调整提供一定的参考，这对于IES的运行具有重要意义。

4.2.3 设备调整费用对仿真结果的影响

为研究设备单位功率调整费用对仿真结果的影响，将3.2节中原定的供能设备的单位功率调整费用以cT0表示，在β=0.90的情况下将cT分别设为原调整费用cT0的25%、50%、75%、1.25倍和1.50倍，分别仿真得到运行费用期望值E、VaR和CVaR的值随cT的变化如表4所示。

表4 供能设备单位功率调整费用的仿真结果Table 4 Simulative results for different unit power adjustment costs of energy-supply device

由以上仿真结果可知，当cT变化时，总运行费用的期望值变化不大，但是随着cT的增大，VaR和CVaR逐渐减小，这是因为cT影响了总运行费用的分布情况。由于计入了设备调整所带来的运行费用的增加，当cT比较大时，总运行费用的分布更加集中，在同样的置信水平下CVaR和VaR都比较小，说明所建立的模型本身具有一定的鲁棒性，此时系统调度所承担的风险水平降低。以上仿真结果说明，采用基于CVaR的经济调度模型，可有效降低IES所承担的调度风险费用。

4.3 收敛性分析

为说明粒子群和内点法相结合算法在处理本文所提模型的收敛性，本文在图9中绘制了β=0.80、0.85、0.90和0.95的置信水平下的算法收敛曲线。从图中曲线可以看出4组仿真程序在经过200次迭代后都可有效收敛，并得到最优解。

图9 不同置信水平下目标函数的收敛曲线Fig.9 Convergence curves of objective function for different confidence levels

5 结论

本文研究了不确定性对IES优化调度产生的影响，建立了基于CVaR的IES经济调度模型，并转化为双层优化问题，运用快速粒子群算法和内点法进行求解，通过算例分析进行仿真。主要得到了以下结论。

a.CVaR方法能够很好地反映不确定量对IES调度问题的风险水平，从而有效地避免由于不确定因素所产生的经济损失；同时当置信水平提高时，系统所承受的调度风险也相应地增加，且电、热负荷在各供能设备之间的分配也发生变化。

b.调度模型中计及了电、热、气多能流的约束条件，由此得到的调度方案可保证系统的安全运行，更具有实际意义。

c.系统中可控供能设备的单位功率调整费用会影响到系统运行费用的分布，本文提出的基于CVaR的经济调度模型可有效降低IES所承担的调度风险，提高系统调度承担的风险水平。

参考文献：

［1］邓建玲.能源互联网的概念及发展模式［J］.电力自动化设备,2016，36（3）：1-5.DENG Jianling.Concept of energy internet and its development modes［J］.Electric Power Automation Equipment，2016，36（3）：1-5.

［2］吉平，周孝信，宋云亭，等.区域可再生能源规划模型述评与展望［J］. 电网技术，2013，37（8）：2071-2079.JI Ping，ZHOU Xiaoxin，SONG Yunting，et al.Review and prospect of regional renewable energy planning models［J］.Power System Technology，2013，37（8）：2071-2079.

［3］OMALLEY M，KROPOSKI B.Energy comes together：the integration of all systems［J］.IEEE Power& Energy Magazine，2013，11（5）：18-23.

［4］贾宏杰，王丹，徐宪东，等.区域综合能源系统若干问题研究［J］.电力系统自动化，2015，39（7）：198-207.JIA Hongjie，WANG Dan，XU Xiandong，et al.Research on some key problems related to integrated energy systems［J］.Automation of Electric Power Systems，2015，39（7）：198-207.

［5］王英瑞，曾博，郭经，等.电-热-气综合能源系统多能流计算方法［J］. 电网技术，2016，40（10）：2942-2950.WANG Yingrui，ZENG Bo，GUO Jing，et al.Multi-energy flow calculation method for integrated energy system containing electricity，heat and gas［J］.Power System Technology，2016，40（10）：2942-2950.

［6］于波，吴亮，卢欣，等.区域综合能源系统优化调度方法［J］.电力建设，2016，37（1）：70-76.YU Bo，WU Liang，LU Xin，et al.Optimal dispatching method of integrated community energy system［J］.Electric Power Construction，2016，37（1）：70-76.

［7］JIN H，HONG H，WANG B，et al.A new principle of synthetic cascade utilization of chemical energy and physical energy ［J］.Science China Technological Sciences，2005，48（2）：163-179.

［8］PARISIO A，VECCHIO C D，VACCARO A.A robust optimization approach to energy hub management［J］.International Journal of Electrical Power&Energy Systems，2012，42（1）：98-104.

［9］QADRDAN M，WU J，JENKINS N，et al.Operating strategies for a GB integrated gas and electricity network considering the uncertainty in wind power forecasts［J］.IEEE Transactions on Sustainable Energy，2014，5（1）：128-138.

［10］ALABDULWAHAB A，ABUSORRAH A，ZHANG X，et al.Coordination of interdependent natural gas and electricity infrastructures for firming the variability of wind energy in stochastic day-ahead scheduling［J］.IEEE Transactionson Sustainable Energy，2015，6（2）：606-615.

［11］BAI L，LI F，CUI H，et al.Interval optimization based operating strategy for gas-electricity integrated energy systems considering demand response and wind uncertainty［J］.Applied Energy，2016，167：270-279.

［12］ZHANG X，SHAHIDEHPOUR M，ALABDULWAHAB A S，et al.Security-constrained co-optimization planning of electricity and natural gas transportation infrastructures［J］.IEEE Transactions on Power Systems，2015，30（6）：2984-2993.

［13］李乐.微网的经济运行研究［D］.北京：华北电力大学，2011.LI Le.Study on economic operation of microgrid［D］.Beijing：North China Electric Power University，2011.

［14］SIVASAKTHIVEL T，MURUGESAN K，SAHOO P K.Optimization of ground heat exchanger parameters of ground source heat pump system for space heating applications［J］.Energy，2014，78：573-586.

［15］WANG J，SHAHIDEHPOUR M，LI Z.Security-constrained unit commitment with volatile wind power generation［J］.IEEE Transactions on Power Systems，2008，23（3）：1319-1327.

［16］NGUYEN D T，LE L B.Risk-constrained profit maximization for microgrid aggregators with demand response［J］.IEEE Transactions on Smart Grid，2015，6（1）：135-146.

［17］高亚静，李瑞环，梁海峰，等.考虑间歇性电源与负荷不确定性情况下基于多场景技术的主动配电系统两步优化调度［J］.中国电机工程学报，2015，35（7）：1657-1665.GAO Yajing，LI Ruihuan，LIANG Haifeng，et al.Two step optimal dispatch based on multiple scenarios technique considering uncertainties of intermittent distributed generations and loads in the active distribution system［J］.Proceedings of the CSEE，2015，35（7）：1657-1665.

［18］邓创，鞠立伟，刘俊勇，等.基于模糊CVaR理论的水火电系统随机调度多目标优化模型［J］. 电网技术，2016，40（5）：1447-1454.DENG Chuang，JU Liwei，LIU Junyong，et al.Stochastic scheduling multi-objective optimization model for hydro-thermal power systems based on fuzzy CVaR theory［J］.Power System Technology，2016，40（5）：1447-1454.

［19］URYASEV S.Conditional value-at-risk：optimization algorithms and applications［C］∥Computational Intelligence for Financial Engineering. ［S.l.］：IEEE，2000：49-57.

［20］ROCKAFELLAR R T，URYASEV S.Conditional value-at-risk for general loss distributions［J］.Journal of Banking&Finance，2002，26（7）：1443-1471.

［21］张锋，段余平，邱军，等.基于粒子群算法与内点算法的无功优化研究［J］. 电力系统保护与控制，2010，38（13）：11-16.ZHANG Feng，DUAN Yuping，QIU Jun，et al.Research on reactive power flow based on particle swarm optimization and interior point method［J］.Power System Protection&Control，2010，38（13）：11-16.

［22］余胜威.MATLAB优化算法案例分析与应用［M］.北京：清华大学出版社，2015：174-179.