计及P2H的电-热互联综合能源系统概率能量流分析

孙 娟，卫志农，孙国强，陈 胜，臧海祥，陈 霜

（河海大学 能源与电气学院，江苏 南京 211100）

0 引言

随着社会能源结构调整，节能减排压力不断增加，可持续的能源开发与利用模式被公认为未来能源行业发展和变革的方向。综合能源系统、能源互联网和“互联网+智慧能源”等概念的相继提出，打破了各能源系统分开规划、独立运行的既有模式，为能源系统的分析提供了全新视角，带动了多领域、多学科、多维度间的交融与革新［1-4］。综合能源系统一般涵盖集成的供电、供气、供暖、供冷、供氢和电气化交通等能源系统，以及相关的通信和信息基础设施［5］。其中，热电联供网络目前发展最为迅速［6］。

自20世纪开始，热网在全球范围内逐步建立［6］。随着热网的普及及热电联产CHP（Combined Heat and Power）机组的逐步应用，电力系统和热力系统耦合不断加深，电-热互联综合能源系统逐渐引起广泛关注。文献［7-8］建立了电-热互联综合能源系统稳态模型，并提出了一种有效的潮流计算方法。文献［6］研究了热电联合网络的状态估计。文献［9］提出了面向能源互联网的多能流静态安全分析的概念和方法。文献［10］重点分析了电热协调运行方式对风电消纳的促进作用。文献［11］研究了含燃料电池、风电、光伏的电-热微网最优协调调度。

近年来，以风、光为代表的分布式可再生能源发电出力的随机性和波动性严重制约了其发展［12］，如何增强其接入能力成为可再生能源系统构建的重点和难点。电转热P2H（Power-to-Heat）技术可将电网难以消纳的光伏出力转化为热能提供给热网，为分布式可再生光伏的消纳及电-热互联综合能源系统协同运行提供了新机遇。P2H元件包括热泵、电锅炉、储热机构等［13］。目前，以丹麦［14］和德国［15］为代表的欧洲各国，主要从P2H的技术可行性和经济性角度出发开展研究。文献［13］建立了基于P2H和需求侧响应的最优控制模型，用以评估其应用于城市地区风、光消纳的潜力。文献［16］提出了求解大规模多阶段优化问题的分解协调算法，分析了含P2H的电-热互联综合能源系统优化运行问题。然而，现有研究多数基于确定性的模型，未充分考虑分布式可再生能源的不确定性。

电-热互联综合能源系统的不确定性因素（例如分布式可再生能源出力波动、负荷波动、系统故障等）给系统的安全运行带来了极大的挑战。为此，本文建立了含光伏的电-热互联综合能源系统概率能量流模型，以定量评估不确定性因素对系统概率能量流的影响以及P2H对光伏消纳的积极作用。

本文首先建立热力系统稳态能量流模型，并通过CHP机组和P2H元件建立电力系统和热力系统的耦合关系；其次，对系统中光伏出力和电、热负荷等随机变量建模，并最终建立含光伏的电-热互联综合能源系统概率能量流模型；在此基础上，采用基于Nataf变换和拉丁超立方采样LHS（Latin Hypercube Sampling）的蒙特卡罗模拟法，即CLMCS（Correlation LHS-Monte Carlo Simulation）法［17-19］，定量评估 P2H对电力系统和热力系统概率能量流的影响，同时计及输入变量的随机性和相关性。对含光伏的巴厘岛电-热互联综合能源系统进行算例分析，结果验证了本文所建立模型的可行性与有效性。

1 电-热互联综合能源系统稳态能量流模型

电力系统和热力系统通过CHP机组和P2H元件耦合成电-热互联综合能源系统。电力系统与热力系统间的关系可以概括为：一方面两者有共同的源（CHP机组），另一方面热力系统也是电力系统的负荷（P2H 元件消耗电能）［9］。

1.1 热力系统稳态模型

热力系统主要由热源、热网和热用户3个部分组成，承担着热力系统生产、传输和交换的职能［10］。热网一般由输送和回收管道构成。管道中充以热水或热水蒸汽（目前，在我国最常用的是热水管网），将热量从热源侧输送到终端热用户侧［7］。

1.1.1 水力模型

热网管道流量通过水力模型确定。热网水力模型与电网模型存在很多相似之处，如表1所示。

表1 电网与热网基本定律类比Table 1 Analogy of basic rules between electrical and heat networks

热网水力模型基本定律具体表述为：

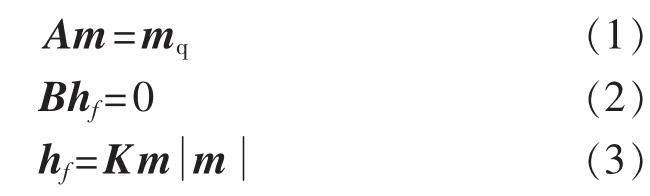
其中，A为热网节点-支路网络关联矩阵；m为热网管道流量；mq为注入节点的流量；B为热网回路-支路环路关联矩阵；hf为由管道摩擦造成的压头损失；K为管道的阻力系数，在很大程度上取决于管道的直径，并可由摩擦因数 f计算得到，详见文献［8］。

1.1.2 热力模型

热网节点温度通过热力模型确定。对于每一个热网节点，供热温度Ts表示热水注入节点之前的温度，输出温度To表示热水流出节点时的温度，回热温度Tr表示热水流出节点并与其他管道的热水混合汇入回收管道之后的温度。热力模型包括热量方程、管道温度降落方程和节点混合温度方程，即：

其中，Φ为负荷得到或热源提供的热量；Cp为水的比热容；Tstart和Tend分别为管道起点和终点的温度；Ta为环境温度；λ为管道单位长度传热系数；L为管道长度；m为某一条管道的流量；mout和min分别为流出和注入节点的流量；Tout和Tin分别为流出和注入节点的热水温度。

1.2 耦合元件模型

1.2.1 CHP机组模型

CHP机组利用天然气燃烧时的高品位热能做功驱动微燃机发电，所排出的高温余热烟气经溴冷机后用于取暖及供应生活热水［20］。CHP机组同时产热产电，可作为电力系统和热力系统两者共同的源。依据其热电比是否变化，可分为定热电比（如燃气轮机、往复式内燃机）和变热电比（如抽气式汽轮机）2种类型，如图1所示。

图1 CHP机组的热电关系Fig.1 Relation between heat generation and power generation of CHP units

其中和cm分别为定热电比CHP机组的电出力、热出力和定热电比和cz分别为变热电比CHP机组的电出力、热出力和变热电比；ηe为变热电比CHP机组的冷凝效率；Fin为燃料输入速率。cm为一恒定值，而cz为一个变化的值，但是在实际某个时段内，cz保持不变［9］。

1.2.2 P2H元件模型

P2H元件包含热泵、电锅炉、储热机构等［13］。热泵是一种利用高位能使热量从低位热源流向高位热源的节能装置。电锅炉直接把电能转换为热能。两者电热转换效率分别为：

其中，COP为热泵电热转换效率（Coefficient Of Performance）；Php和Φhp分别为热泵消耗的有功功率和相应的热出力；ηb为电锅炉电热转换效率；Pb和Φb分别为电锅炉消耗的有功功率和相应的热出力。

一般而言，热泵的COP可以达到3，而高效节能电锅炉的效率ηb最高只能达到98%。另一方面，热泵的投资建设费用相对较高，且其应用的局限性（如低位热源容量限制、地域限制等）极大地降低了电热转换的灵活性。而电锅炉安装简单、控制灵活且维修更换方便［20］。因此，热泵常与CHP机组联合使用来改善系统热出力，如图2所示。其中，γ为热泵消耗的有功功率占CHP机组电出力的百分数；Psource和Φsource分别为热泵与CHP机组联合系统的电、热出力。电锅炉则在电价引导下配合CHP系统满足热负荷需求并增加谷时段用电量，对电热负荷进行峰谷协调［20］。文献［21］从能源、经济和环境角度出发，对比分布式CHP中的电锅炉和热泵的应用潜力。

图2 热泵与CHP机组联合系统Fig.2 Integration of CHP unit and heat pump

1.3 电-热互联综合能源系统稳态能量流分析

电-热互联综合能源系统稳态能量流分析基于电力系统潮流方程和热力系统水力-热力方程式（1）—（6），并计入系统间能量的流动（式（7）—（10））。 本文采用最常用的牛顿-拉夫逊法求解，修正方程如下：

其中，P和Q分别为电力系统节点的有功和无功；ΔF为输入变量修正量；θ和U分别为电力系统节点电压的相角和幅值；ΔX为状态变量修正量；J为雅可比矩阵，由电力子阵Je、电热子阵 Jeh、热电子阵Jhe、热力子阵 Jh组成。

基于式（11）、（12）同时求解电力系统潮流、热力系统水力-热力潮流。其中，网络关联矩阵A和环路关联矩阵B根据管道流量m的方向每次迭代更新。

2 随机变量概率模型

电-热互联综合能源系统的不确定性因素来源于电力系统、热力系统以及耦合机构中的不确定量。本文主要研究系统注入量（如光伏出力、负荷等的输出功率）的不确定性，暂不考虑参数的不确定性。

2.1 光伏出力的概率特性

光伏出力具有强随机性和波动性的特点。研究表明，光照强度在短时间尺度（几个小时或者一天）或者长时间尺度内，都服从Beta分布［22］。光伏出力也满足 Beta［23］分布，概率密度函数为：

其中，α和β为Beta分布的形状参数；Pa和Pmax分别为光伏电站实际有功出力和最大有功出力。

光伏发电机组采用恒功率因数控制。假设光伏发电机组的功率因数为1，则其无功出力为0。

2.2 电、热负荷的概率特性

一般而言，正态分布可以较好地描述电、热负荷的预测误差［24］，电、热负荷概率密度函数分别为：

其中，μP和σP分别为电负荷有功功率P的期望和标准差；μΦ和σΦ分别为热负荷Φ的期望和标准差。

电负荷无功功率按定功率因数随有功功率变化。

3 基于Nataf变换和LHS的CLMCS方法

LHS 是一种分层采样的方法［17-19，25-26］，主要思想是通过产生更加均匀的样本来提高计算效率。传统LHS方法只针对输入随机变量相互独立的情况，为了处理输入随机变量之间的相关性，本文采用基于Nataf变换和LHS的CLMCS方法［17-19］，该方法具有以下特点：能给出输出随机变量的全面信息；能处理输入随机变量的相关性，且不受输入随机变量概率分布类型的约束；实现简单，稳健性好，结果精度高。

3.1 Nataf变换

设 n 维输入随机变量 X=（x1，x2，…，xn）T，其相关系数矩阵为CX。引入相关系数矩阵为CZ的n维标准正态分布随机变量 Z= （z1，z2，…，zn）T，根据等概率原则：

其中，Fk为xk的累积概率分布函数CDF（Cumulative Distribution Function）；ψk为 zk的 CDF。

CZ为正定矩阵，对其进行Cholesky分解可得下三角矩阵D，则n维独立标准正态分布随机变量Y=（y1，y2，…，yn）T为：

上述Nataf变换理论实现了从输入变量空间X到相关标准正态空间Z再到独立标准正态空间Y的转换，即式（16）和式（17）。因此，只要对独立标准正态分布随机变量Y进行N次采样得到样本矩阵Yn×N，利用 Nataf逆变换由式（17）得到相关标准正态分布随机变量Z的样本矩阵 Zn×N，再由式（16）就可以得到输入随机变量X的样本矩阵Xn×N。

为了实现上述转换，关键是确定相关系数矩阵CZ。对于CX和CZ对应元素之间的关系，文献［27］给出了几种常见分布的经验公式。J.M.Morales等学者首次将该方法应用到概率潮流的分析中［28］。尽管这些经验公式的精度很高，但是所支持的概率分布类型有限。对于服从Beta分布的光伏出力而言，缺乏可供参考的经验公式。为此，本文采用二维Nataf变换的方法，并与Gauss-Hermite积分相结合，得到相关系数矩阵CZ。该方法具有较高的精度，同时避免了无穷积分的计算，具体步骤参见文献［29］。

3.2 CLMCS方法

CLMCS方法主要包括采样和排序2个步骤。

a.采样。对n维任意分布的输入随机变量X=（x1，x2，…，xn）T进行 LHS，采样规模为 N，形成的样本矩阵为：

其中，uij为（0，1）均匀分布随机数。

b.排序。通过改变采样值的排列顺序，使样本矩阵的相关系数矩阵尽可能地接近CX，即将样本矩阵X′n×N的每一行元素按顺序矩阵 Ls重新进行排列，得到最终的样本矩阵 Xn×N。

由于F、ψ都是单调递增函数，因此，样本矩阵Xn×N和 Zn×N具有相同的顺序矩阵 Ls，即只要得到样本矩阵 Zn×N，就可以获得顺序矩阵 Ls［17-18］。

4 算法流程

本文首先建立了电-热互联综合能源系统稳态能量流模型，接着分析了系统中光伏出力和电、热负荷的概率分布，最后采用CLMCS方法定量评估P2H对电力系统和热力系统概率能量流的影响。本文所提方法的基本流程如图3所示。

图3 概率能量流算法流程Fig.3 Flowchart of probabilistic energy flow

5 算例分析

5.1 算例说明

本文测试算例为文献［7-8］中巴厘岛电-热互联综合能源系统，系统拓扑结构如图4所示。其中，电网为9节点配电网络，总有功负荷为1.6 MW；电网节点（6）接入2台分布式光伏发电机组，设每台机组的装机容量为0.5 MW，功率因数为1［18］，则本测试系统的光伏发电渗透率为38.5%；设Beta分布的形状参数为 α=β=0.9［18］。 热网为32节点环网，总热负荷为2.164 MW。电网和热网通过CHP机组和P2H元件（电锅炉）耦合，如表2所示。CHP1为定热电比燃气轮机，CHP2为变热电比抽气式汽轮机，CHP3为定热电比往复式内燃机。选取其中容量较大的CHP1和CHP2分别作为电网和热网的平衡节点。

图4 含光伏的巴厘岛电-热互联综合能源系统Fig.4 Integrated electricity-heat energy system with PV of Barry Island

表2 电网与热网耦合关系Table 2 Interdependence between electrical and heat networks

本文假设光伏出力和电、热负荷的期望为其预测值，标准差为期望的5%，并考虑以下3种相关性：同类型负荷之间的相关性，设电-电负荷、热-热负荷之间相关系数为0.7；不同类型负荷之间的相关性，设电-热负荷之间相关系数为0.5；光伏出力之间的相关性，设相关系数为0.8［18］。假设不同场景下各CHP机组的热电比恒定，需求量的变化全部由平衡节点承担。

综合考虑CLMCS方法的精度与效率，本测试算例采样规模设为2000。由于CLMCS方法的收敛过程具有波动性，为了保证计算结果准确可靠，在确定的采样规模下计算100次，取其平均值为最终结果。

5.2 P2H对系统概率能量流的影响

5.2.1 P2H对电力系统概率能量流的影响

光伏出力和电力系统负荷具有强随机性，有时不能满足电力系统的网络安全约束，尤其是当光伏出力达到峰值而电力系统负荷遭遇低谷，电力系统网络越限的概率显著提高。目前根据电力行业相关政策，一般通过弃光放弃一部分产能，以满足电力系统的网络安全约束。在含光伏的电-热互联综合能源系统中配置一定容量的P2H，相对于原来的弃光政策，可将部分电网难以消纳的光伏出力转化为热能。

电网节点（6）电压幅值的CDF随转化率v的变化如图5所示（图中电压幅值为标幺值）。转化率v定义为电锅炉消耗的有功功率与总光伏有功出力之比。当v=0（即没有配置电锅炉）时，电网节点（6）电压越限的概率超过60%。这种运行模式将直接导致大量弃光的产生。当v提高（即将部分电网难以消纳的光伏出力用于驱动电锅炉）时，电压越限的概率显著降低。当v提高到0.4时，电压越限的概率下降到20%以内。可见，在含光伏的电-热互联综合能源系统中配置一定容量的P2H，可以有效降低电网电压越限的概率，并为消纳弃光提供空间；另一方面，清洁可再生光伏发电的接入，可以减少系统的非可再生能源消耗，促进可再生能源系统的构建。

图5 P2H对节点（6）电压幅值的影响Fig.5 Impact of P2H on voltage magnitude of Node （6）

5.2.2 P2H对热力系统概率能量流的影响

热力系统负荷同样具有随机性，高峰热负荷期间，CHP机组将面临巨大压力。尤其是当电力系统负荷遭遇低谷，而热力系统负荷达到峰值时，仅仅依靠调整CHP机组的电热出力有时难以满足系统运行要求。利用电锅炉转化弃光所得的有效热出力就近平衡热网负荷，可以有效缓解热网压力。

热网管道流量随v的变化如图6（a）所示。随着v的提高，管道流量呈现下降趋势（尤其是重载管道）。以管道4为例，管道流量CDF随v的变化如图6（b）所示。v越高，管道流量标准差SD（Standard Deviation）越小，可有效避免管道过载。但部分轻载管道的SD可能随着v的增大而增大，如图6（c）所示。可见，P2H会将电网中的不确定性传播到热网，从而加剧部分轻载管道流量的波动；另一方面，P2H为热网带来额外的有效热输出，就近平衡热网负荷，改善了热网的潮流分布，从而可有效平抑重载管道流量的波动，并降低其越限风险。进一步地，由于P2H改善了热网潮流的分布，热网的损耗率也显著降低，如图7所示。

通过上述分析，P2H的配置促进了电-热互联综合能源系统安全、高效和经济运行。电网节点电压、热网管道流量随v的波动特性反映了网络安全约束对v的敏感程度。从这个意义上而言，P2H可作为系统潜在预防校正控制策略。通过调整系统的转化率v，可以更好地匹配分布式可再生光伏出力及电、热负荷的峰谷特性，提高系统抵御随机波动侵害的能力，增强系统的安全稳定性。另外，在电-热互联综合能源系统协同优化运行中，v也是保证系统经济安全运行的重要决策变量。

图6 P2H对管道流量的影响Fig.6 Impact of P2H on pipe mass flow rate

图7 P2H对热网损耗率的影响Fig.7 Impact of P2H on heat loss rate

5.3 电-热负荷相关性对系统概率能量流的影响

值得注意的是，在含光伏的电-热互联综合能源系统中，电、热负荷具有相关性，光伏出力的时空分布也具有相关性。更重要的是，在综合能源系统背景下，随着可再生分布式能源的进一步渗透，电力系统和热力系统的耦合不断加深，电、热相关性不容忽视。因此，有必要研究相关性对系统概率能量流的影响。

上述测试系统中电-热负荷相关系数ρeh为0.5。然而，随着系统运行条件和时空的转换，电-热负荷的相关程度也会有所波动。为分析ρeh对系统概率能量流的影响，本文设计了如下3种测试场景：场景1为 ρeh=0.3；场景 2为 ρeh=0.5，即上述测试算例；场景 3 为ρeh=0.7。

图8为电网节点（1）和节点（2）在不同测试场景下节点电压SD对比。由场景1到场景3，电压幅值的标准差逐渐增大。可见，相关性越强，电压波动越剧烈。因而，在含可再生分布式能源的综合能源系统概率能量流模型中应对随机变量之间的相关性予以充分考虑。同时，相关性越强意味着高峰电负荷和高峰热负荷同时出现的概率越高。因此，在确定电-热负荷的相关系数ρeh时，有必要适当参考电力系统和热力系统的历史负荷数据。

图8 测试场景1—3电网节点（1）和节点（2）电压 SDsFig.8 Voltage SDs of Node （1） and （2）for Case 1-3

6 结论

本文建立了含光伏的电-热互联综合能源系统概率能量流模型，采用CLMCS方法定量评估P2H对电力系统和热力系统概率能量流的影响，同时计及输入变量的随机性和相关性。所得结论如下。

a.P2H可以促进分布式可再生光伏的消纳及可再生能源系统的构建。

b.P2H可作为系统潜在的预防校正控制策略。通过调整系统的转化率v，可以更好地匹配光伏出力及电、热负荷的峰谷特性，增强系统的安全性，并促进电-热互联综合能源系统的协同优化运行。

c.随机变量相关性越强则系统波动越剧烈，因此，在含可再生分布式能源的综合能源系统概率能量流模型中应对随机变量之间的相关性予以考虑。

d.电-热互联综合能源系统概率能量流分析能够更全面地揭示综合能源系统的运行特性，从而为后续综合能源系统的规划、优化运行、风险评估等奠定基础。

参考文献：

［1］孙宏斌，郭庆来，潘昭光，等.能源互联网：驱动力、评述与展望［J］. 电网技术，2015，39（11）：3005-3013.SUN Hongbin，GUO Qinglai，PAN Zhaoguang，et al.Energy internet：driving force，review and outlook［J］.Power System Technology，2015，39（11）：3005-3013.

［2］邓建玲.能源互联网的概念及发展模式［J］.电力自动化设备，2016，36（3）：1-5.DENG Jianling.Concept of energy internet and its development modes［J］.Electric Power Automation Equipment，2016，36（3）：1-5.

［3］付学谦，孙宏斌，郭庆来，等.能源互联网供能质量综合评估［J］.电力自动化设备，2016，36（10）：1-7.FU Xueqian，SUN Hongbin，GUO Qinglai，et al.Comprehensive evaluation of energy quality for energy internet［J］.Electric Power Automation Equipment，2016，36（10）：1-7.

［4］王伟亮，王丹，贾宏杰，等.能源互联网背景下的典型区域综合能源系统稳态分析研究综述［J］. 中国电机工程学报，2016，36（12）：3292-3305.WANG Weiliang，WANG Dan，JIA Hongjie，etal.Review of steady-state analysis of typical regional integrated energy system underthe background of energy internet［J］.Proceedings of the CSEE，2016，36（12）：3292-3305.

［5］吴建中.欧洲综合能源系统发展的驱动与现状［J］.电力系统自动化，2016，40（5）：1-7.WU Jianzhong.Drivers and state-of-the-art of integrated energy systems in Europe［J］.Automation of Electric Power Systems，2016，40（5）：1-7.

［6］董今妮，孙宏斌，郭庆来，等.热电联合网络状态估计［J］.电网技术，2016，40（6）：1635-1641.DONG Jinni，SUN Hongbin，GUO Qinglai，et al.State estimation for combined electricity and heat networks［J］.Power System Technology，2016，40（6）：1635-1641.

［7］LIU X，WU J，JENKINS N，et al.Combined analysis of electricity and heat networks［J］.Applied Energy，2016，162：1238-1250.

［8］LIU X，JENKINS N，WU J，et al.Combined analysis of electricity and heat networks［D］.Cardiff，Britain：Cardiff University，2014.

［9］潘昭光，孙宏斌，郭庆来.面向能源互联网的多能流静态安全分析方法［J］. 电网技术，2016，40（6）：1627-1634.PAN Zhaoguang，SUN Hongbin，GUO Qinglai.Energyinternet oriented static security analysis method for multi-energy flow［J］.Power System Technology，2016，40（6）：1627-1634.

［10］顾泽鹏，康重庆，陈新宇，等.考虑热网约束的电热能源集成系统运行优化及其风电消纳效益分析［J］.中国电机工程学报，2015，35（14）：3596-3604.GU Zepeng，KANG Chongqing，CHEN Xinyu，et al.Operation optimization of integrated power and heat energy systems and the benefit on wind power accommodation considering heating network constraints［J］.Proceedings of the CSEE，2015，35（14）：3596-3604.

［11］BORNAPOUR M，HOOSHMAND R A，KHODABAKHSHIAN A，et al.Optimal coordinated scheduling of combined heat and powerfuelcell，wind，and photovoltaicunitsin microgrids considering uncertainties［J］.Energy，2016，117：176-189.

［12］舒印彪，张智刚，郭剑波，等.新能源消纳关键因素分析及解决措施研究［J］. 中国电机工程学报，2017，37（1）：1-8.SHU Yinbiao，ZHANG Zhigang，GUO Jianbo，et al.Study on key factors and solution of renewable energy accommodation［J］.Proceedings of the CSEE，2017，37（1）：1-8.

［13］SALPAKARI J，MIKKOLA J，LUND P D.Improved flexibility with large-scalevariablerenewablepowerin citiesthrough optimal demand side management and power-to-heat conversion［J］.Energy Conversion&Management，2016，126：649-661.

［14］LUND H，MÖLLER B，MATHIESEN B V，et al.The role of district heating in future renewable energy systems［J］.Energy，2010，35：1381-1390.

［15］BÖTTGER D，GÖTZ M，THEOFILIDI M，et al.Control power provision with power-to-heat plants in systems with high shares of renewable energy sources-an illustrative analysis for Germany based on the use of electric boilers in district heating grids［J］.Energy，2015，82：157-167.

［16］LI J，FANG J，ZENG Q，et al.Optimal operation of the integrated electrical and heating systems to accommodate the intermittent renewable sources［J］.Applied Energy，2016，167：244-254.

［17］陈雁，文劲宇，程时杰.考虑输入变量相关性的概率潮流计算方法［J］. 中国电机工程学报，2011，31（22）：80-87.CHEN Yan，WEN Jinyu，CHENG Shijie.Probabilistic load flow analysis considering dependencies among input random variables［J］.Proceedings of the CSEE，2011，31（22）：80-87.

［18］CHEN Y，WEN J，CHENG S.Probabilistic load flow method based on Nataf transformation and Latin hypercube sampling［J］.IEEE Transactionson Sustainable Energy，2013，4（2）：294-301.

［19］黄煜，徐青山，卞海红，等.基于拉丁超立方采样技术的半不变量法随机潮流计算［J］. 电力自动化设备，2016，36（11）：112-119.HUANG Yu，XU Qingshan，BIAN Haihong，etal.Cumulant method based on Latin hypercube samplingforcalculating probabilistic power flow［J］.Electric Power Automation Equipment，2016，36（11）：112-119.

［20］李正茂，张峰，梁军，等.含电热联合系统的微电网运行优化［J］.中国电机工程学报，2015，35（14）：3569-3576.LI Zhengmao，ZHANG Feng，LIANG Jun，et al.Optimization on microgrid with combined heat and power system［J］.Proceedings of the CSEE，2015，35（14）：3569-3576.

［21］BLARKE M B.Towards an intermittency-friendly energy system：comparing electric boilers and heatpumps in distributed cogeneration［J］.Applied Energy，2012，91：349-365.

［22］王敏.分布式电源的概率建模及其对电力系统的影响［D］.合肥：合肥工业大学，2010.WANG Min.The probabilistic modeling of distributed generation and its influences on power systems［D］.Hefei：Hefei University of Technology，2010.

［23］陈璨，吴文传，张伯明，等.考虑光伏出力相关性的配电网概率潮流［J］. 电力系统自动化，2015，39（9）：41-47.CHEN Can，WU Wenchuan，ZHANG Boming，et al.Probabilistic load flow of distribution network considering correlated photovoltaic power output［J］.Automation of Electric Power Systems，2015，39（9）：41-47.

［24］陈胜，卫志农，孙国强，等.电-气混联综合能源系统概率能量流分析［J］. 中国电机工程学报，2015，35（24）：6331-6340.CHEN Sheng，WEI Zhinong，SUN Guoqiang，et al.Probabilistic energy flow analysis in integrated electricity and natural-gas energy systems［J］.Proceedings of the CSEE，2015，35（24）：6331-6340.

［25］YU H，CHUNG C Y，WONG K P，et al.Probabilistic load flow evaluation with hybrid Latin hypercube sampling and Cholesky decomposition［J］.IEEE Transactions on Power Systems，2009，24（2）：661-667.

［26］WEI Z，CHEN S，SUN G，et al.Probabilistic available transfer capability calculation considering static security constraints and uncertainties ofelectricity-gasintegrated energy systems［J］.Applied Energy，2016，167：305-316.

［27］LIU P L，KIUREGHIAN A D.Multivariate distribution models with prescribed marginals and covariances［J］.Probabilistic Engineering Mechanics，1986，1（2）：105-112.

［28］MORALES J M，BARINGO L，CONEJO A J，et al.Probabilistic power flow with correlated wind sources［J］.IET Generation Transmission&Distribution，2010，4（5）：641-651.

［29］LI H S，LÜ Z Z，YUAN X K.Nataf transformation based point estimate method［J］.Science Bulletin，2008，53（17）：2586-2592.