一种改进的表面重建算法及其并行化研究

王元+曹静+娄泽坤

摘 要： 对于泊松三维表面重建中估算指示函数出现误差的情况，引入屏蔽因子并使用线性插值的方法纠正误差。该方法在等值面提取时使用的索引表查找法存在二义性的问题，需使用渐近线方法来解决。改进算法需要较大的存储空间来存储顶点信息和法向量以及较长的时间来运算，因而引入了CUDA架构的并行化计算来提高运行效率。

关键词： 多视图三维重建； 泊松表面重建； 二义性； CUDA架构

中图分类号：TP391 文献标志码：A 文章编号：1006-8228（2017）05-17-03

An improved 3D surface reconstruction method and it's parallelization

Wang Yuan， Cao Jing， Lou Zekun

（School of Computer and Information Engineering， Henan University， Kaifeng， Henan 475000， China）

Abstract： In this thesis the shielding factor is introduced to solve the problem of errors of indication function to estimate the indicator function in the Poisson surface reconstruction algorithm. In the part of isosurface extraction in surface reconstruction， the triangulation process is performed by searching the index table. But this method will lead to ambiguity， so an asymptotic method is used to avoid it. This surface reconstruction algorithm will improve the holes and depressions problems of complex objects. At the same time， it leads to larger storage space to store vertex and normal vectors， and a longer time to process data. Therefore， CUDA architecture and parallelization are introduced to solve the problem of efficiency.

Key words： multi view 3D reconstruction； Poisson surface reconstruction； ambiguity； CUDA architecture

0 引言

2006年，Michael Kazhdan等人提出了泊松表面重建算法[1]，但泊松表面重建本身存在諸多缺陷。如该算法在矫正指示函数的时候使用的是一次性全局的偏移[2]。若在实际的实现过程中出现计算指示函数不可避免的误差，此时再用一次性全局偏移的方法估算指示函数则会出现重建结果误差较大的情况[3]；另外等值面提取部分用移动立方体算法，该算法通过索引表查找各个体素内三角面片的连接模式确定等值面的分布方式，但是索引表算法会产生连接二义性问题。

鉴于第一个问题，最主要的突破口是找到一个合适的全局偏移量来解指示函数的近似解，本文尝试使用显性插值方法对样本点进行插值计算。对于存在连接二义性的情况，改进方法是渐近线算法。同时对改进之后算法的效率提升问题引入支持计算统一设备架构（CUDA），采用GPU并行计算，其存储器带宽和并行处理能力有CPU处理无法逾越的优势。

1 引入屏蔽因子和渐近线算法的表面重建

1.1 引入屏蔽因子

在泊松方程的求解过程中[5]，对于目的有向点集求解尺度指示函数，使尺度函数的梯度与有向点集形成最佳逼近即尺度函数最小化问题

在此，本文给定带权重的点集，为尺度函数最小化增加一些约束重新计算样本点函数，见公式⑵：

其中Area（S）是要重建的表面区域，α是一个权值，用来衡量拟合梯度和拟合值，也可叫做屏蔽因子，w（p）是样本点权重，在该算法实现中，根据局部采样密度估计得到表面区域，每个样本点的权重w（p）设置为1。上述公式简化为公式⑶：

表示单位体素在函数空间上的表示形式，这个值是由采样点的函数加权和得到的，见公式⑷：

公式⑷将梯度约束和离散点约束值整合进空间域，随即指示函数的方程最小化为或者。

此时，若指示函数满足，则此等式就是屏蔽泊松方程。

通过引入屏蔽因子解屏蔽泊松方程的方法，使用显性插值计算，解决一次性全局估算指示函数误差较大的情况。

1.2 使用渐进性方法解决二义性

移动立方体算法提供了以查找索引表的方式确定体素内等值面的连接方式，但这种方法也过于依赖直观的构造，忽略了构造三角面片时可能存在的二义性问题。如图1，在立方体体素的某一等值面上若出现对角线的两端同时为+，另一对角线两端同时为-的情况时，不同的连接方式会构造不同的结果，如图1。

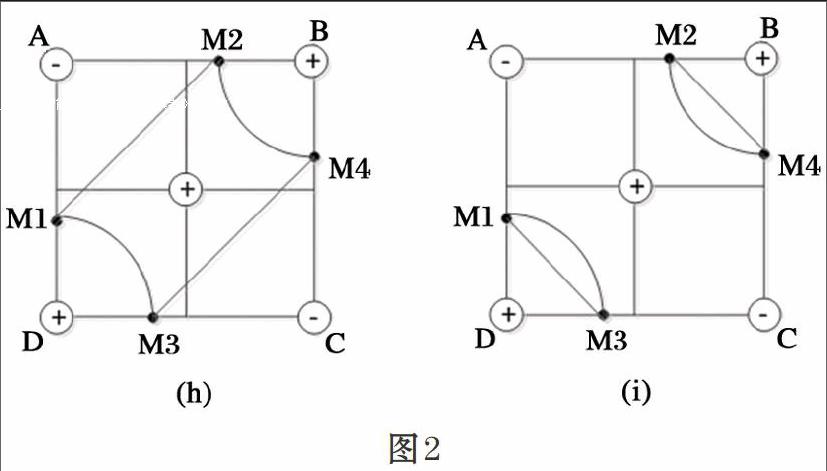
对于存在连接二义性的情况改进方法是渐近线算法，通过边界面与等值面相交的理论得知，二者相交的结果是一对双曲线，计算双曲线的渐近线，通过双曲线、双曲线的渐近线与体素边界面三种体元的位置关系来判断是否产生二义性，对于有面二义性的情况，做渐近线处理判别方法，作图2（h）和（i）：

当顶点为+和顶点为-分别出现在一对对角线两端时出现连接二义性，此时若渐近线交点为+如图2（h），则渐近线交点和B点D点处于同一区域，此时等值点M1和M2连接，M3和M4连接；若渐近线交点为-如图2（i），则渐近线交点和A点C点处于同一区域，此时等值点M1和M3连接，M2和M4连接。

2 关于改进表面重建算法的GPU并行优化

从CUDA架构可知，CUDA并行算法的设计需要程序的数据相互独立，在实现的过程中需要处理若干相互不相干的子问题[4]，这些子问题被分割放置在每一个kernel函数中同时执行，对于八叉树结构每个深度层次上的数据计算可用CUDA架构并行化处理，可根据串行程序中耗时不同设计并行算法。

根据程序耗时分析，设计数据离散化八叉树生成部分进行GPU并行计算[6-7]。

2.1 包围盒的并行计算

包围盒，可作为八叉树的根节点，计算各个样本点的相对位置。在我们的并行设计算法中，处理并行计算包围盒用的是CUDPP的方法，CUDPP是一种强大的数据并行CUDA库。

CUDPP的具体调用过程如下。

⑴ 初始化，调用cudppCreate实例化一个CUDPP，生成一个CUDPPManager对象，将其地址返回给theCudpp。

⑵ 为主机端和设备端使用函数分配存储空间，对主机端所要输入参数集赋值。

⑶ 将数据从主机端复制到设备端指定的存储空间，使用cudaMemcpy2D（）函数进行主机端与设备端之间的二维数据传输。数据传输方向是主机端到设备端，cudaMemcpyHostToDevice（）。

⑷ 生成“CUDPP计划”。CUDPP计划是CUDPP方法中特有的一部分内容，具体做法是定义一个CUDPPHandle，生成一个cudppPlan将句柄赋值给scanPlan。

⑸ 執行原语。

在CUDPP计划配置参数完成之后即要开始执行这一过程的kernel函数。最后，用cudaThreadSynchronize（）函数同步处理。

⑹ 将输出数据复制到主机端。继续由主机端执行逻辑控制。依然使用函数cudaMemcpy2D（）进行拷贝，数据传输方向是设备端到主机端cudaMemcpyDeviceToHost（）。

⑺ 所有处理完成之后释放所分配的存储空间。

2.2 生成键值序列及键值排序并行算法设计

键值序列在树形数据结构中表节点的权值，也代表了多维空间中数据的表达方式，计算键值序列的基础是计算莫顿码（Morton码）[8]。

在八叉树的数据结构中给定一个采样点p，在d层（1<=d<=D）计算p的键值序列xyz，以及为键值序列排序。分别计算键值xd、yd、zd，定义Cdx为d-1层包含p点的节点Od-1的形心，p.x为采样点p相对于形心的位置，若p.x位于节点Od-1的x轴平分线的左侧，x键值为0，否则为1；y键值和z键值也以同样的方法计算。

如此，深度为D的八叉树键值序列表示为x1y1z1x2y2z2…xDyDzD，意义为从根节点到当前节点的路径。但由于输入点云数据是乱序的，由此生成的每个节点的键值序列也有可能是乱序的，还需对键值序列进行排序，可以使用CUDPP库sort方法处理所生成的键值序列。

2.3 生成节点数组并生成完整八叉树结构

由于八叉树结构的每一个节点都有0个孩子节点或7个孩子节点，因此需要对生成的惟一节点数组补全剩余的7个节点数组信息。首先需要计算其余7个节点数组的起始索引地址，使用scan算法并行计算前缀求和的方法在上一个节点数组地址基础上计算邻接的节点数组地址，得到完整的八叉树节点数组地址。

3 仿真结果

实验所需输入点云数据是所参与项目中使用的古建筑点云数据集jyd.ply。

使用改进过的表面重建算法，生成结果与原始算法结果对比截图如图3。

图3左为jyd原始表面重建算法的重建结果，图3右为本章改进算法的重建结果，从图中可看出屋脊边缘部分的孔洞问题得到解决。

分别使用这两组数据串行计算和并行计算实验三次，结果如表1。

根据表格中数据可知jyd三次的加速比分别为6.05、5.98、5.78，平均为5.93。

4 结论

通过引入屏蔽因子使用显性插值方法对样本点进行插值计算，避免了一次性全局偏移的方法估算指示函数出现重建结果误差较大的情况，通过引入渐近线构造等值线正确连接方式的方法，避免了移动立方体算法中三角化过程可能出现的面二义性问题。实验结果证明，改进的表面重建算法，可改善模型表面空洞问题。

同时并行算法设计方案实验结果证明GPU并行算法提高了原有表面重建算法的执行效率。

参考文献（References）：

[1] Lin Y， Chen C， Song M， et al. Dual-RBF based surface reconstruction[J]. The Visual Computer，2009.25（5-7）：599-607

[2] Li X， Wan W， Cheng X， et al. An improved poisson surface reconstruction algorithm[C]. International Conference on. IEEE，2010：1134-1138

[3] Yin C， Gang D， Zhi-quan C， et al. An algorithm of CUDA-based Poisson surface reconstruction[C]. Audio Language and Image Processing （ICALIP）， 2010 International Conference on，2010：203-207

[4] Zhou K， Gong M， Huang X， et al. Data-parallel octrees for surface reconstruction[J]. Visualization and Computer Graphics， IEEE Transactions on，2011.17（5）：669-681

[5] 陈建华，赵飞，葛永斌.求解3维泊松方程的一种新方法[J].江西师范大学学报（自然科学版），2013.4：411-415

[6] 游安军编著.电路数学[M].北京电子工业出版社，2014.

[7] 蒋建刚.薛定谔和泊松方程有限元法求解[D].广东工业大学硕士学位论文，2014.

[8] 杨宇，阚凌雁，于佳，等.基于激光扫描的人脸三维重建方法[J].红外与激光工程，2014.12：3946-3950