特高压换流站内电压变送器中铁磁材料励磁曲线拟合方法研究
叶有名,唐 明,张 华,陈 刚
(1.国网四川省电力公司,四川 成都 610041;2.国网四川省电力公司电力科学研究院,四川 成都 610072)
特高压换流站内电压变送器中铁磁材料励磁曲线拟合方法研究
叶有名1,唐 明2,张 华2,陈 刚2
(1.国网四川省电力公司,四川 成都 610041;2.国网四川省电力公司电力科学研究院,四川 成都 610072)
研究了特高压换流站中由交直流耦合引发的铁磁谐振过电压问题,针对套管末屏测量单元中电压变送器的励磁曲线特性,分析了奇次多项式拟合与正切函数拟合的特点。利用泰勒公式与伯努利函数等数学工具论证了二者的拟合特具有内在统一性,为铁磁谐振非线性方程的各种解析解和数值提供了理论支撑。
特高压;铁磁谐振;伯努利函数
0 引 言
随着中国西部大开发战略以及新能源战略的扎实推进和不断深入,“十三五”末四川电网水电外送能力预计超过60 Gw,其中通过超特高压直流输电工程外送的电力接近50 Gw,占到总外送能力的80%左右。在此期间,西南+两华异步电网格局也将逐步形成,以四川为中心的西南电网特性将发生巨大改变,直流输电运行特性及其扰动的实时控制、响应特性将对电网运行产生越来越显著的影响。预计至2025年,四川电网内可能将再建10条以上的直流输电工程,直流输电系统运行性能和可靠性将对四川电网和交直流混联电网安全运行起到至关重要的作用。
虽然中国在特高压直流输电技术领域已经达到国际领先水平,但近年来的特高压运维经验表明,在直流输电的诸多细节方面仍有大量的研究工作有待深入开展。其中,交流系统和直流系统之间的耦合以及引发的铁磁谐振过电压问题尤为突出,其电磁暂态过程机理复杂,对特高压直流输电工程的安全稳定运行构成很大威胁。
在铁磁谐振领域,人们做了大量的研究;但由于铁磁谐振问题理论上属于高阶非线性系统[1],无法得到数学上的解析解,因此对问题的本质还未完全搞清楚。大量的试验研究和运行均表明,实际的谐振情况十分复杂,可能存在基频、高频和分频谐振甚至混沌等不同的谐振状态[2],因此长期以来铁磁谐振一直是内部过电压的理论难题和实际难题。
在理论分析上,主要有图解法、相平面法、谐波平衡法、描述函数法等[3-5]。在数值计算和仿真分析方面,用给定参数进行计算得出有关谐振的规律,或者是采用电力系统电磁暂态计算程序对实际系统进行建模仿真计算。
20世纪80年代后期,学者们又将铁磁谐振与非线性动态系统和混沌分析结合起来[6],将分叉理论、奇异和非奇异吸引子的概念引入铁磁谐振的研究领域[7],利用功率谱密度和庞加莱映射等方法对其进行动态分析[8]。
但无论是求近似解析解还是数值解,励磁曲线的获取和精确拟合是最核心的问题。在忽略磁滞和涡流的前提下,常见的励磁曲线拟合方法有奇次多项式拟合与反正切函数拟合等方法。这里重点研究这两种拟合方法各自的特点,并论证二者在数学本质上的统一性。
1 换流变压器套管末屏铁磁谐振的非线性方程
特高压换流站换流变压器套管末屏分压器是监测阀侧绕组电压的重要节点,其所采用的电容分压原理与后续电压采集单元构成了典型的CVT结构。为方便研究,可以采用戴维南定理将其等效转化成如图1所示的RLC串联电路。
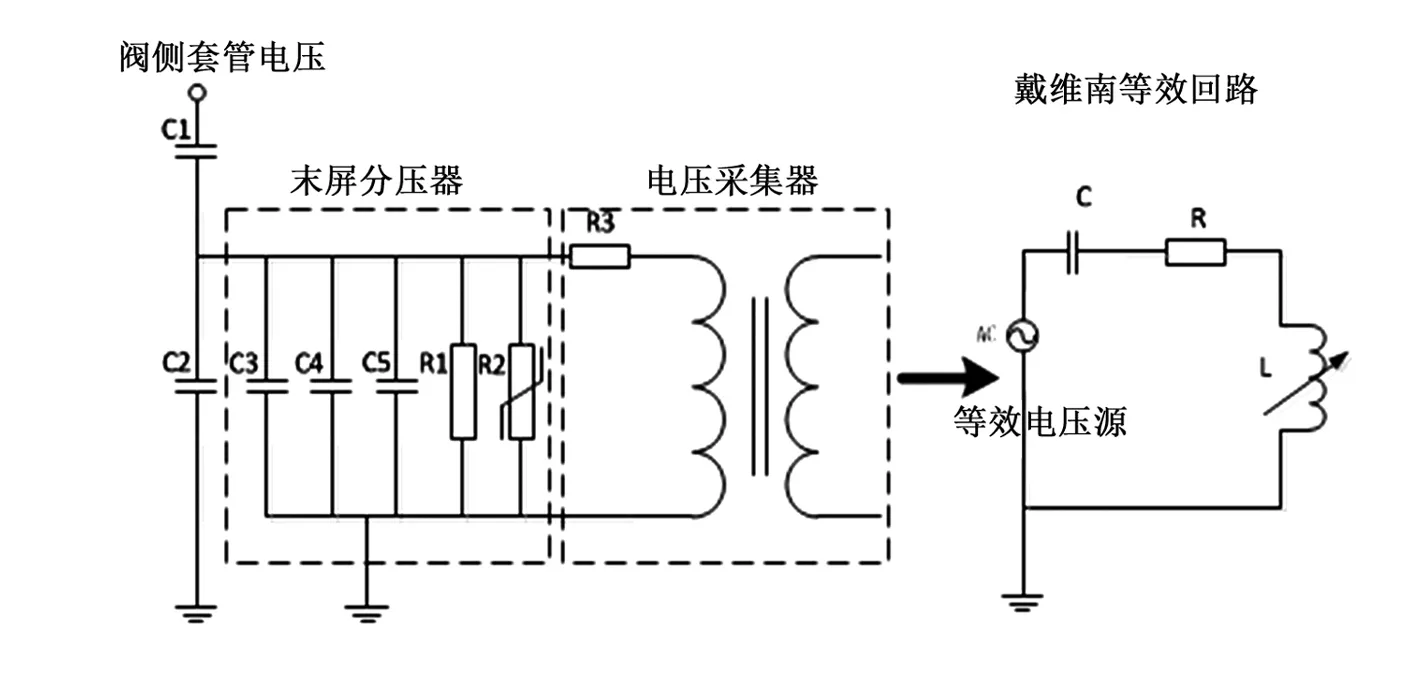
图1 末屏分压器的戴维南等效电路图
该等效电路为一典型的串联RLC电路,其回路电压方程为
(1)
式中:E为等效电压源电动势;i为回路中的电流;R为串联电阻;C为等效电容;φ为铁心主磁链。
将i=f(φ)代入末屏分压器回路电磁方程中可得
(2)
取E=Emsin(ωt),对式(2)两边求导可得
(3)
式(3)是二阶非线性方程,且带有恒频恒幅激励项。结合实际励磁曲线进行拟合之后,可以方便地得到f(φ)中各多项式的系数。但即便如此,该方程也无法得到解析解。在不同的参数下,结果可能存在周期响应、拟周期响应甚至混沌响应,且不同初始条件对解的形式影响很大。
2 励磁曲线拟合方法的统一性证明
在考虑铁心的饱和之后,其磁链和励磁电流之间不再是简单的线性关系,某特高压换流站中换流变压器套管末屏电压采集器的励磁曲线如图2所示。
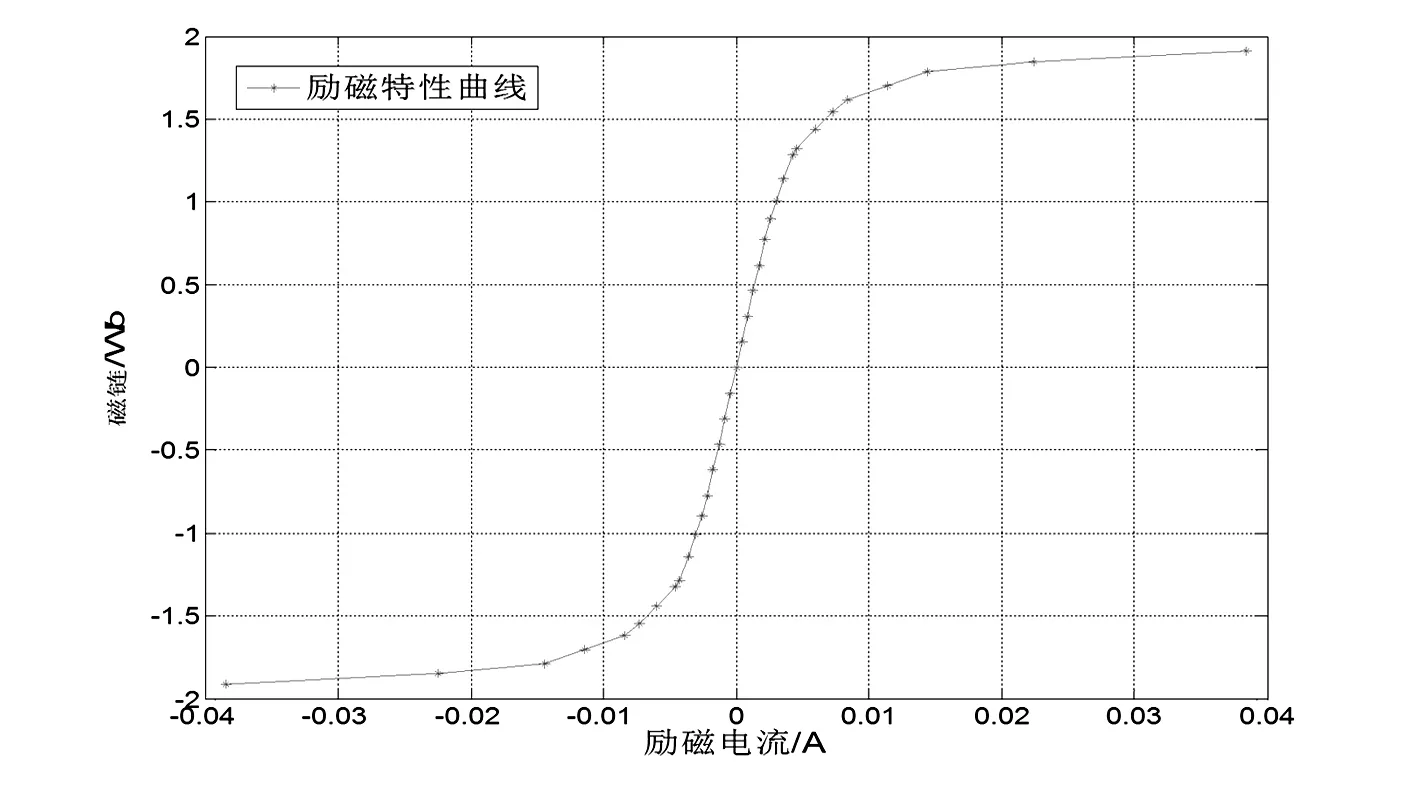
图2 电压采集器的励磁曲线
不失一般性,定义电流和磁链之间的关系为
i=f(φ)
(4)
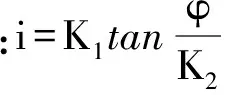
在不考虑磁滞、涡流的情况下,铁磁材料的励磁曲线i=f(φ)是一条过原点的单调递增曲线,具有奇对称的性质,且满足狄利克雷条件。在(0,0)点对其进行泰勒展开:
(5)
式中,Rn(φ)为φn的高阶无穷小。
由i=f(φ)的奇对称特性可知,其泰勒展开的无穷级数中只有φ的奇次幂而没有偶次幂,且f(0)=0,因此i=f(φ)的泰勒级数展开可以化简为
(6)
因此,对于i=a1φ+a3φ3、i=a1φ+a5φ5、i=a1φ+a7φ7、i=a1φ+a3φ3+a5φ5等拟合方法,均是励磁曲线i=f(φ)在某种程度上的截断和近似,其精度仅在某些范围内满足工程要求。
正、余弦函数的麦克劳林级数为
(7)
(8)
式中,R2n(φ)为φn的高阶无穷小。
则正切函数泰勒展开可以由式(9)计算:
(9)
采用多项式相除常见的“长除法”,对式(9)进行化简可得
(10)
式中,Bn为n次伯努利数,可以通过递推公式进行计算。
(11)
于是正切函数的泰勒展开可以表达为
(12)
由上面推导可见,tanφ函数其本身的泰勒展开即为无穷项奇次幂多项式的加权之和,用其对励磁曲线进行拟合在精度上必然要高于有限项奇次多项式的拟合结果,这是由正切函数本身的性质所决定。
上述结果表明,励磁特性曲线i=f(φ)为一满足狄利克雷条件的单调递增奇函数,因此可以展开为奇次幂多项式无穷级数的加权之和。各类文献中关于i=f(φ)函数关系式的各种拟合方法具有内在的统一性,均是奇次幂多项式的叠加;但采用正切函数进行拟合时,由于其本身就是奇次幂多项式的无穷级数之和,因此拟合效果会明显优于有限项多项式的拟合效果。
3 总 结
特高压换流站中由交直流系统间的耦合而引发的铁磁谐振过电压问题尚不多见:由于铁磁材料的饱和特性所引进的非线性特点,以至于无法得到解析解,在求取其数值解的时候,对励磁曲线的近似拟合十分关键。
前面探讨了常见的两种拟合方法,并通过泰勒公式和伯努利函数等数学工具论证了两种拟合方法在本质上是一致的。可以认为,采用有限项多项式对励磁曲线进行拟合是采用正切函数进行拟合的子集。从励磁特性曲线本身的泰勒展开表达式上讲,两类方法具有高度的统一性。
[1] 杨鸣. 铁磁谐振过电压非线性特性及其柔性抑制策略研究[D].重庆:重庆大学,2014.
[2] 刘凡. 中性点直接接地系统铁磁谐振过电压的混沌特性与控制检测方法[D]. 重庆:重庆大学,2006.
[3] 李俊. 500kVCVT铁磁谐振问题研究[J]. 电测与仪表,2010,47(7A):65-68.
[4] 张业. 电力系统铁磁谐振过电压研究[D].成都:西南交通大学,2008.
[5] 秦祖泽,黄绍平. 电容式电压互感器分频铁磁谐振新的分析方法[J]. 高压电器,1997(4):19-22.
[6] 王世凯. 小电流接地电力系统铁磁谐振消谐装置的研究[D].呼和浩特:内蒙古工业大学,2007.
[7] 张博,鲁铁成,杜晓磊. 中性点接地系统铁磁谐振非线性动力学分析[J].高电压技术,2007,33(1):31-35.
[8] 黄治国,雷红才,苗青,等.电容式电压互感器分频谐振的分析与对策[J]. 高电压工程,2004,30(7):58-59.
国家电网公司面向社会各界征集新技术
国家电网公司贯彻落实国家创新驱动发展战略,致力于推动电力新技术在电网建设、生产、运营中的推广应用工作。现诚邀社会各界通过新技术征集平台(国家电网公司电子商务平台http://ecp.sgcc.com.cn)开展新技术申报工作。
Ferroresonance over-voltage caused by coupling of AC and DC system in ultra-high voltage (UHV) converter station is studied. Based on the excitation curve in voltage transformer unit, both characteristics of odd order polynomial fitting and tangent function fitting are analyzed and compared. Taylor′s formula and Bernoulli function are induced to prove the unity of both fitting methods, which provides a theoretical foundation for analytic solution and numerical solution.
ultra-high voltage; ferroresonance; Bernoulli function
TM713
A
1003-6954(2017)02-0001-03
2016-11-08)
叶有名(1972),硕士,高级工程师,研究方向为电力系统自动化、高压直流输电。
唐 明(1986),博士、工程师,主要从事电力系统稳定分析与控制的研究。

