鸡兔同笼问题各种解法的联系
摘 要:鸡兔同笼是数学界经典问题,以解法策略的多样性凸显其魅力,有算术的巧算法和代数的方程方法,本文列举解决鸡兔同笼的解法,分析解题策略,探索各种方法之间内在联系。
关键词:鸡兔同笼;解法
鸡兔同笼是中国古代的数学名题之一。大约在1500年前,《孙子算经》中就记载了这个有趣的问题。书中是这样叙述的:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”这四句话的意思是:有若干只鸡兔同在一个笼子里,从上面数,有35个头,从下面数,有94只脚。问笼中各有几只鸡和兔?
日本有“龟鹤算题”,例如:“龟鹤合计共10只,共有28條腿,问龟鹤各有多少只?”就是从中国古代的“鸡兔同笼”问题演变来的。
仔细想想就知道,这是一种脱离生活实际的空想问题。因为鸡和兔(或龟与鹤)是完全不同的动物,数总数时自然会知道会有几只鸡、几只兔。由于它们的脚也长得完全不同,故在数总数时,知道其各自是多少也不会错。因此,这个问题仅仅是作为一种智力测验的问题。
“鸡兔同笼”问题之所以成为数学名题,魅力在于解决问题策略的多样性,体现思维的灵活性、创造性,从不同解法还可发现数学的发展(算术到代数),体会数学的解放感及力量感(张景中语)。
许多小学算术应用题都可以转化成这类问题, 用解它的典型解法来求解。到中学的方程中也是典型问题,近几年国家公务员考试对这类问题也有考查,因此学会它的解法和思路很重要。
本文列举解决鸡兔同笼的解法,分析解题策略,探索各种方法之间内在联系。
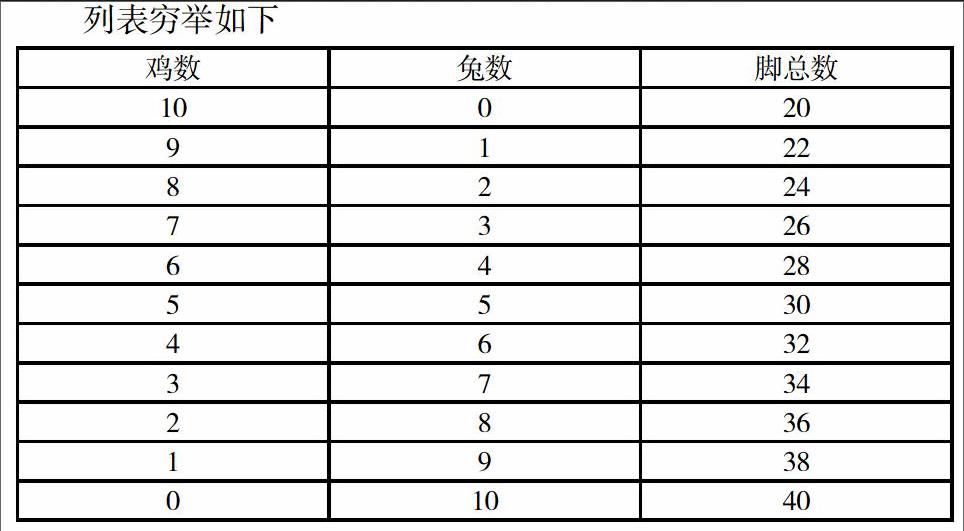
解决方法一:列表穷举法
原题数较大,根据化繁为简的思想方法,可从简单的问题入手,先研究“有若干只鸡兔同在一个笼子里,从上面数,有10个头,从下面数,有28只脚。问笼中各有几只鸡和兔?
从这张表可以看出,脚的总数为28时,有6只鸡,4只兔,即为答案。
当然,在具体列表解决时,只用列到第5行,脚总数与题吻合。
这是一种原始的、一步一步纠正错误的方法,用试探错误的方法解决。思维含量较低,适合低年级儿童。目前,鸡兔同笼问题已进入小学四年级教材,解决时,就是用列表运用尝试的办法探索规律,得出结果,使学生感受这是数学探索的一种有效途径。
但若数字较大的话,要画这张表就太费事了。例如原题(35头,94足),这张表要列到35行,工作量很大!效率低。因此,应当寻求更好的解决方法。
解决方法二:假设法
观察表中所列脚总数可知,它是每次2只递增的。这是因为每次是以4只脚的兔来替换2只脚的鸡的缘故。10只鸡、0只兔时有20只脚,由此要变成28只脚就必须增加8只脚。据此8÷2=4, 应将4只鸡转换成兔。我们可将这种思考方法称为假设法。
假设法————假设都是鸡
(1)如果笼子里都是鸡,那么就有10×2=20只脚。
(2)多出 28—20=8。
(3)一只兔比一只鸡多2只脚,也就是有8÷(4—2)=4只兔。
(4)所以笼子里有6只鸡、4只兔。
用此方法,即使数字较大,也不难解了。
比如回到原题(35头,94足),如果笼子里都是鸡,说的生动些,不防可以假设先让兔子都抬起2只脚,那么现在就有35×2=70只脚,现在的脚数和原来差94-70=24只脚,这些都是每只兔子抬起2只脚,一共抬起24只脚,用24÷2得到兔子有12只,用35-12得到鸡有23只。
兔子站起——想得活!
假设法————假设都是兔
把每只鸡的两个翅膀也当作脚,那么每只鸡就有4只脚,与兔的脚数相同,则鸡兔共有脚35×4=140只,多了140-94=46只脚,这就是鸡的翅膀数,所以鸡有46÷2=23只,兔有35-23=12只。
把鸡翅膀当作脚——想得妙!
假设法————抬脚法1
假如让鸡抬起一只脚,兔子抬起2只脚,还有94÷2=47(只)脚。笼子里的兔就比鸡的脚数多1倍,这时,脚与头的总数之差47-35=12,就是兔子的只数。
金鸡独立,兔子站起——想得巧!
假设法————抬脚法2
假如鸡与兔子都抬起两只脚,还剩下94-35×2=24只脚 , 这时 地上只有兔子的脚,而且每只兔子有两只脚在地上,所以有24÷2=12只兔子,就有35-12=23只鸡。
让鸡飞起来,兔子站起——想得绝!
不管怎么说,从前的这种鸡兔同笼仍属一种较困难的计算题。
解决方法三:代数方程法
然而这种从前鸡兔同笼难题,随着数学的发展,若用代数方程这种新式武器来解决,就方便多了。用代数方程既可以用一元一次方程也可以用二元一次方程组解决。
一元一次方程
解:设兔有x只,则鸡有(35-x)只。
4x+2(35-x)=94
4x+70-2x=94
(4-2)x=94
2x=94-70
2x=24
x=24÷2
x=12
35-12=23(只)
由上可见,这里出现的94-70与之前假设法相同,把它用4-2来除也与之前相同,而 35×2的出现是理所当然的,这不就是假设先让兔子都抬起2只脚后, 现在就有的35×2=70只脚吗?
或 解:设鸡有x只,则兔有(35-x)只。
2x+4(35-x)=94
2x+140-4x=94
2x=46
x=23
35-23=12(只)
答:兔子有12只,鸡有23只。
二元一次方程组
解:设兔有x只,鸡有y只。
x+y=35 ①
4x+2y=94 ②
解二元一次方程组有代入法、加减法,以下列出各种解法,再看看与之前解法的联系。
代入法:
由①得:y=35-x ③
把③代入 ② 得:4x+2(35-x)=94
4x+70-2x=94
(4-2)x=94
2x=94-70
2x=24
x=24÷2
x=12
35-12=23(只)
答:兔子有12只,鸡有23只。
可看出此种解法消元后与一元一次方程解法一致。
加减法
法1: ①×4得:4x+4y=35×4=140 ③【假设都是兔,则鸡兔共有脚35×4=140只】
③- ② 4y-2y=140-94【多了140-94=46只脚,这就是鸡的翅膀数】
2y=46
Y=46÷2
Y=23
把Y=23 代入① 得:x=12
∴ x=12 Y=23
可看出这就是巧算法中的“把鸡翅膀当作脚”法
法2:①×2得:2x+2y=35×2=70 ③
②- ③ 4x-2x=94-70【假如鸡与兔子都抬起两只脚,还剩下94-35×2=24只脚】
2x=24
x=24÷2 【每只兔子有两只脚在地上,所以有24÷2=12只兔子】
x=12
代回①得:Y=23
可看出这就是巧算法中的“让鸡飞起来,兔子站起”法。
法2:①×2得:2x+2y=35×2=70 ③【 先让兔子都抬起2只脚, 现在就有35×2=70只脚】
②- ③ 4x-2x=94-70【現在的脚数和原来差94-70=24只脚, 兔子一共抬起24只脚 】
2x=24
x=24÷2 【每只兔子抬起2只脚,用24÷2得到兔子有12只】
x=12
代回①得:Y=23
可看出这就是巧算法中的“兔子站起”法。
法3: ②÷2 得:2x+y=94÷2=47 ③ 【鸡抬起一只脚,兔子抬起2只脚,还有94÷2=47(只)】
③ - ①得:2x- x=47-35 【脚与头的总数之差47-35=12,就是兔子的只数】
x=12
代回①得:Y=23
可看出这就是巧算法中的“金鸡独立”法。
综上所述,鸡兔同笼问题解决的方法很多,从列举、算术巧算到代数方法,这些不同的方法策略所展现的魅力,正是这个问题流传到国外、从古流传至今,成为经典的原因!各种巧妙方法,令古今中外数学家赞叹不已。这种思维方法叫化归法。化归法就是在解决问题时,先不对问题采取直接的分析,而是将题中的条件或问题进行变形,使之转化,直到最终把它归成某个已经解决的问题。数学是思维的科学,数学教学是思维的教学——数学对于发展学生的思维是至关重要的,问题是数学的心脏,鸡兔同笼问题是一经典!
同时,通过本文对各种方法的比较,我们发现列举、算术巧算到代数方法各种方法并不是独立不相关的,其实只是呈现表述方式不同,本质是一样的。正如莱布尼茨所说,是“换个方式来考虑的”。每种做法都是一种创新,创新人才的培养,应该是核心素养研究和培养的根本目的。
参考文献:
[1]《数学》四年级下(人民教育出版社).
[2]《数学》七年级上(人民教育出版社).
[3]《数学与生活》( 日本)远山启 (人民邮电出版社).
[4]《数学课程标准》(北京师范大学出版社).
作者简介:和文涛(1969-2),男,中央民族大学毕业,云南大学附属中学教师,高级教师,数学教研组长,2010年国培计划培训团队研修项目华师大初中数学班结业,云南省名师讲学团成员,曾荣获昆明市优秀园丁,一直从事初中数学教学研究。

