线性规划模型的教学研究及探讨*
刘奇飞 邓 华
湖南人文科技学院数学金融学院,湖南 娄底 417000
线性规划模型的教学研究及探讨*
刘奇飞 邓 华
湖南人文科技学院数学金融学院,湖南 娄底 417000
本文主要对线性规划模型进行教学研究并探讨。首先介绍了与线性规划问题相关的理论知识,举实例说明线性规划在最优分配中的重要性,再运用Lingo软件对其求解。
线性规划;最优分配;lingo软件
线性规划模型的标准型为:
目标函数maxZ=c1x1+c2x2+…+cnxn
(1)
(2)
其中约束条件是一组线性等式,称为约束方程组。目标函数为求最大化问题,约束条件为等式,所有变量非负。
线性规划在配料问题中的应用:随着畜牧业的发展,养殖规模的扩大,如何控制生产成本成为一个热点话题。在大规模的养殖生产中,怎样才能做到在满足动物成长需要的基础上,使成本降到最低,这就是线性规划中的配料问题。
设某公司饲养实验用的动物以供出售,已知这些动物的生长对饲料中3种营养(蛋白质、矿物质和维生素)特别敏感,每个动物每周至少需要蛋白质60g,矿物质3g,维生素8mg,该公司能买到5种不同的饲料,每种饲料1kg所含各种营养成分和成本如表所示,如果每个小动物每周食用饲料不超过52kg,怎样配料才能既满足动物生长需要,又使总成本最低。
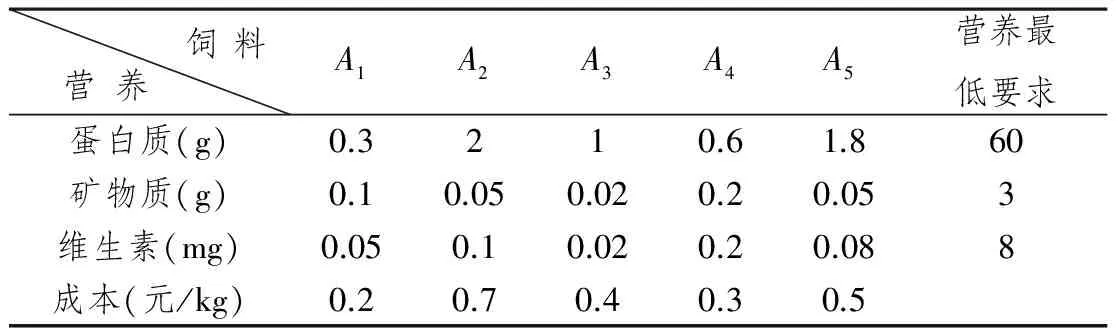
表1
设需要饲料A1,A2,A3,A4,A5分别为x1,x2,x3,x4,x5kg,
目标函数为:mins=0.2x1+0.7x2+0.4x3+0.3x4+0.5x5
每个动物每周需要的蛋白质不能少于60g,得到约束条件:
0.3x1+2x2+x3+0.6x4+1.8x5≥60
每个动物每周需要的矿物质不能少于3g,得到约束条件:
0.1x1+0.05x2+0.02x3+0.2x4+0.05x5≥3
每个动物每周需要的维生素不能少于8g,得到约束条件:
0.05x1+0.1x2+0.02x3+0.2x4+0.08x5≥8
建立线性规划模型:
mins=0.2x1+0.7x2+0.4x3+0.3x4+0.5x5
运用lingo软件对其求解,如下图:
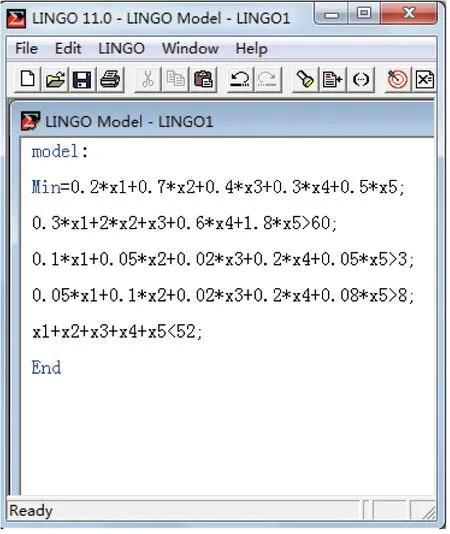
运行结果得当每周每个动物的配料饲料A2、A4、A5分别为12kg、30kg和10kg时,可使得饲养成本达到最低,最低成本为22.4元;不选用饲料A1和A3的原因是因为这两种饲料的价格太高了,没有竞争力。
在建立线性规划模型时,主要分三个部分,先选择决策变量,再建立目标函数及约束条件。这三者称为线性规划的三要素,其中最关键的为决策变量。决策变量的选取并不是唯一的,但决策变量选取是否恰当,直接影响到线性规划模型的难易程度。
[1]谢金星,薛毅.优化建模与LINDO/LINGO软件[M].北京:清华大学出版社,2005.
[2]魏权龄,胡显佑.运筹学基础教程[M].中国人民大学出版社,2008.
*主持校级教改项目“转型形势下地方高校金融工程专业应用技术型人才培养模式研究”(RKJGY1627)。
G
A
1006-0049-(2017)11-0069-01

