海上风电并网的有限控制集模型预测控制

许加柱， 袁晋蓉， 沈阳武， 邓小亮， 熊尚峰， 吴和海

(1．湖南大学 电气与信息工程学院，湖南 长沙 410082；2．湖南省电力公司电力科学研究院，湖南 长沙 410007；3.湖南省电力公司，湖南 长沙 410007)

海上风电并网的有限控制集模型预测控制

许加柱1， 袁晋蓉1， 沈阳武2， 邓小亮3， 熊尚峰2， 吴和海1

(1．湖南大学 电气与信息工程学院，湖南 长沙 410082；2．湖南省电力公司电力科学研究院，湖南 长沙 410007；3.湖南省电力公司，湖南 长沙 410007)

针对海上风电场柔性直流输电(voltage source converter high voltage direct current,VSC-HVDC)系统传统矢量控制中，PI参数难以整定、需要调制器以及难以实现多目标优化等问题，提出了一种基于有限控制集模型预测控制(finite control set model predictive control，FCS-MPC)的新型海上风电VSC-HVDC并网控制策略。该方法结合并网逆变器的离散数学模型，通过电流误差构造价值函数，以价值函数为优化目标，预测并网逆变器未来时刻的开关状态；为避免计算时间延时并实现多目标优化，引入延时补偿和权重系数，产生最优开关组合触发并网逆变器。在Matlab/SIMULINK中建立风电并网系统的仿真模型，并采用FCS-MPC和传统PI控制两种方法实施并网控制，通过对风电场功率波动及电网发生故障等多种运行环境进行仿真，结果有效验证了所提出的FCS-MPC方法应用于VSC-HVDC海上风电场并网系统对直流电压的控制能力和故障恢复能力。

海上风电场；并网逆变器；有限控制集模型预测控制；故障恢复

0 引 言

为了应对资源短缺和环境污染问题，发展风电等可再生能源得到世界各国的高度重视。海上风电由于具有风能利用效率高、不占用陆地土地资源等优势，已成为未来风电发展的重点[1]。随着海上风电装机容量的迅猛增长和电力电子变流技术的不断革新，电压源换流器高压直流输电(voltage source converter high voltage direct current,VSC-HVDC)技术在海上风电并网应用中得到学术界与工业界的广泛关注，并对海上风电场VSC-HVDC变流器运行性能提出了更高要求[2-3]。

模型预测控制[4-9](model predictive control， MPC)功能强大、控制灵活、不需要调制器、无需解耦、可包含约束条件并能进行在线优化处理等优点，在国内外得到迅速发展。MPC在模块化多电平换流器[10]、不间断电源[11]、中性点箝位变换器[12]等领域得到广泛应用。

文献[13]在上述基础上把MPC应用于光伏电站低电压穿越，提高了光伏电站的暂态稳定性。文献[14-15]通过有限控制集(finite control set，FCS)模型预测控制来优化变流器控制，对比传统控制算法，改善了逆变器输出电压质量。文献[16-17]针对STATCOM及五电平换流器提出了一种改进型模型预测控制策略，实现优化控制。文献[18-19]把模型预测控制用于降低交流电机控制复杂性研究，具有良好的控制性能。上述研究多针对模型预测控制的变流器稳态运行性能，涉及新能源并网及并网后外部扰动特别是系统故障下的运行性能还有待进一步评估。

本文针对上述研究的不足，结合FCS-MPC对海上风电并网特性进行研究，构建了一种基于柔性直流输电的风电并网侧FCS-MPC电流控制策略。该控制策略通过外环产生所需参考值，与给定电压矢量下的预测电流值比较，使得差值最小的价值函数所对应的开关状态于下一采样周期使用，实现对参考值的快速跟踪。并通过对延时补偿和权重系数的设计来增强系统的抗扰动能力及故障恢复能力。本文在Matlab/SIMULINK上设计了风电经VSC并网仿真模型，对比于传统的PI双闭环控制策略，在不同输入风电功率及电网直流故障、网侧交流故障及电网电压跌落情况下分别验证FCS-MPC的优越性。

1 WF-VSC和PMSG风电场控制

图1给出了典型海上风电场通过双端柔性直流输电系统并网的拓扑结构。系统由风电场、VSC-HVDC输电系统和交流电网构成。VSC-HVDC输电系统包含风电场侧电压源型换流器(WF-VSC)、电网侧电压源型换流器(GS-VSC)和海底直流输电网络。为了保证海上风电场输出功率的并网消纳和VSC-HVDC输电系统的安全运行，需要维持VSC-HVDC输电系统的功率平衡，因此GS-VSC主要功能是维持控制直流传输网络直流电压稳定。

图1 海上风电场经柔性直流输电并网示意图Fig.1 Schematic diagram of offshore wind farm connected to the grid through VSC-HVDC

1.1 WF-VSC控制策略

风电场侧变流器WF-VSC的拓扑结构如图2所示。

风电场侧变流器WF-VSC在dq同步旋转坐标系下的数学模型为：

(1)

式中：usd、usq分别为三相电压的d、q轴分量；isd、isq分别为三相电流的d、q轴分量；vsd、vsq分别为变流器侧电压d、q轴分量；Ssd、Ssq分别为开关函数的d、q轴分量；ωs为电网同步旋转角速度。

图2 WF-VSC拓扑结构图Fig.2 Topology graph of WF-VSC

WF-VSC自动吸收风电场发出的风功率，因此，WF-VSC采用直接控制策略来维持风电场侧电网的电压幅值和频率恒定。WF-VSC控制框图如图3所示。

由图3可知，风电场电网电压幅值和相位通过设定WF-VSC控制系统的d轴、q轴指令和同步旋转角度指令来控制。为简化控制，风电场电压初始相角设置为0，仅引入交流系统d轴和q轴电压幅值进行反馈控制，风电场交流d轴和q轴电压幅值参考指令与实时d轴和q轴电压幅值的差值经过PI控制器后得到调制比M来产生相应的触发脉冲。

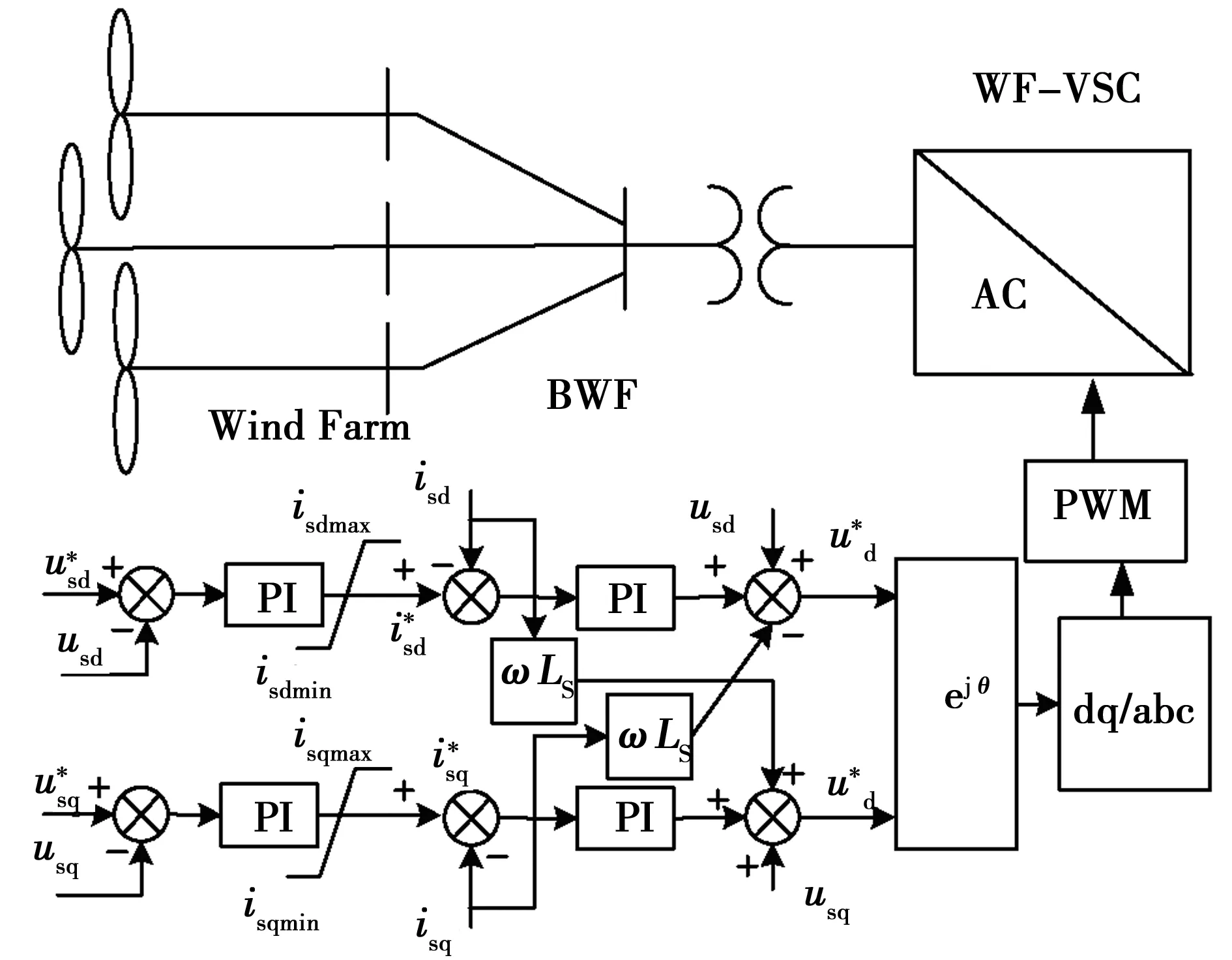
图3 WF-VSC控制策略Fig.3 WF-VSC control strategy

1.2 PMSG风电场控制策略

PMSG典型拓扑结构如图4所示。直驱永磁风力发电系统由风力机、永磁同步发电机、机侧换流器和网侧换流器构成。机侧换流器主要采用转速外环和电流内环的双闭环控制策略实现MPPT。网侧换流器通过控制直流电压的稳定实现风功率的并网，本文中PMSG风电场采用单机等值模型。由于网侧变流器的动态响应速度远远快于风力机和机侧换流器的动态响应速度，为便于分析，对PMSG进行简化处理，将风力机、永磁同步发电机和机侧换流器等效为一个直流电压源，如图4所示。风速变化引起的风功率变化通过控制网侧变流器输出功率来模拟。

图4 永磁直驱风力发电系统拓扑结构等效变换图Fig.4 Topology structure equivalent transformation diagram of permanent magnet direct drive wind power generation system

PMSG网侧变流器的控制策略如图5所示。本文主要验证在风速变化及电网发生各类故障情况下，所提出的控制策略能很好的抗扰动及具有良好的故障恢复能力，因此风电输入功率随着风速的变化可通过PMSG网侧变流器控制来实现。由图5可知，通过风电功率发生器来模拟实际风速，产生变化的输入功率，并得到三相交流参考电流值的d轴分量。三相交流电压参考值和测量模块测出的实际值进行比较，并通过PI环节得到三相交流参考电流值的q轴分量。d轴分量和q轴分量进行PI调节，再进行派克反变换，对变流器进行控制。

图5 PMSG网侧控制器PI控制图Fig.5 PI control diagram of PMSG network side controller

2 FCS-MPC的GS-VSC控制策略

2.1 GS-VSC的离散化预测模型

GS-VSC是风力发电系统与电网相连的接口，其控制性能是保证风电稳定并网的前提。变流器拓扑结构如图6所示，ua、ub、uc分别表示变流器输出电压；ia、ib、ic分别表示电网三相电流；ea、eb、ec分别表示电网三相电压；L、R和C分别为换流电抗器、等效电阻及直流电容;udc、idc、iL分别为直流电压、直流输入电流及直流输出电流。

为了获取电网电流预测模型，首先要对GS-VSC进行数学建模，三相静止坐标下电网电流的动态方程可以表示为

(2)

式中：i为电网电流矢量；u为变流器输出的电压矢量；e为电网电压矢量。

图6 GS-VSC拓扑结构图Fig.6 Topology graph of GS-VSC

电流电压空间矢量可定义为

(3)

式中：a=ej2π/3，uaN、ubN、ucN分别代表变流器的输出对中性点N的电压。

uaN、ubN、ucN可由开关函数Sx和直流电压的乘积获得

uxN=Sxudc,(x=a,b,c)。

(4)

开关函数Sx(x=a,b,c)反映GS-VSC每一相桥臂的开关状态，可定义为如下形式：

(5)

假设信号采样周期为Ts，则电网电流导数可通过前向欧拉逼近方法进行离散化，有

(6)

式中：i(k+1)和i(k)分别为第k+1周期和第k周期采样得到的电流值。

将式(6)代入式(2)，可以得到GS-VSC预测电流表达式。

(7)

通过克拉克(Clarke)变换，可得式(7)在αβ坐标系下的离散表达式为

(8)

式中：iα(k+1)和iβ(k+1)分别为αβ坐标系下电流在第k+1时刻的α轴分量和β轴分量；uα(k)、uβ(k)、eα(k)、eβ(k)分别为k时刻变流器出口电压的α轴分量和β轴分量及电网电压的α轴分量和β轴分量。

由式(8)可以看出，通过GS-VSC在k时刻的电压与电流采样值，可以准确地预知GS-VSC在k+1时刻的电流值。因此能够准确快速实现对GS-VSC电流的跟踪控制和增强GS-VSC对系统故障扰动的抵御能力。

2.2 基于FCS-MPC的GS-VSC基本控制原理

GS-VSC的首要控制目标是维持VSC-HVDC输电系统的功率平衡，实现风电场输出功率的并网消纳。其控制原理是根据输出目标参考指令和GS-VSC输入信息(运行状态信息)，确定GS-VSC各桥臂的开关函数值即桥臂的开关状态，进而控制GS-VSC的输出电压矢量(U)，U与电网电压矢量E共同作用于等效连接阻抗Zs，产生相位和幅值可控的三相电流ia、ib和ic，从而实现对GS-VSC输入、输出功率的准确控制。因此GS-VSC输出电压矢量U的确定是GS-VSC有电流(功率)控制的关键。

由式(4)和式(5)可知，GS-VSC交流侧输电电压矢量(U)由GS-VSC3个桥臂的开关函数(Sa、Sb和Sc)决定。本文中假设GS-VSC为三相两电平变流器结构，考虑到所有可能的有限个门控信号Sx(Sa、Sb和Sc)的组合，可获得8种开关状态和与之对应的电压矢量，由于U0=U7，在复平面只产生7个不同电压矢量的有限集合。表1给出了GS-VSC 3个桥臂的开关函数取不同值对应的GS-VSC输出电压值。

表1 价值函数、开关状态和电压矢量对应关系

传统的GS-VSC采用功率外环和电流内环的双闭环控制结构来确定GS-VSC 3个桥臂的开关函数(Sa、Sb和Sc)，控制GS-VSC的交流侧输出电压U，最终实现对GS-VSC电流(功率)的控制。然而传统PI调节器参数对系统模型参数比较敏感，PI参数整定困难。同时，传统控制策略需要对受电路参数影响的前馈补偿项进行解耦控制，且难以实现对目标的优化控制。为了克服传统控制策略的不足，本文提出了一种基于有限控制集模型预测控制(FCS-MPC)的海上风电场VSC-HVDC并网控制策略。

FCS-MPC是一种基于模型的闭环优化控制方法。根据变流器输出的8种有限数量的开关状态组合(Sa、Sb和Sc)以及所对应的电压矢量U，通过式(8)所示的GS-VSC离散数学预测模型，得到下一时刻GS-VSC电流的所有可能预测值。参考值和各个电流预测值通过式(9)所示的价值函数进行比较，选择使价值函数最小的电压矢量所对应的开关组合作为GS-VSC触发脉冲信号，实现对GS-VSC输出电流的最优控制。

(9)

式中igα、igβ分别是对于给定电压矢量下预测电网电流矢量的实部和虚部。

在下一个采样周期内重复上述过程，如此循环往复，在整个运行过程中对GS-VSC的输出电流进行滚动优化控制。图7给出了GS-VSC的模型预测控制框图。

图7 GS-VSC控制策略Fig.7 GS-VSC control strategy

由上述分析可知，相比于传统基于PI调节器的双闭环控制，FCS-MPC通过有限的开关状态直接控制变流器，减少繁琐的PI整定，无需解耦，不用进行多次变换，无需复杂的PWM调制器，可包含多重约束条件并进行优化处理，复杂性低且在开关状态个数为8的两电平换流器中计算量最小。

2.3 计及时延的GS-VSC的FCS-MPC控制设计

式(9)构造了以参考电流和预测电流的误差函数为目标的价值函数，即将求取满足控制目标的最优调制波的问题转化为求取使价值函数最小的最优开关组合。然而，式(9)所示的价值函数中的电流参考值为未来值，将会引起FCS-MPC控制策略的延时，影响FCS-MPC的控制精确性和响应速度。为了防止延时问题使系统性能恶化，需要对计算时间延时进行补偿。本文提出通过tk+2时刻的预测电流值来修改价值函数，tk+2时刻的预测电流函数为

(10)

考虑延时补偿后的价值函数为

igβ(k+2)|。

(11)

式(11)进行延时补偿后的价值函数具有较好的灵活性，对于系统其他所需要的约束条件可以方便地添加在价值函数中进行处理。

为了在风电场功率波动及故障情况下能保持直流电压的稳定,将直流电压误差添加到式(11)中构造新的价值函数为

(12)

其中λ为权重系数。价值函数中加入直流电压预测，提高稳态和故障过程中直流电压的稳定性。

图8 模型预测电流控制流程图Fig.8 Flow chart of model predictive current control

GS-VSC 的模型预测控制算法流程图如图8所示，具体的控制步骤可以概括为：

1)通过对8个开关状态及其与输入/输出的电压及电流之间的关系，建立GS-VSC的数学模型；

2)建立离散时间模型用以预测要控制的变量的未来行为；

3)在所应用开关状态的基础上，建立用于预测的tk+1时刻电流模型；

4)预测在所适用的开关状态下的tk+2时刻电流；

5)定义一个可代表期望的系统行为的价值函数g；

6)选择使价值函数g最小所对应的电压矢量，同时产生相应的开关状态信号；

7)更新开关状态，返回到步骤2)，循环到下一采样周期。

3 仿真分析

为了验证本文所提出的FCS-MPC的有效性，在Matlab/SIMULINK中建立如图1所示的海上风电集群(由4个300 MW的风电场组成)柔性并网模型，仿真参数如表2所示。

表2 系统仿真参数Table 2 Simulation parameters of system

3.1 算例1：风电场功率波动

本算例对采用FCS-MPC控制策略和传统PI双闭环控制策略的海上风电柔性直流输电系统在风功率波动下的运行性能进行了仿真对比分析。风电场输出功率0～1 s为600 MW；1s后功率逐渐上升， 100 ms后输出功率达到1 100 MW；1.1 s后风电场输出功率维持在1 100 MW。仿真运行期间风电场保持单位功率因数运行。采用不同控制策略的海上风电柔性直流输电系统的仿真结果如图9所示。

由图9可知，在风速(风电场输出功率)变化时，采用本文所提出的FCS-MPC控制策略和传统双闭环PI控制策略，GS-VSC均能够快速响应风电场输出功率的动态变化，实现风功率的平稳快速并网。相对于传统双闭环PI控制策略，FCS-MPC采用单电压外环控制策略，因此GS-VSC的并网有功功率(见图9(a))、和并网电流(见图9(b))对相应参考指令具有更快的响应速度和准确性。同时，由图9(c)可见，由于FCS-MPC控制策略的价值函数中引入了直流电压预测控制，采用FCS-MPC控制策略后VSC-HVDC输电系统的直流电压在风电场输出功率动态变化时能够快速地恢复到参考值，具有更好的动态稳定性。因此，本文所提出的FCS-MPC不仅能够实现海上风电场VSC-HVDC输电系统的稳定运行，而且比传统双闭环PI控制策略具有更好的稳态性能。

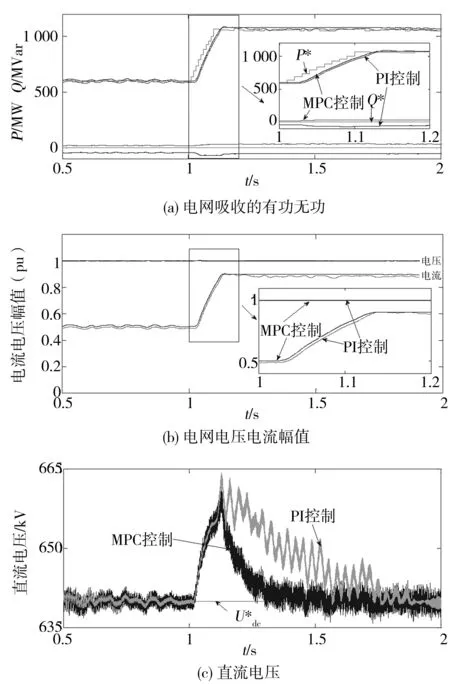
图9 FCS-MPC和PI控制在风电场功率波动下响应特性图Fig.9 Response characteristic of FCS-MPC and PI control under wind farm power fluctuation

3.2 算例2：网侧交流故障

2.0 s电网侧发生三相短路接地故障，故障持续时间10 ms后切除，海上风电场VSC-HVDC输电系统的响应特性如图10所示。

由图10可以看出，采用传统双闭环PI控制策略，GS-VSC输出有功功率、无功功率、交流侧输出电压和电流受电网故障影响较大，故障切除后都经过较长时间波动才逐渐恢复平稳，同时由于传统双闭环PI控制策略的直流电压控制能力受限，3 s内直流电压无法恢复到其故障前水平。采用本文所提出的FCS-MPC策略，有功功率、无功功率仅有小波动，随即平稳；电压能在故障后快速恢复，电流影响很小；直流电压能够在2.5 s达到稳定，这是因为FCS-MPC中引入直流电压预测控制，能够有效提高GS-VSC在故障期间对直流电压的控制能力。

3.3 算例3：直流故障

2.0 s时直流侧线路左侧发生持续时间为100 ms的直流线路接地故障，VSC-HVDC输电系统采用不同控制策略的运行特性如图11所示。

图10 FCS-MPC和PI控制在网侧交流故障下响应特性图Fig.10 Response characteristic of FCS-MPC and PI control under AC fault of grid side

由图11易知，采用PI双闭环策略时，故障期间有功功率跌落到-2 200 MW，无功功率跌落到-2 000 Mvar，经过0.2 s有功功率和无功功率都恢复到正常值(见图11(a))；交流电压幅值从1 pu跌落到0.75 pu(见图11(b))，交流电压跌落幅度达到0.25 pu；并网电流最的最大暂态峰值到达5 pu(见图11(c))，远远超过GS-VSC的最大暂态峰值电流承受水平。

采用FCS-MPC策略，直流短路故障时，有功功率和无功功率分别从1 060 MW跌落到-1 000 MW和0跌落到-1 000 Mvar(见图11(a))，远远小于采用传统双闭环PI控制策略的跌落程度；交流电压幅值从1 pu跌落到0.9pu(见图11(d))，跌落幅度仅为0.1 pu；故障期间交流电流的最大暂态峰值比传统双闭环控制策减少2.4 pu，仅为2.6 pu(见图11(e))。由此可见，FCS-MPC在直流短路故障时交流电压电流以及有功无功的波动均小于PI双闭环控制,电流电压波形质量较高。

图11 PI和FCS-MPC控制在直流故障下响应特性图Fig.11 Response characteristic of PI and FCS-MPC control under DC fault

3.4 算例4：电网电压跌落

为进一步验证FCS-MPC控制策略的有效性，对电网电压发生跌落时海上风电VSC-HVDC输电系统的动态性能进行仿真验证。2.0 s时系统侧故障导致电网电压幅值跌落至额定电压的一半，即0.5 pu，持续时间为100 ms。仿真结果如图12所示。

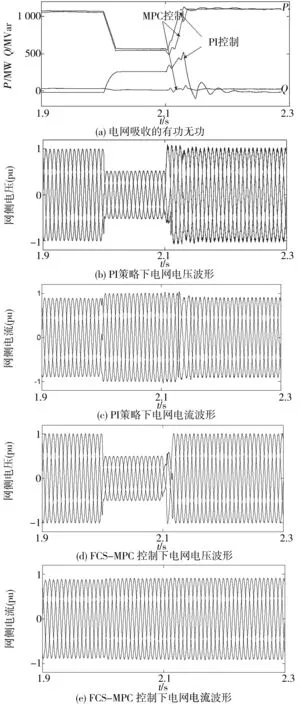
图12 PI和FCS-MPC控制在电网电压跌落下响应特性图Fig.12 Response characteristic of PI and FCS-MPC control under grid voltage sag

由图12可以看出，当发生电网电压跌落故障时，采用FCS-MPC控制策略，有功功率从1 060 MW跌落到540 MW，在2.14 s恢复到故障前水平，无功功率仅有小波动；故障切除后交流电压能够快速恢复到1 pu，交流电流基本无变化。采用PI双闭环策略，有功功率从1 060 MW跌落到550 MW，故障切除后0.15 s恢复到故障前水平，无功功率Q上升到500 MVar，经过0.25 s才恢复正常；交流电压和交流电流经过较长时间才恢复到故障前的稳定值。综合可见，采用FCS-MPC策略在交流电压故障时交流电流及无功的影响小与PI双闭环策略，具有更强的抗干扰能力。

3.5 谐波畸变率对比分析

选取风电场最大输出功率(算例1)的1.2～1.4 s时间段及各种故障(算例2～算例4)切除后的2.3～2.5 s内稳定时间段进行傅里叶分析，各种运行工况后交流电压电流的总谐波畸变率如图13所示。

图13 谐波畸变率对比Fig.13 Comparison of harmonic distortion

图13中，Ⅰ区代表风功率波动后的稳态运行工况傅里叶分析结果、Ⅱ区代表网侧交流故障傅里叶分析结果、Ⅲ区代表直流故障傅里叶分析结果，Ⅳ区代表电网电压跌落傅里叶分析结果。由图13可知，采用FCS-MPC控制策略，GS-VSC并网电压和电流的谐波畸变率不超过1%，远远低于传统双闭环PI控制策略的谐波畸变率。

4 结 论

针对海上风电场VSC-HVDC变流器运行性能问题，本文提出了基于FCS-MPC的新型并网控制策略。所提出的FCS-MPC控制策略结构简单，省略了电流内环，减少了PI参数难以整定的繁琐调制过程，并可实现对海上风电VSC-HVDC输电系统的多目标优化。同时，所提出的控制策略考虑了控制时延影响，并通过在FCS-MPC价值函数中引入直流电压预测项提高对VSC-HVDC输电系统直流电压的控制稳定性，增加VSC-HVDC输电系统抗扰动性能及故障恢复能力。对FCS-MPC控制策略在风电场功率波动、电网三相接地、直流短路故障及电网电压跌落情况下的运行性能进行了仿真分析。仿真结果表明，FCS-MPC控制策略具有良好的动态性能和模型参数鲁棒性，能够显著提高海上风电VSC-HVDC输电系统的抗扰动性能及故障恢复能力，降低系统并网电压与电流的谐波畸变率。

[1] 江道灼,谷泓杰,尹瑞,等.海上直流风电场研究现状及发展前景[J].电网技术,2015,39(9):2424-2431. JIANG Daozhuo,GU Hongjie,YIN Rui,et al.Research status and developing prospect of offshore wind farm with pure DC systems[J].Power System Technology,2015,39(9):2424-2431.

[2] 师楠,朱显辉.风电并网的频率控制问题[J].哈尔滨理工大学学报,2012,17(2):84-88. SHI Nan,ZHU Xianhui.The frequency control issues about wind farm grid integration[J].Journal of Harbin University of Science and Technology,2012,17(2):84-88.

[3] 王志新,吴杰,徐烈,等.大型海上风电场并网VSC-HVDC变流器关键技术[J].中国电机工程学报,2013(19):14-26. WANG Zhixin,WU Jie,XU Lie,et al.Key technologies of large offshore wide farm VSC-HVDC convertersfor grid integration[J].Proceedings of the CSEE,2013(19):14-26.

[4] 梁营玉,张涛,刘建政,等.向无源网络供电的VSC-HVDC模型预测控制[J].电工技术学报,2015,30(11):78-89. LIANG Yingyu,ZHANG Tao,LIU Jianzheng,et al.Model predictive control for VSC-HVDC supplying passive networks[J].Transactions of China Electrotechnical Society,2015,30(11):78-89.

[5] RODRIGUEZ J,CORTES P.Predictive control of power converters and electrical drives[J].Predictive Control of Power Converters & Electrical Drives,2012,6(4):1785 - 1786.

[6] CORTES P,RODRIGUEZ J,SILVA C,et al.Delay compensation in model predictive current control of a Three-Phase inverter[J].IEEE Transactions on Industrial Electronics,2012,59(2):1323-1325.

[7] KOURO S,CORTES P,VARGAS R,et al.Model predictive control—a simple and powerful method to control power converters[J].IEEE Transactions on Industrial Electronics,2009,56(6):1826-1838.

[8] WILSON A,KOURO S,RODRIGUEZ J,et al.Model predictive control of multilevel cascaded H-Bridge inverters[J].IEEE Transactions on Industrial Electronics,2010,57(8):2691-2699.

[9] 王萌,施艳艳,沈明辉.三相电压型PWM整流器定频模型预测控制[J].电机与控制学报,2014,3:46-53. WANG Meng,SHI Yanyan,SHEN Minghui.Model predictive control with fixed switching frequency for three-phase voltage source PWM rectifier[J].Electric Machines and Control,2014,3:46-53.

[10] RIVERA S,KOURO S,WU B,et al.Multilevel direct power control—a generalized approach for Grid-Tied multilevel converter applications[J].IEEE Transactions on Power Electronics,2014,29(10):5592-5604.

[11] CORTES P,ORTIZ G,YUZ J I,et al.Model predictive control of an inverter with output LC filter for UPS applications[J].IEEE Transactions on Industrial Electronics,2009,56(6):1875-1883.

[12] CALLE-PRADO A,ALEPUZ S,BORDONAU J,et al.Model predictive current control of Grid-Connected Neutral-Point-Clamped converters to meet Low-Voltage Ride-Through requirements[J].IEEE Transactions on Industrial Electronics,2015,62(3):1503-1514.

[13] 贾利虎,朱永强,孙小燕,等.基于模型电流预测控制的光伏电站低电压穿越控制方法[J].电力系统自动化,2015,7:68-74. JIA Lihu,ZHU Yongqiang,SUN Xiaoyan,et al.A control method of low voltage ride through for photovoltaic plant based on model current predictive control[J].Automation of Electric Power Systems,2015,7:68-74.

[14] 李宁,李颖晖,韩建定,等.基于混合逻辑动态模型的三相逆变电路有限控制集模型预测控制策略[J].电网技术,2014,38(2):375-380. LI Ning,LI Yinghui,HAN Jianding,et al.FCS-MPC strategy for inverters based on MLD model[J].Power System Technology,2014,38(2):375-380.

[15] 沈坤,章兢,王坚.一种多步预测的变流器有限控制集模型预测控制算法[J].中国电机工程学报,2013,32(33):37-44. SHEN Kun,ZHANG Jing,WANG Jian.A model predictive control scheme of Multi-step prediction finite control set for converters[J].Proceeding of the CSEE,2013,32(33):37-44.

[16] 杨兴武,徐亚军,薛花.基于FS-MPC的级联型STATCOM控制延时消除方法[J].电机与控制学报,2014,18(11):84-89. YANG Xingwu,XU Yajun,XUE Hua.Control delay elimination for cascaded multilevel STATCOM based on finite states model predictive control[J].Electric Machines and Control,2014,18(11):84-89.

[17] 朱玲,符晓巍,胡晓波,等.模块化多电平变流器HVDC系统的模型预测控制[J].电力系统保护与控制,2014(16):1-8. ZHU Ling,FU Xiaowei,HU Xiaobo,et al.Model predictive control of modular multilevel converter for HVDC system[J].Power System Protection and Control,2014(16):1-8.

[18] 王永宾,林辉,计宏.多约束永磁同步电机稳定模型预测控制策略[J].电机与控制学报,2011,15(12):7-13. WANG Yongbin,LIN Hui,JI Hong.Stabilizing model predictive controlstrategy for permanent magnet synchronous motor with multi-variable constraints[J].Electric Machines and Control,2011,15(12):7-13.

[19] 何凤有,王从刚,曹晓冬,等.感应电机准无差拍模型预测电流控制策略[J].电机与控制学报,2013,17(9):57-62. HE Fengyou,WANG Conggang,CAO Xiaodong,et al.Quasi-deadbeat model predictive current control strategy for induction motor drives[J].Electric Machines and Control,2013,17(9):57-62.

Finite-control-set model predictive control for offshore wind power integration

XU Jia-zhu1， YUAN Jin-rong1， SHEN Yang-wu2， DENG Xiao-liang3， XIONG Shang-feng2， WU He-hai1

(1.College of Electrical and Information Engineering,Hunan University,Changsha 410082,China; 2.Hunan Electric Power Corporation Research Institute,Changsha 410007,China; 3.Hunan Electric Power Corporation,Changsha 410007,China)

To overcome the problems such as PI parameters tuning,modulator requirement and multi-objective optimization in traditional vector control strategy,a FCS-MPC strategy of grid-connected inverters for offshore wind farm VSC-HVDC was proposed.Based on the discrete mathematical model of grid-connected inverters,this strategy can predict the switching states of grid-connected inverters in future moments by considering the current error based value function as optimization objective.To avoid the computing time delay and to achieve multi-objective optimization,delay compensation and weighting coefficients were introduced to generate optimal switch combinations to drive the inverters.Simulation models using FCS-MPC and traditional PI controller respectively for wind power integration were established in MATLAB/Simulink.By means of simulations under various situations such as wind power fluctuations,grid fault occurrences,etc,it validates the desirable performances of the offshore wind farm VSC-HVDC with the proposed FCS-MPC in DC voltage control and fault recovery.

offshore wind farm; grid-connected inverter; finite control set model predictive control; fault recovery

2016-02-15

国家自然科学基金(51477044)

许加柱(1980—)，男，博士，教授，博士生导师，研究方向为交直流电能变换理论与新技术及电气化铁路电能质量治理； 袁晋蓉(1992—)，女，硕士研究生，研究方向为新能源及柔性直流输电技术； 沈阳武(1985—)，男，博士，研究方向为电力系统规划、新能源与储能技术及其在电力系统中的应用； 邓小亮(1986—)，男，硕士，研究方向为新能源管理和并网分析； 熊尚峰(1980—)，男，硕士，研究方向为电力系统自动化； 吴和海(1992—)，男，硕士研究生，研究方向为电力系统经济调度。

袁晋蓉

10.15938/j.emc.2017.05.004

TM 464

A

1007-449X(2017)05-0023-10