LMS滤波法在笼型异步电机转子断条诊断中的特征

刘新正， 何升华， 高琳， 张厚成

(1.西安交通大学 电气工程学院，陕西 西安 710049；2.南京深科博业电气股份有限公司，江苏 南京 211102)

LMS滤波法在笼型异步电机转子断条诊断中的特征

刘新正1， 何升华1， 高琳1， 张厚成2

(1.西安交通大学 电气工程学院，陕西 西安 710049；2.南京深科博业电气股份有限公司，江苏 南京 211102)

在诊断笼型异步电机转子断条故障时，可以通过对定子电流的频谱分析来提取代表故障特征的边频分量。为克服实际诊断中直接做快速傅里叶变换(fast fourier transformation,FFT)频谱分析存在的边频分量被主频量掩盖的缺陷，采用最小均方误差(least mean square,LMS)自适应滤波法滤除主频量再做FFT频谱分析，以突出边频分量。给出了转子断条故障诊断中LMS滤波原理及滤波器参数确定，详细分析了电机不同运行转差率下LMS滤波对边频量的采样规律和等效采样周期。结果表明，当依主频设定的固定采样周期采样电机电流时，LMS滤波是通过对边频分量在不同周波的不同位置采样拟合出完整周波，等效采样周期随转差率变化，且一般至少比设定的固定采样周期小一个数量级。

笼型异步电机；转子断条；频谱分析；最小均方误差；自适应滤波

0 引 言

鼠笼型异步电机转子出现断条后，其定子电流与正常相比会有一些变化，出现一些有别于供电主频率f1的附加频率分量[1-2]，例如频率为(1-2s)f1的左边频分量和频率为(1+2s)f1的右边频分量，其中s为转差率。

目前，转子断条故障的在线或者离线诊断所采用的大多数方法，是通过对定子电流的FFT频谱分析来提取故障特征[3-4]。对转差率较小的电机运行状态，边频分量幅值很小且频率离主频很近，极易被主频分量所掩盖。文献5采用最小均方误差(least mean square，LMS)自适应滤波法滤除定子电流中f1频率分量，在频谱图上突出断条诊断所需的(1-2s)f1和(1+2s)f1频率的特征分量。文献[6-8]采用起动电流的FFT频谱分析诊断转子断条。文献[9]将连续细化傅里叶变换、自适应滤波等技术相结合,可以在电机本身具有非对称及气隙偏心等因素情况下，实现高灵敏度、高可靠性的转子断条故障检测。但是，定子电流信号FFT频谱分析需要连续采样足够时长的定子电流信号，要求定子电流信号必须在足够时长内保持平稳，而电机实际运行中这一要求很难满足[9-11]。文献[10]将高频率分辨力谱估计的多重信号分类和旋转不变信号参数估计技术与模拟退火优化算法结合。文献[11]采用改进Prony方法，都希望在保证高频率分辨力的前提下，用尽可能短的定子电流信号采样时长实施转子故障检测。

在所有的自适应滤波技术中，LMS自适应滤波是一种简单有效且常用的方法[12-13]。本文将LMS自适应滤波算法应用于笼型异步电机转子断条故障诊断，先滤除主频量再做FFT频谱分析，以突出边频分量。详细分析了LMS滤波法对边频分量的采样规律，提出了等效采样周期的概念，归纳了其具有的特征和适用性。

1 转子断条诊断的LMS自适应滤波算法

自适应滤波原理框图[5]如图1所示。图中：is含待提取的信号ST和噪声nT；us为另外一个人为添加的信号，取其与噪声nT同频率；yT为自适应滤波器的输出。如果自适应滤波器的输出yT与噪声nT的大小相等、相位相反，就可以完全抵消噪声nT，合成信号eT中就不含有噪声nT。

图1 自适应滤波原理框图Fig.1 Diagram of adaptive filter algorithm

LMS自适应滤波是根据噪声nT的动态变化，自动调整滤波器的参数，获得与噪声nT相匹配的信号yT，以适应不同大小和相位的噪声信号，使eT在最小均方误差下逼近待提取信号ST。

为实现自适应滤波，需要ST与nT不相关，us与ST不相关而与nT相关。在转子断条故障诊断中，is为定子电流，其中含待提取的频率为(1-2s)f1和(1+2s)f1的信号ST和频率为f1的噪声信号nT；us选为定子电压信号，与噪声nT频率相同。可以证明，在一定条件下满足这2个条件，问题的关键就归结到滤波器参数的确定。

定义Tx为ST与nT互相关函数的积分上限[5]，并且令：

Tx·f1=K1，

(1)

Tx·f1(1-2s)=K2。

(2)

式(1)与式(2)之比为

(3)

将1/(1-2s)化为最简分式，取K1为最简分式的分子，K2为最简分式的分母，从而可求得Tx的大小为

(4)

将us、is和yT离散化后的信号分别记为us(k)、is(k)和yT(k)，则：

yT(k)=Aus(k)+Bus(k-1)。

(5)

式中A、B为滤波器的参数，由LMS自适应算法来确定。

误差信号e离散化后，按照最小均方误差条件，可得：

(6)

式中m为采样点数，其等于Tx和采样周期Ts之比且取整，即

(7)

式中：⎣」表示向下取整；Ts为采样周期，对50Hz工频电源供电下的电机，当进行转子断条故障诊断时，取Ts=0.005 s固定值。

将式(5)代入式(6)，并对A、B求偏导数再令其等于零，整理后得：

(8)

(9)

由于定子电压是频率为50 Hz的工频主频信号，当采样周期Ts=0.005 s时，意味着在一个工频周期中有4个采样点，根据电压信号正、负半周的对称性，有：

(10)

从而根据式(8)和式(9)，可以求得滤波器参数A、B分别为：

(11)

(12)

2 转子断条诊断中LMS滤波法的特征分析

在确定LMS滤波器参数时，用到了电压信号正、负半周的对称性，只有在1个主频周期有4个采样点时，才能使式(10)成立。所以，LMS滤波时采样周期Ts并不是越小越好，这是LMS滤波的1个特征。进一步分析可清楚地看出其他特征。

式(1)与式(2)的比值也可表示为

(13)

式(13)为主频信号频率f1与边频信号频率(1-2s)f1之比，即f1频率的主频信号单位时间周波数与(1-2s)f1频率的边频信号单位时间周波数之比。将式(13)改写为

(14)

式(14)为(1-2s)f1频率的边频信号周期与f1频率的主频信号周期之比，也意味着在相等的时间间隔内，(1-2s)f1频率的边频信号会出现K2个完整周波，而f1频率的主频信号会出现K1个完整周波。

式(4)取Tx=K1/f1，是表示在K1·1/f1时间内做采样，其总采样点数是根据式(7)计算得到的m=[Tx/Ts]，通常是一个较大的值。

依前所述，当进行转子断条故障诊断时，采样周期取固定值Ts=0.005 s。

对频率为50Hz的工频主频信号，一个周波中有4个采样点，不同周波总是在相同位置采样，m个总采样点数是在K1个周期做重复采样获得，这在一定程度上可以削弱单周波采样带来的随机干扰。

对频率为(1-2s)f1的边频信号，m个总采样点数是在K2个周波采样获得，是否会出现不同周波的重复采样，每个周波中有多少采样点，又与m和K2有关，会有以下3种情况。

1)m能够被K2整除。

如果m能够被K2整除，将其商记为m1，则m1为边频信号一个周波的采样点数，不同周期也是在相同位置采样，m个总采样点数是在K2个周期做重复采样获得。将此时对边频信号的等效采样周期用Tseq表示，则：

(15)

例如，f1=50 Hz，假设s=0.1，则边频信号频率f2=(1-2s)f1=40 Hz，根据式(3)且化为最简分式求得K1=5和K2=4。按照50Hz工频主频信号固定值Ts=0.005 s的采样周期，求得m=20，表示在主频信号的K1=5个周期和边频信号的K2=4个周期，都有m=20个采样点，如图2所示。图中，im和ib分别代表频率f1的主频信号和频率f2的边频信号，为讨论采样规律，幅值分别取1 A和0.5 A，并用“*”和“+”分别表示各自的采样点。图3和图4与此类似。因为m能够被K2整除，其商m1=5，在边频信号的一个周波仅有5个采样点，20个总采样点数是在4个周期做重复采样获得的，且等效采样周期Tseq=Ts。

此时，似乎只需要在边频信号的一个周期做采样即可，但这样做会使主频信号不是在完整周期采样，就违背了使式(10)成立的条件。因而，从LMS自适应滤波算法的整体考虑，必须做重复采样。同时，也像对主频信号的重复采样一样，附带的一个好处是削弱了单周期采样带来的随机干扰。

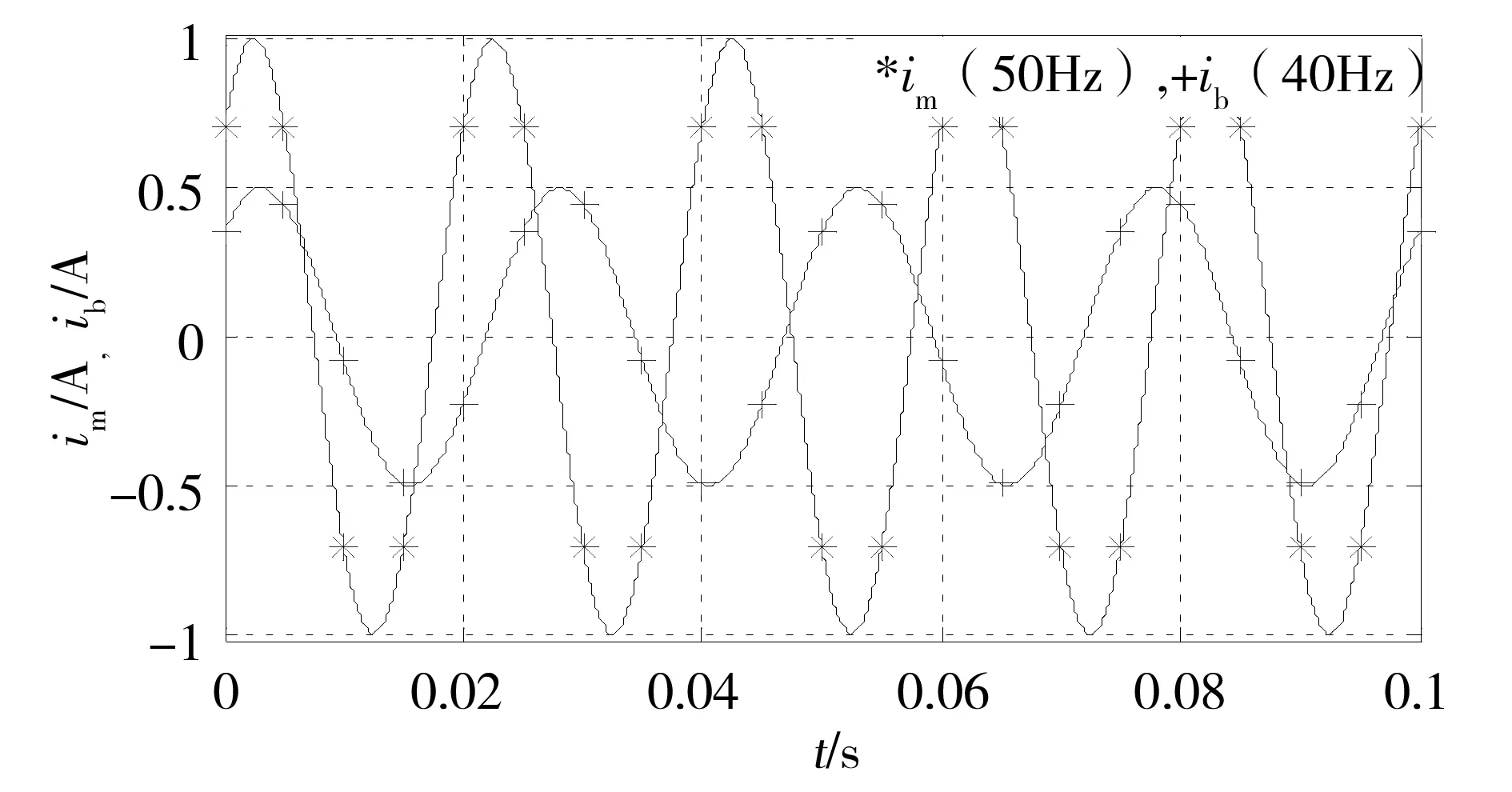
图2 s=0.1时主频和边频分量的采样特征Fig.2 Simpling features for main and side frequency component at s=0.1

2)m不能被K2整除但有大于1的最大公约数。

如果m不能被K2整除但有大于1的最大公约数，将最大公约数记为n1，将m除以n1所得的商(即m/K2最简分式的分子)记为m1，将K2除以n1所得的商(即m/K2最简分式的分母)记为K3，则n1为对边频信号做重复采样的循环次数，m1为一个循环中的采样点数，K3为一个循环中所包含的边频信号周波数。边频信号在K3个不同周期的不同位置采样，获得m1个采样点，恰好构成边频信号1个完整周波的采样。此时，边频信号的等效采样周期Tseq为

(16)

例如，f1=50 Hz，假设s=0.02，则边频信号频率f2=(1-2s)f1=48 Hz，根据式(3)且化为最简分式求得K1=25和K2=24。按照50Hz工频主频信号固定值Ts=0.005 s的采样周期，求得m=100，表示在主频信号的K1=25个周期和边频信号的K2=24个周期，都是有m=100个采样点，如图3所示。此时m不能被K2整除但有最大公约数n1=4，且有m1=m/n1=25和K3=K2/n1=6，表示对边频信号做4次循环采样，一个循环中有25个采样点，一个循环中包含有6个周波的边频信号。边频信号在6个不同周波的不同位置采样，获得25个采样点，恰好构成边频信号1个完整周期的采样，等效采样周期为

这一等效采样周期比工频信号的0.005s采样周期小1个数量级，提高了对边频信号的分辨率。

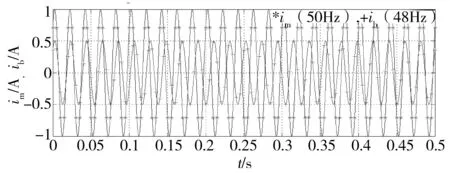
图3 s=0.02时主频和边频分量的采样特征Fig.3 Simpling features for main and side frequency components at s=0.02

3)m与K2互为质数。

如果m与K2互为质数，说明m既不能被K2整除又与K2没有大于1的最大公约数。此时，边频信号在K2个不同周期的不同位置采样，获得m个采样点，恰好构成边频信号1个完整周期的采样。

上述特征也可以理解为，在频率为(1-2s)f1的边频信号1个周期中，有1/[(1-2s)f1Ts]=4/(1-2s)个采样点，考虑到电机作电动运行时转差率s的实际变化范围，这一采样点数绝大多数情况下不是整数，而正是这一偏移量的存在，实现了对此边频信号在不同周期的不同位置采样。对应于边频信号的K2个周期，恰好形成了1个完整周期内的等间隔采样，m可以看成是在边频信号1个周期中的总采样点数。此时，边频信号的等效采样周期Tseq为

(17)

例如，f1=50 Hz，假设s=0.04，则边频信号频率f2=(1-2s)f1=46 Hz，根据式(3)且化为最简分式求得K1=25和K2=23。按照50Hz工频主频信号Ts=0.005 s固定采样周期，求得m=100，表示在主频信号的K1=25个周期和边频信号的K2=23个周期，都是有m=100个采样点，如图4所示。此时m不能被K2整除也没有最大公约数，边频信号在23个不同周期的不同位置采样，获得100个采样点，恰好构成边频信号1个完整周波的采样，等效采样周期为

这一等效采样周期更加小于对工频信号的Ts=0.005 s采样周期，可以大大提高对边频信号的分辨率。但是，这种等效采样，是用不同周波中的数据拟合出1个完整周期，仅适用于电机的稳态运行。

按照50Hz工频主频信号固定值Ts=0.005 s的采样周期，对电动机运行的一些特殊工况做具体分析，可以得到其他不同转差率下的采样规律如表1所示。可以看出，对电动机通常的满载运行转差率(2%～5%)，绝大多数情况下的等效采样周期都会大大减小。

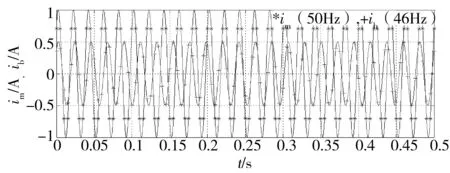
图4 s=0.04时主频和边频分量的采样特征Fig.4 Simpling features for main and side frequency components at s=0.04

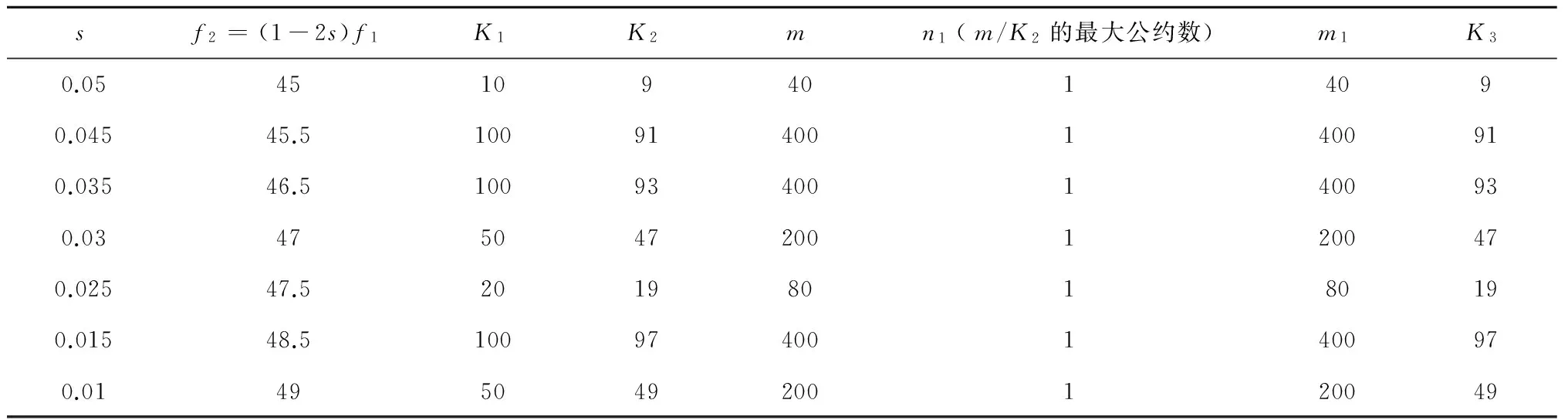
sf2=(1-2s)f1K1K2mn1(m/K2的最大公约数)m1K30.05451094014090.04545.5100914001400910.03546.5100934001400930.034750472001200470.02547.5201980180190.01548.5100974001400970.01495049200120049

3 转子断条诊断LMS滤波法的应用

用1个模拟转子断条的三相笼型异步电动机定子电流信号分析来验证自适应滤波方法的有效性。实验所用YGM112M-4型异步电机，4 kW，380 V，50 Hz，在转子导条上钻孔以模拟断条。实验装置及断条转子如图5所示，实验系统示意图如图6所示。

图5 实验装置及断条转子Fig.5 Experimental equipments and broken bar rotor

给异步电机施加220 V工频电压降额运行，经数据采集板采集电压、电流以及转速信号，送入上位计算机处理。绘出定子相电流波形如图7所示。此时，转速1 386 r/min，转差率s=0.076。

图6 实验系统示意图Fig.6 Diagram of experimental system

对定子电流直接做FFT频谱分析，得到图8所示频谱图。图中明显反映出了50Hz基波频率分量，但无法观察到(1-2s)f1和(1+2s)f1频率分量，这是由于(1-2s)f1和(1+2s)f1频率分量幅值过小，且非常靠近50Hz基波频率，从而被掩盖了。

对该定子电流先做LMS自适应滤波处理，求得K1=125、K2=106、Tx=2.5 s、m=500、n1=2、m1=250、K3=53，(1-2s)f1=42.4 Hz。此时的采样特征为：总采样时长2.5s；主频信号按每周波4个点，在125个周波的相同位置做重复采样，固定采样周期0.005s；边频信号在53个不同周波的不同位置共采样250点拟合出1个完整周波，重复采样两次，等效采样周期Tseq≈0.000 094 34 s。自适应滤波后再做FFT分析得到的定子电流频谱图如图9所示。

图7 定子相电流波形Fig.7 Waveform of stator phase current

图8 转子断条时定子电流的FFT分析频谱图Fig.8 FFT spectrum analysis result of stator current as rotor bar broken

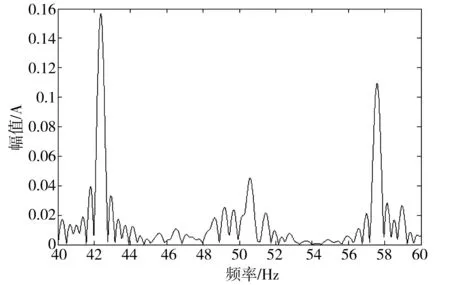
图9 LMS自适应滤波后的定子电流频谱图Fig.9 Spectrum of stator current after LMS adaptive filtering

从图9可以看到，LMS滤波后滤除了50Hz基波频率分量，在基波频率50Hz的两侧出现了2个明显的边频分量，读取频谱图中幅值最大处的频率分别为42.37Hz和57.58Hz，与根据转差率计算出的边频分量频率完全吻合，反映了LMS自适应滤波的效果。

4 结 论

通过以上分析可以得出如下结论：

1)LMS滤波用到了电压信号正、负半周的对称性，每个主频周期只有4个采样点，采样周期固定。

2)LMS法滤波对边频信号的等效采样周期随电机运行状态即转差率s变化，一般小于按主频信号设定的实际固定采样周期至少1个数量级。

3)LMS法滤波是按照等效采样周期在边频信号的多个周波分别采样，拟合出边频信号的1个完整周波，因而适用于电机运行状态及电流信号稳定的场合。

[1] DELEROI,W.Broken bar in squirrel cage rotor of an induction motor,Part 1: Description by superimposed fault currents[J].Archiwum Elektrotechniki,1984,67:91-99.

[2] KILMAN G B,STEIN J,ENDICOTT R D,et al.Noninvasive detection of broken rotor bars in operating induction motors[J].IEEE Transactions on Energy Conversion,1988,3(4): 873-879.

[3] GYFTAKIS K N,ATHANASOPOULOS D K,KAPPATOU J C.Broken bar fault diagnosis in single and double cage induction motors fed by asymmetrical voltage supply[C]// IEEE,9th IEEE International Symposium on Diagnostics for Electric Machines,Power Electronics and Drives,Universitat Politecnica de Valencia,August 27-30,2013,Valencia,Spain.DEMPED 2013: 402-406.

[4] RICARDO V N,JOSE J R M,JUAN M R C,et al.Empirical mode decomposition analysis for broken- bar detection on squirrel cage induction motors[J].IEEE Transactions on Instrumentation and Measurement,2015,64(5):1118-1128.

[5] 姜建国，汪庆生，杨秉寿，等.用自适应方法提取鼠笼式异步电机转子断条的特征分量[J].电工技术学报,1990(4):176-179． JIANG Jianguo,WANG Qinsheng,YANG Bingshou,et al.Applying the adaptive noise cancellation to extract the features of squirrel cage induction motor with rotor defects[J].Transactions of China Electrotechnical Society,1990(4):176-179.

[6] 邱阿瑞.用起动电流的时变频谱诊断鼠笼异步电机转子故障[J].中国电机工程学报,1995,15(4): 267-273. QIU Arui.Diagnosis of rotor fault in squirrel-cage induction motors using time-varying frequency spectrum of starting stator current[J].Proceedings of the CSEE,1995,15(4):267-273.

[7] JAWAD F,BASHIR-MAHDI E.A new pattern for detecting broken rotor bars in induction motors during start-up[J].IEEE Trans.Magnetics,2008,44(12):4673-4683.

[8] JOSE A D,MARTIN R G,JOAN P L,et al.Detection of broken outer-cage bars for double-cage induction motors under the startup transient[J].IEEE Transactions on Industry Applications,2012,48(5):1539-1548.

[9] 许伯强，李和明，孙丽玲，等.笼型异步电动机转子断条故障检测新方法[J].中国电机工程学报,2004,24(5):115-119. XU Boqiang,LI Heming,SUN Liling,et al.A novel detection method for broken rotor bars in induction motors[J].Proceedings of the CSEE,2004,24(5): 115-119.

[10] 许伯强,孙丽玲,李和明.基于高频率分辨力谱估计技术与优化算法的异步电动机转子故障检测新方法[J].中国电机工程学报,2013,33(3):140-147. XU Boqiang,SUN Liling,LI Heming.A detection method for rotor fault in induction motors based on high frequency resolution spectrum estimation technique and optimization algorithm[J].Proceedings of the CSEE,2013,33(3):140-147.

[11] MOHAMED S,ANTNIO J,MARQUES C,et al.The use of a modified Prony method to track the broken rotor bar characteristic frequencies and amplitudes in three-phase induction motors[J].IEEE Transactions on Industry Applications,2015,51(3): 2136-2147.

[12] LIN Wheimin,SU Tzujung,WU Rongching.Parameter identification of induction machine with a starting no-load low-voltage test[J].IEEE Transactions on Industry Electronics,2012,59(1): 352-360.

[13] ELHUSSEIN A M,HUSSIEN F S,MALIK E E.A sensorless induction motor drive using a least mean square speed estimator and the matrix converter[C] //IEEE,IEEE Industry Applications Society Annual Meeting(IAS),October 9-13,2011,Orlando.IAS 2011:1-7.

The features of LMS adaptive filter in rotor bar broken diagnosis of squirrel cage asynchronous machines

LIU Xin-zheng1， HE Sheng-hua1， GAO Lin1， ZHANG Hou-cheng2

(1.School of Electrical Engineering，Xi′an Jiaotong University，Xi′an 710049，China;2.Nanjing ThinkBon Electric Co.,Ltd.，Nanjing 211102，China)

For the diagnosis of rotor broken bar fault in squirrel cage asynchronous machines,spectrum analysis of stator current is often used to extract the side frequency components that represent the typical fault characteristics.To remedy the drawbacks existed in doing FFT spectrum analysis for the curent directly,which could make the side frequency components be overcovered by main frequency signal,the Least Mean Square (LMS) error adaptive filter algorithm was used prior to FFT analysis to filter main frequency signal and highlight the side frequency components.The LMS adaptive filter algorithm and the parameters determination in rotor broken bar fault diagnosis were given,and the sample features and the effective sample period for side frequency component at different operation slips were analyzed in detaile.The results show that,with LMS filter algorithm,when the stator current was sampled at a fixed sample period chosen according to main frequency,the side frequency component is actually sampled at the different point of its different individual waveform,and a full waveform is comopsed accrodingly.The effective sample period for side frequency component varies with slip and is smaller than the fixed one by an order of magnitude at least.

squirrel cage asychronous machine; rotor bar broken; spectrum analysis;least mean square; adaptive filter

2016-06-02

刘新正(1959—)，男，硕士，副教授，研究方向为电机分析及控制； 何升华(1989—)，男，硕士，研究方向为电机故障诊断； 高 琳(1962—)，女，硕士，副教授，研究方向为永磁同步电机控制； 张厚成(1973—)，男，高级工程师，研究方向为电机的监测与控制。

刘新正

10.15938/j.emc.2017.05.001

TM 343

A

1007-449X(2017)05-0001-07