基于偏最小二乘法的组合S型增长曲线预测模型与应用

程毛林

（苏州科技大学 数理学院，江苏 苏州 215009）

基于偏最小二乘法的组合S型增长曲线预测模型与应用

程毛林

（苏州科技大学 数理学院，江苏 苏州 215009）

在许多时间序列预测中，常用S型曲线描述增长过程。由于S型曲线形式多样，结构不同，对同样观测值预测，结果略有差别。为了增加预测精度，提高预测的可靠性，考虑不同增长曲线预测结果存在多重共线性，该文利用偏最小二乘法，建立组合S型增长曲线，实例表明组合S型增长曲线预测结果精度高。

增长曲线；非线性最小二乘估计；偏最小二乘法；预测精度；组合

在时间序列里，有些变量的增长量最初比较小，随时间的增加逐渐增长而达到一个快速增长时期，尔后增长速度趋缓，最终达到稳定的总增长量，这一过程若用曲线来表示，则是一种拉长的S型曲线。这种S型曲线因变量增长特性的不同而呈现出多样性变化。常用Richards、General Logistic、Von Bertalanffy、Morgan-Mercer-Flodin等生长模型来描述这种增长过程[1-7]。随着计算机仿真技术的应用，对增长模型的研究更加深入。对同样的数据，建立S型增长曲线的预测结果会略有差异，为了减小这种差异，笔者基于偏最小二乘法[8-12]，给出组合S型增长曲线预测模型。

1 S型增长曲线的形式

1.1 General Logistic模型

General Logistic模型形式为

或

式中，xt为t时刻某变量的观测值；s、α、λ、γ为待估参数。s为饱和水平，α为增长速度因子，λ为形状因子，γ为积分常数，ε为随机误差。当λ＝1，λ＝－1，λ→0时，可得到逻辑曲线、修正指数曲线、龚伯兹曲线。

与General Logistic模型结构相同的是Richards模型（可相互推导）。这一模型形式为

或

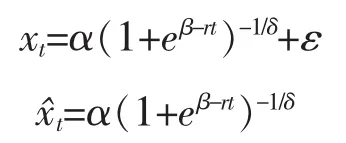
式中，参数α为饱和水平、β为初始值参数、r为增长速率参数、δ为曲线形状参数，ε为随机误差。当δ=-1时为Mitscherlich模型，当δ→+∞时为Gompertz模型，当δ=1时为Logistic模型。因此，Richards模型对S型增长时间序列有很强的适应性。

1.2 Von Bertalanffy模型

Von Bertalanffy模型具体形式为

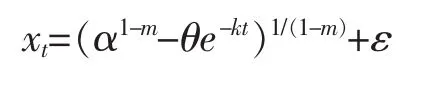
或

式中，α、θ、k、m为待估参数。ε为随机误差，α为饱和水平，k为增长速度因子，m为形状因子，θ为积分常数。

当m=0时为修正指数曲线，m=2时为逻辑曲线，m→1时趋向于龚伯兹曲线。

1.3 Morgan-Mercer-Flodin模型

Morgan-Mercer-Flodin模型形式为

或

上式，待估参数为η=（β，r，α，δ）。显然，当δ＜0，t→+∞时，y→β；当δ＞0，t→+∞时，y→α。

1.4 三角函数增长曲线模型

主要有正弦函数增长曲线模型和余弦函数增长曲线模型。正弦函数增长曲线模型形式为

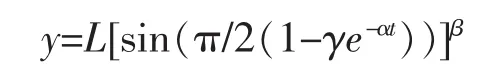
其中，L、α、β、γ为待估参数。L为饱和水平，α为增长速度因子，β为形状因子，γ为积分常数。显然t→+∞时，y→L。

余弦函数增长曲线模型形式为

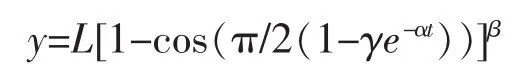
其中，L、α、β、γ为待估参数。L为饱和水平，α为积分常数，β为增长速度因子，γ为形状因子。显然t→+∞时，y→L。

1.5 Weibull模型

Weibull模型形式为

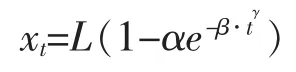
上式，待估参数为η=（L，α，β，γ）。L为饱和水平，α为增长速度因子，β为形状因子，γ为积分常数。显然t→+∞时，y→L。

2 组合S型增长曲线

2.1 S型增长曲线模型的参数估计

对线性模型的参数估计可直接使用最小二乘法，不需要确定参数初始值。但上面的5个S型增长曲线是本质上的非线性曲线。每个模型都含有4个参数，参数估计比较复杂，记某个S型增长曲线为

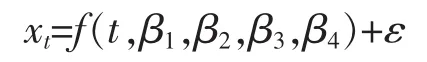
其中，f是自变量t以及个参数β1、β2、β3、β4的非线性函数。估计参数β1、β2、β3、β4的标准与线性回归一样，即误差平方和最小化。如果具有x以及t的N个观测，就让

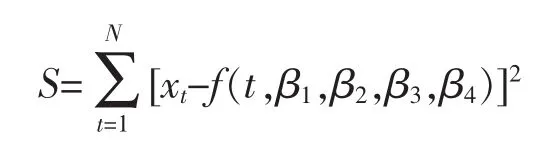
有最小值，即为非线性最小二乘估计[13-15]。一般利用软件，如MATLB软件求解。初始值的确定可用选点法，对含4个参数的非线性曲线，设选取的4个点为，代入得到一个非线性方程组

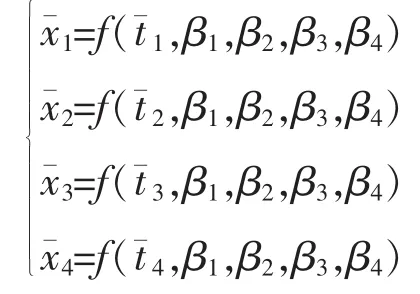
利用MATLB软件可以求出初始值β1、β2、β3、β4[16]。

2.2 组合S型增长曲线模型

假设文中选择5个S型增长曲线，分别为X1、X2、X3、X4、X5。显然X1、X2、X3、X4、X5之间存在严重的多重共线性，笔者利用偏最小二乘回归建立组合增长曲线模型。将X1、X2、X3、X4、X5视为5个自变量，因变量为Y，进行偏最小二乘回归。该文这里给出一个简洁的计算方法：

设自变量X＝（X1，X2，…，X5）和因变量Y标准化处理后的数据为E0、F0。

（1）求矩阵E0TF0F0TE0最大特征根所对应的特征向量w1，求得成分得分向量，和残差矩阵，其中

（2）求矩阵E1TF0F0TE1最大特征根所对应的特征向量w2，求得成分得分向量，和残差矩阵，其中

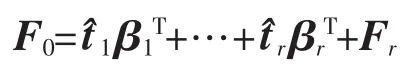
把tk=wk1*X1*+…+wk5*X5*（k=1，2，…，r）代入Y*=t1β1+…+trβr，即得偏最小二乘回归方程为

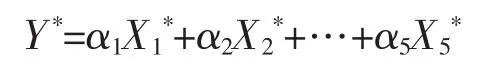
用原始变量表示的组合增长曲线模型为

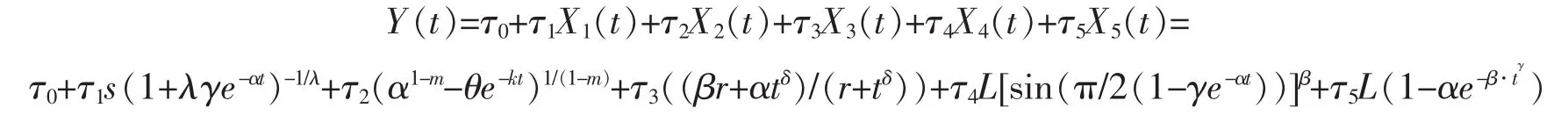
3 组合S型增长曲线预测模型应用

根据中国互联网信息中心提供的中国互联网络发展状况统计报告，收集了自2008年6月至2015年每半年一次的网民人数数据（x），见表 1。分析可知数据呈S型增长。

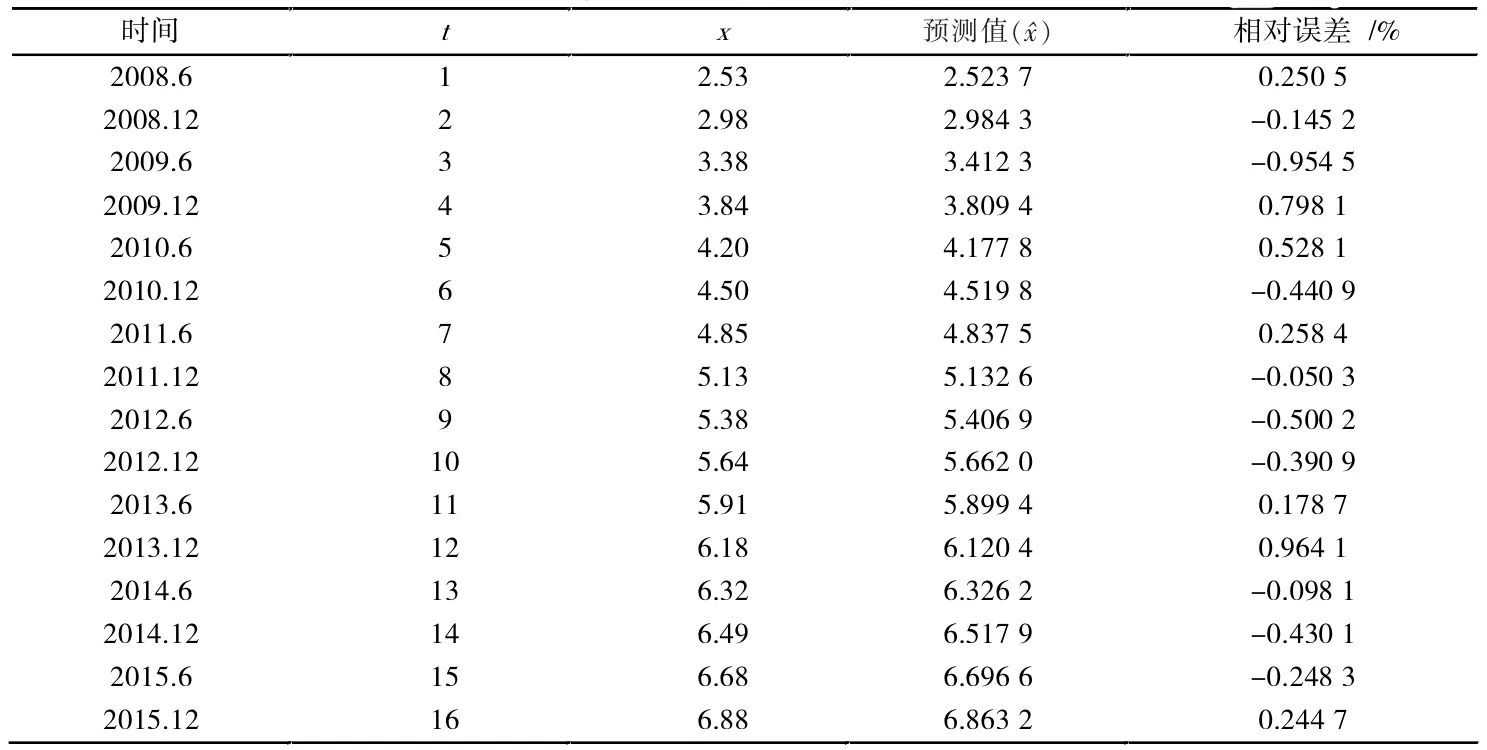
表1 中国网民人数及相关结果

先分别建立5个增长曲线模型：

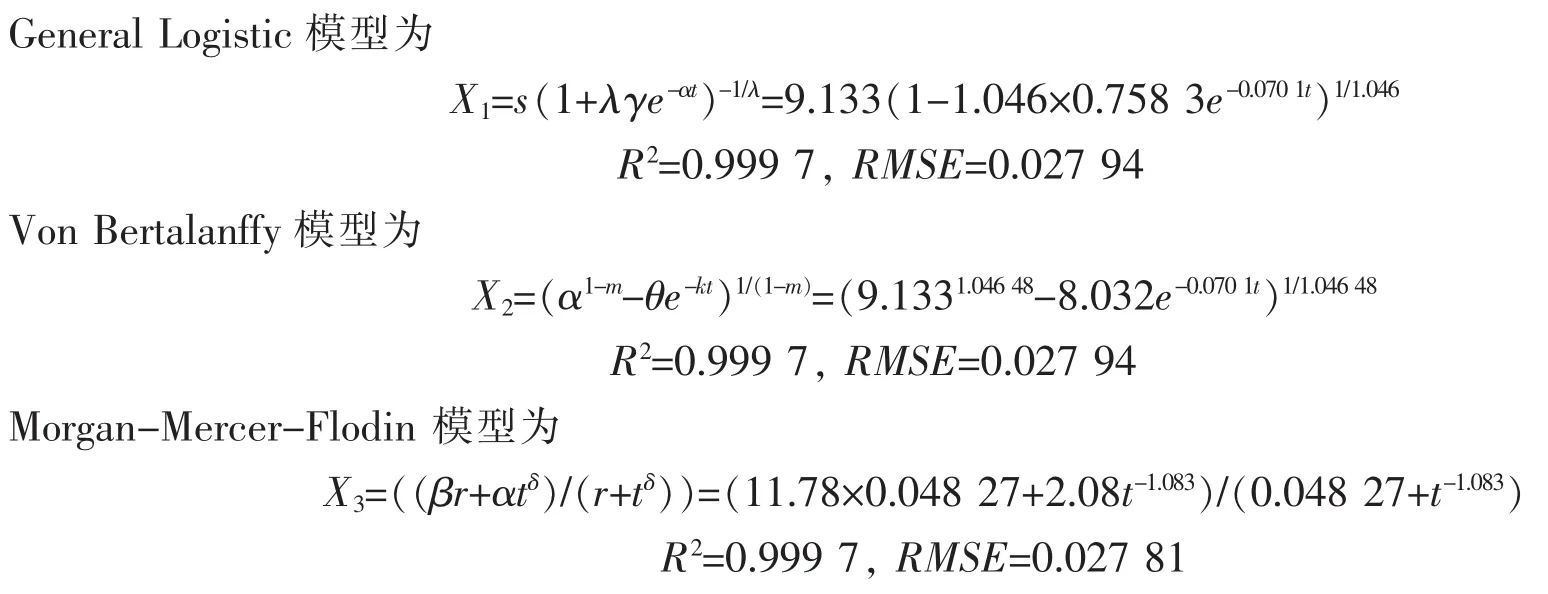
正弦函数增长曲线模型为

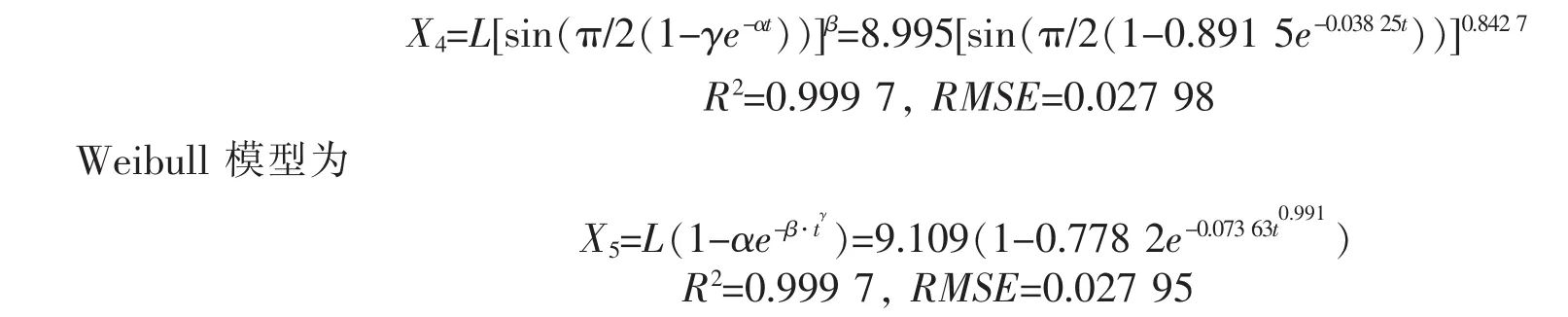
将X1、X2、X3、X4、X5视为5个自变量，因变量为Y，作偏最小二乘回归，得预测模型

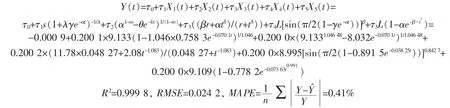
从检验量可以看出模型拟合精度很高。图1给出了拟合图，图中星号为实际观测点，实线为拟合曲线。

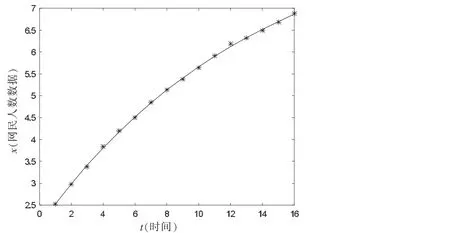
图1 模型拟合图

[1]LIN Zhaogang，LI Fengri.The generalized Chapman－Richards function and applications to tree and stand growth[J].Journal of Forestry Research，2003，14（1）：19-26．

[2]PAN Jianxin，FANG Kaitai.Growth Curve Model and Statistical Diagnostics[M].New York：Springer-Verlag，2002.

[3]程毛林.Richards模型参数估计及其模型应用[J].数学的实践与认识，2010，40（12）：139－143．

[4]程毛林.二个四参数增长曲线模型参数初始值的确定方法与模型应用[J].数学的实践与认识，2009，39（9）：109-114.

[5]程毛林.逻辑思谛曲线的几个推广模型与应用[J].运筹与管理，2003，12（3）：85-88.

[6]刘舒燕，艾书超.基于增长曲线模型的高速公路发展研究[J].武汉理工大学学报（交通科学与工程版），2004，28（3）：365-368.

[7]刘磊.逻辑增长曲线模型的一种参数估计方法[J].湖北工业大学学报，2008，23（1）：83-85.

[8]马丽，吕成文，唐炎.基于偏最小二乘法的土壤有机碳高光谱预测研究[J].安徽师范大学学报（自然科学版），2016，39（2）：164-167.

[9]卢鹏，何杰，彭丛笑.基于偏最小二乘法的PM2.5相关因素分析研究[J].四川理工学院学报（自然科学版），2015，28（1）：71-75.

[10]司守奎，孙玺清.数学建模算法与应用[M].北京：国防工业出版社，2012.

[11]陈章华，陈磊，纪洪广.基于偏最小二乘法的地应力场拟合[J].北京科技大学学报，2013，35（1）：1-7.

[12]郑鸣，段梅，陈福生.我国金融发展与外资企业自主创新——基于偏最小二乘法的实证研究[J].软科学，2012，26（8）：1-5.

[13]李海奎，王雪峰.基于符号运算和信赖域方法的非线性最小二乘法[J].计算机应用，2004，24（7）：22-24.

[14]陈忠，黄惠.求解非线性最小二乘问题的迭代法[J].武汉大学学报（理学版），2003，49（1）：14-16.

[15]XIAO Ailing.Some algorithms of nonlinear least squares[J].Mathematical Theory and Applications，2004，24（2）：86-90.

[16]薛西峰，邢志栋，孟红云.求解非线性方程组的信赖域方法[J].西北大学学报（自然科学版），2001，31（4）：289-291.

Prediction model and application of combined S-type growth curves based on partial least squares

CHENG Maolin
（School of Mathematics and Physics，SUST，Suzhou 215009，China）

In many time series prediction,researchers commonly use S-type curves to describe the growth process.Because of the diversity of S-type curves and the differences in their structures,the results are slightly different out of the same observation.In order to improve the prediction accuracy and reliability，the author,taking into consideration the prediction results of different growth curves with multicollinearity，established the combined S-type growth curves with partial least squares.The illustrations show that the prediction accuracy of the combined S-type growth curves is high.

growth curve；nonlinear least squares estimation；partial least squares；prediction accuracy；combination

责任编辑：谢金春

O212MR（2010）Subject Classification：62J02

A

：2096－3289（2017）02－0008－04

2016－11－06

国家自然科学基金资助项目（11401418）

程毛林（1965-），男，安徽安庆人，副教授，硕士生导师，研究方向：应用统计。