正弦绕组分布下单相感应电机二维有限元分析
付 敏,于 静,宋瀚生
(1.哈尔滨理工大学,哈尔滨150080;2.哈尔滨电机厂有限责任公司,哈尔滨150046)
0 引 言
单相电机中存在大量谐波磁势,导致电机性能降低,如谐波使设备产生附加的铜耗和铁耗,引起电机发热,甚至烧毁,导致绝缘强度降低,同时产生较大噪声[1]。由于高次谐波对电机造成上述影响,所以研究如何消除或削弱谐波具有重要的意义。
为了改善单相电机的性能,较多采用正弦绕组的方法来削弱谐波磁势[2]。文献[3]为了改善圆筒型永磁直线电机气隙磁密波形的正弦性并提高其推力性能,分别从槽极数配合、绕组分相、初级铁心长度等方面系统地分析了各参数对电机性能的影响,最终确定圆筒型永磁直线电机结构参数。文献[4]针对三相异步电动机,分析了其表面损耗、齿部脉振损耗、转子谐波损耗、横向泄漏电流损耗,并针对正弦绕组、槽配合、气隙长度、铸铝工艺的设计参数选择,分析了降低杂散损耗的措施。文献[5]针对圆筒型永磁同步直线电机,设计了无刷直流式、交流正弦式和模块化3种绕组方式,分析3种绕组下的气隙磁密波形、三相绕组磁链曲线、三相绕组反电动势曲线及定位力波动曲线,通过对比得到3种绕组的优点与缺点。
现有文献较多是定性分析正弦绕组优点,但正弦绕组相较于普通绕组优势的详细数据还鲜有文献涉及。基于此,本文通过对一台单相感应电机的磁场进行二维有限元数值仿真计算,分析采用正弦绕组时气隙磁密谐波下降的比率。
1 正弦绕组
绕组作为电机的重要组成部分,直接决定着电机运行性能。不同的绕组形式,起到不同的作用,合理的绕组类型可以有效地提高电机效率,改善电机的运行性能。目前叠绕、同心式绕组以及单双层混合式绕组等绕组方式被广泛应用于电机中[6]。由于正弦绕组可以消除或者削弱气隙磁密中的谐波,减小电机的损耗,所以正弦绕组得到更广泛的应用[5]。
正弦绕组是一种较高精度的绕组形式,从自身结构来说,它能够结合单层绕组和双层绕组的优点,有效地消除或抑制高次谐波。从电磁设计的角度考虑,它能够灵活地选择每层每槽匝数。由于每极每相槽数之间的匝数差较大,使极相组的串联匝数可以实现微调,而普通式绕组由于不具备这样的性能,所以在使用过程中会受到很大的局限。
2 单相感应电机模型的建立
2.1 电机二维几何模型的建立
根据二维静态磁场理论,采用有限元分析软件,建立单相感应电机二维模型。在Maxwell工作界面直接绘图时需注意,由于其是依据点线面进行建模的,为此需把建立某封闭图形的每一条线段都连接起来,组成一个封闭的面,进而生成需要的面域[7]。定子齿槽内的绕组分为工作绕组和副绕组两部分,绘制绕组时需分开绘制。单相感应电机冲片基本参数如表1所示。
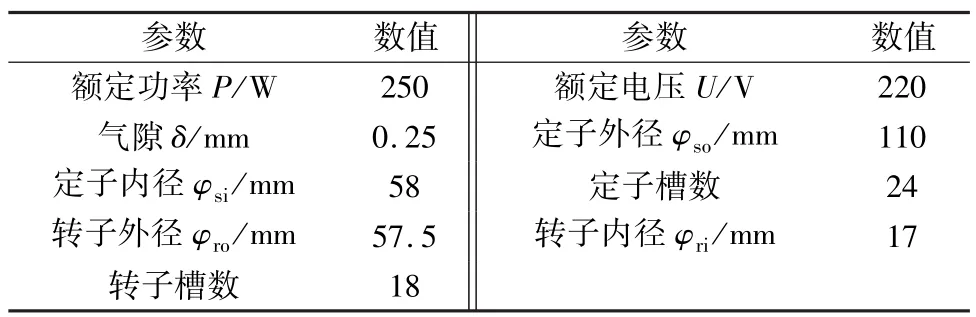
表1 样机的主要技术参数
根据表1中的参数,建立单相感应电机二维几何模型如图1所示。单相感应电机定、转子铁心由硅钢片叠压制成,定子槽有两层绕组,分别为主绕组和副绕组。
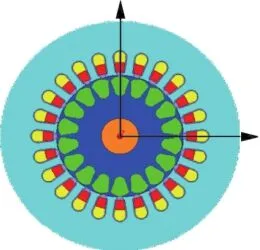
图1 单相感应电机二维模型
2.2 绕组排列方式
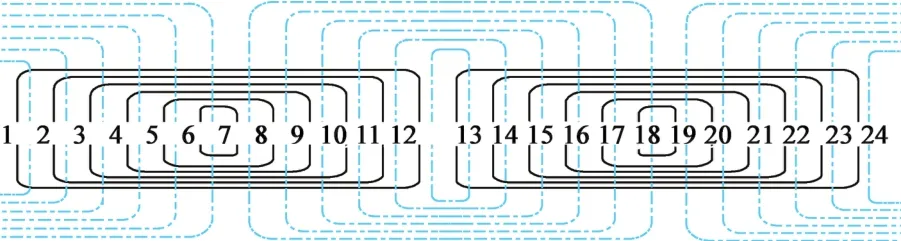
图2 同心式双层绕组
电机绕组缠绕方式如图2所示。图中实线表示主绕组,虚线为副绕组。确定电机的绕组排布,选择工作绕组,右键找到Assign Excitation/Current Destiny分别在绕组中输入电流密度,输入电流密度为Jz,计算公式:

式中:S为载流线圈横截面积;N为线圈匝数;i为每匝通过的电流,正值表示电流方向为Z轴正方向,负值表示电流方向为Z轴反方向。
单相感应电机通电后产生脉动磁场,无法实现转子起动。为此需添加一个在空间上与工作绕组相差90°的辅助绕组(副绕组),同时辅助绕组内的电流与工作绕组内电流在幅值上相等,但在相位上相差90°,以保证在气隙中形成旋转磁场,实现电机的起动。
2.3 电机计算模型的建立
利用有限元分析该电机磁场时,为了简化分析,不考虑磁场在轴线方向上的变化,因此可将三维空间分布简化为二维平面分布。在二维场分析中采用如下假设:1)忽略位移电流及其影响;2)忽略定子轭背部的漏磁通;3)忽略磁饱和。由矢量磁位Az表示的单相感应电机满足的电磁场方程:
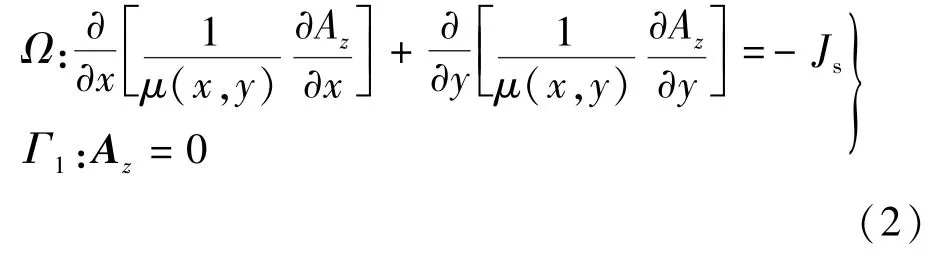
式中:Js为源电流密度;μ(x,y)为介质有效磁导率;Az为矢量磁位z轴分量;Γ1为第一类边界条件,在本例中即为定子外圆。
2.4 网格剖分
网格剖分是有限元计算分析的基础,网格的剖分程度直接影响到有限元的计算精度[8]。由于三角形单元剖分使计算所得的多项式形函数对于各个节点的利用率最高,所以对求解场域进行剖分时,将单元选择为三角形,得到剖分图如图3所示。
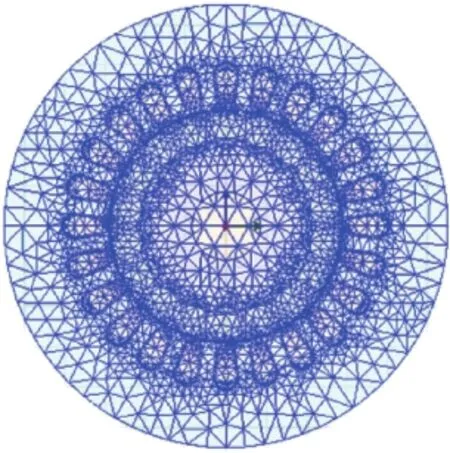
图3 单相感应电机剖分图
3 电机磁场有限元分析
电机绕组有多种形式,本文分别采用普通式绕组和正弦式绕组,通过对不同绕组形式下的电机磁场进行仿真,并对比两种绕组下的气隙谐波分量。
3.1 普通同心式绕组的电磁场分析
采用普通同心式绕组时,每个绕组中线圈匝数均相同,由式(1)可知,此时各个线圈中的电流密度数值相同。基于有限元法对采用普通同心式绕组的电机磁场进行仿真计算,得到磁场分布,如图4所示。
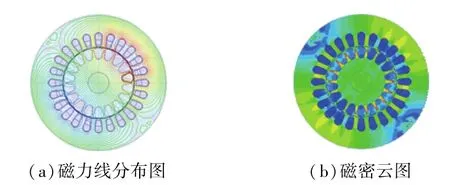
图4 磁力线分布图及磁密云图
从图4中可看出,电动机中定子与转子之间产生的磁场变化主要表现在气隙磁密上。为进一步分析此时的气隙磁密分布,基于Ansoft后处理功能计算气隙磁密,并通过MATLAB进行傅里叶分解,得到气隙磁密随空间角度变化的情况,如图5所示。
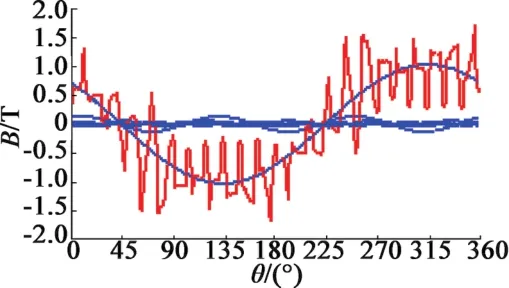
图5 气隙磁密图
由图5可知,气隙磁密基波分量所占比重大,为磁密主要组成部分。因为电机定子齿槽的存在,导致实际得到的曲线存在波动。磁密中除了含有其主要作用的基本分量外,还含有较多其他谐波分量。
3.2 正弦式绕组的电磁场计算
正弦式绕组与普通同心式绕组的不同之处在于:为得到更好的正弦分布,选取最接近正弦的一组数据,按照此比例选取匝数,分配到定子槽中,使定子绕组产生的磁动势在空间分布尽可能是一个正弦波[9]。
与采用普通同心式绕组相同,图6为采用正弦式绕组时的磁场分布,图7为经过傅里叶分解得到的气隙磁密随空间角度变化的情况。
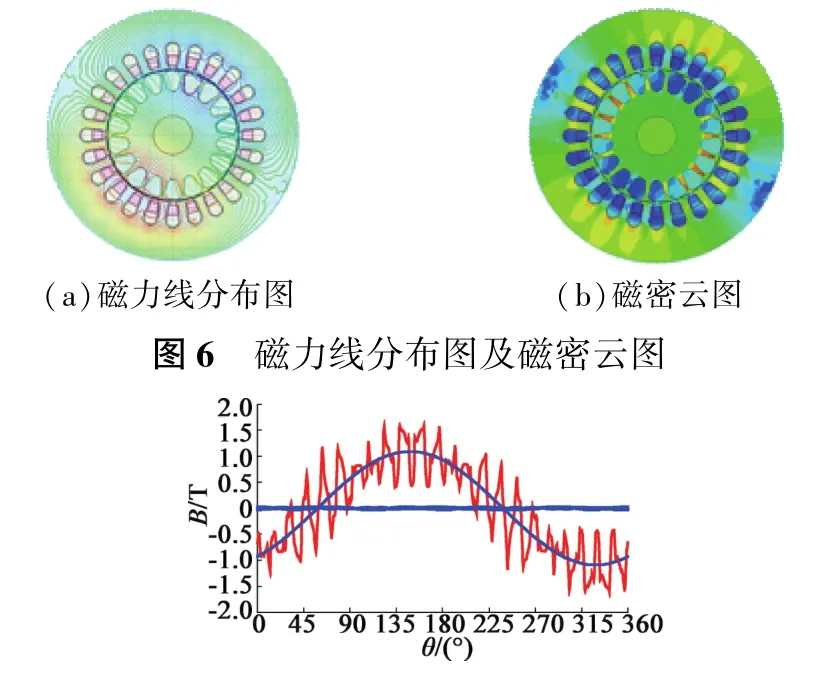
图7 气隙磁密图
由图7可知,正弦式绕组得到的磁密更接近于正弦分布。正弦绕组下的气隙磁密中除了含有起主要作用的基波分量外,其他谐波分量减小。
3.3 气隙谐波的频谱分析
为了能够更加明显的看到正弦式绕组与普通同心式绕组形式下的谐波分量幅值,分别对两种气隙磁密进行频谱分析,得到两种状态下的谐波分量的幅值,将得到的谐波幅值进行对比,如图8所示。
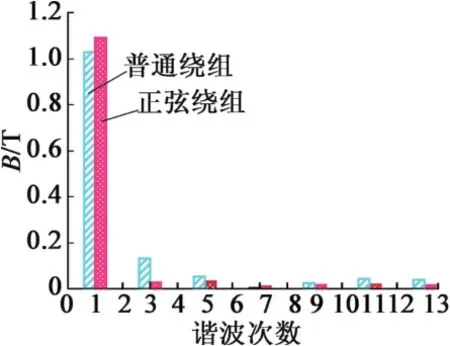
图8 两种绕组下的气隙谐波含量
由图8可知,电机采用正弦绕组时,基波分量高于普通同心式绕组基波分量,同时3,5,9,11等奇次谐波幅值低于采用普通同心式绕组时的谐波幅值。
通过对图8中不同谐波次数的幅值进行计算,得到本文中两种不同绕组分布下各次谐波所占百分比,如表2所示。
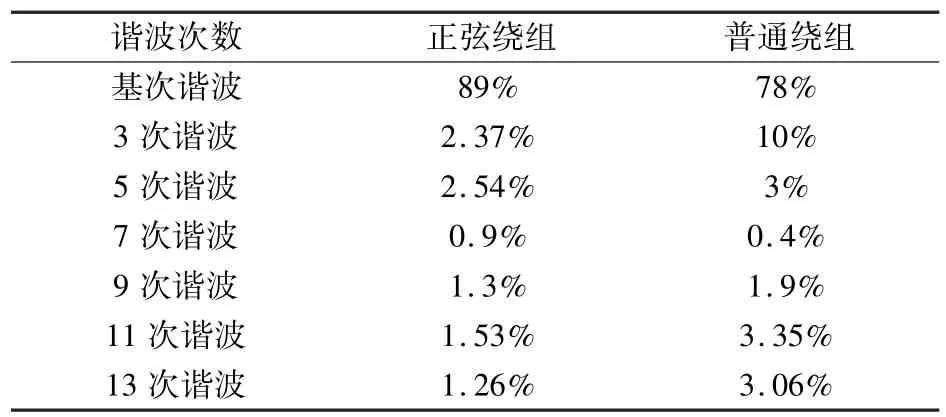
表2 两种不同绕组分布下各次谐波所占百分比
由表2可知,通过对谐波幅值的计算和对比,得出采用正弦式绕组时基波分量所占比重更大,低阶次谐波分量的幅值大于高阶次谐波分量幅值。通过定量的分析计算,得出正弦式绕组能有效地抑制谐波,具有更优越的性能。
4 结 语
本文从单相感应电机本体出发,通过改变绕组的电流密度,从而改变绕组的接线方式,在有限元的基础上,不再定性的分析正弦绕组对电机气隙磁密的影响,而是定量的分析正弦绕组在抑制谐波方面的优越性。并得到以下结论:
(1)电机采用正弦式绕组时得到的气隙磁密更接近正弦分布。
(2)采用正弦式绕组时,基波分量幅值增加,其他谐波幅值明显降低,并且基波分量所占比重增加,谐波得到有效抑制。
参考文献
[1] 赵海森,王博,王翔宇.过电压条件下谐波磁场对异步电机附加损耗的影响[J].电机与控制学报,2014,18(8):1-7.
[2] 彭晓,陈意军.再论单相电机正弦绕组设计[J].微特电机,1992,19(6):11-13.
[3] 崔皆凡,李一,刘旭.圆筒型永磁直线电机的设计及有限元分析[J].微电机,2016,49(5):25-27.
[4] 宁榕,李巧莲,黄坚,等.三相异步电动机的杂散损耗研究[J].电机与控制应用,2014,41(5):14-18.
[5] 刘星桥,黄新光,王燕,等.圆筒型永磁同步直线电机绕组分析[J].电机与控制应用,2013,40(3):8-12.
[6] 刘昌奇,徐余法,李全峰,等.基于有限元分析的一种超超高效异步电机[J].电机与控制应用,2015,42(5):75-80.
[7] 王振,刘建国,王爱凤,等.基于ANSOFT的永磁同步电机有限元分析[J].能源研究与管理,2010(3):26-27,33.
[8] 王芳,陈小军.基于Ansoft的高速永磁无刷直流电机磁场有限元分析[J].南昌大学学报(工科版),2012,34(4):387-389,395.
[9] 周秀红.磁悬浮球形电动机的机理与控制[D].扬州:扬州大学,2008.
[10] LIAO W D,LUO L F,LUO D R,et al.Starting process simulation of Smith single-phase capacitance motor[C]//Proceeding of International Conference on Electronic Communication Control,2011:1040-1043.
[11] GONZALEZ A,HERNANDEZ C,ARJONA M A.A novel highefficiency parallel-winding connection for a three-phase induction motor fed by a single-phase power supply[J].IEEE Transactions on Energy Conversion,2014,29(2):269-277.
[12] 李勇,吕鑫源,樊华,等.永磁齿轮耦合的特殊问题的仿真分析[J].微电机,2016,49(7):23-27.

