利用测井资料预测水平井压裂裂缝形态
谢刚, 罗利, 刘向君, 梁利喜, 姜巍, 常俊
(1.中国石油川庆钻探工程公司测井公司, 重庆 400021; 2.西南石油大学油气藏地质及开发工程国家重点实验室,四川 成都 610051; 3.中国石油川庆钻探工程公司页岩气勘探开发项目经理部, 四川 成都 610051)
0 引 言
测井资料常用于预测直井双翼压裂裂缝的裂缝高度[1-2]。与常规直井压裂相比,水平井井斜角较大,钻遇地层情况复杂,井周应力场分布、裂缝起裂、裂缝延伸规律与直井有很大不同,压裂裂缝形态更加复杂,不仅有纵向缝、横向缝,还有转向缝和复杂多裂缝等,预测难度较大[3-5]。Hossain等[6]建立了射孔完井和裸眼完井条件下直井和水平井的纵向裂缝、横向裂缝和复杂多裂缝的封闭式解析解,组合成数值模型分析压裂裂缝的延伸动态。Dahi Taleghani[7]利用扩展有限元法进行了页岩储层天然裂缝条件下的水力压裂裂缝扩展模拟,对直井进行计算。Olson[8]利用边界元理论建立了水平井多段压裂的裂缝扩展模型。Weng等[9-10]提出了非常规压裂裂缝扩展模型。赵金洲等[11]建立了复杂裂缝网络模型,实现了对含有大量天然缝的页岩气藏压裂裂缝网络的模拟研究。解析法、扩展有限元法、边界元法、非常规裂缝扩展模型等方法作为页岩气水平井常用的裂缝延伸扩展分析方法,都有其优缺点和适用性,需要进一步改进和完善,才能真实地模拟页岩气水平井复杂裂缝扩展[12]。
本文研究了用测井资料预测水平井压裂裂缝形态的方法以及用测井资料计算四川页岩气水平井岩石力学参数和地应力的方法,建立了水平井压裂裂缝起裂数学模型;考虑井周裂缝应力、流体的实际状态,根据断裂力学理论给出了水平井井周裂缝尖端的应力强度因子的计算方法,建立了裂缝延伸扩展模型;提出了用测井资料预测压裂裂缝长宽高的方法,建立了用测井资料预测水平井压裂裂缝的方法。对四川页岩气水平井H1-3井压裂裂缝形态进行了预测并与微地震监测结果进行对比,表明预测结果能够反映近井周围压裂裂缝的延伸情况。
1 四川页岩气水平井岩石力学参数和地应力计算
1.1 岩石力学参数
岩石力学参数和地应力是压裂模拟和优化设计的重要输入参数,对压裂裂缝的延伸扩展有重要影响[13-14]。根据阵列声波测井的波形分析所提供的纵波、横波时差,结合密度测井资料可以计算出地层任一深度的弹性模量、泊松比、体积模量、体积压缩系数等岩石力学参数[15-16]。
实际生产中,四川页岩气水平井主要进行常规测井,横波时差的估算分析对计算岩石力学力学参数尤为重要。四川页岩气储层矿物复杂,包括黏土、石英、长石、方解石、白云石、黄铁矿和大量的有机质,采用复杂多矿物组分模型预测地层横波时差[17-18]。
岩石的断裂韧性用来衡量岩石阻止裂纹扩展延伸的能力,与岩石自身的力学特性密切相关,可由实验测试分析获取。研究表明[19],若忽略裂缝中的摩擦损失,假定裂缝中的流体压力等于井眼流体压力,则对于Ⅰ型裂缝,岩石的断裂韧性可表示为
(1)
其中
Sx=pw-pp
(2)
(3)
式中,KIC为岩石I型裂缝断裂韧性,MPa·m1/2;Sx为井壁压力差,MPa;Tx为岩石单轴抗压强度,MPa;E为岩石弹性模量,MPa;h为裂缝半长,m;pw为井底压力,MPa;pp为地层孔隙压力,MPa;B为岩石的体积压缩系数,MPa-1;Vsh为岩石黏土含量,无因次。
对于Ⅱ型裂缝,已有研究表明,断裂韧性可由抗张强度、围压利用式(4)得到[19]
KIIC=0.0466pc+0.1674St-0.1851
(4)
式中,KIIC为岩石Ⅱ型裂缝断裂韧性,MPa·m1/2;pc为围压,MPa;St为单轴抗张强度,MPa。
断裂韧性一方面取决于岩石自身的力学性能;另一方面还与赋存的围压条件、井底流体压力等因素密切相关。对不同岩性地层、不同的围压环境,针对性地开展物理实验,建立相应的评价模型是实现断裂韧性测井准确评价的基础。对于Ⅱ型、Ⅲ型裂缝的延伸以及层理面、天然裂缝等结构面的情形可采用上述相同思路由断裂力学理论进行分析。
1.2 三轴地应力
针对水平井,用密度测井资料计算垂直应力的公式为

(5)
式中,SV为总垂直应力,MPa;D为深度,m;g为重力加速度,m/s2;θ为井斜角,(°);ρb为岩石体积密度,g/cm3;poffset为偏移值,MPa。
根据测井资料以及四川岩心地应力测试成果和压裂资料建立最大、最小水平应力的计算模型[20]。
2 水平井压裂裂缝形态数值模拟方法
在压裂作业过程中,随着压裂液的注入,裂缝在长、宽、高3个方向上起裂延伸,裂缝三维尺寸同时发生变化,最终在压裂目的层产生1个或多个具有一定导流能力的油气通道。
2.1 水平井压裂裂缝起裂数学模型
裂缝的起裂压力不仅与水平井井筒方位角(水平井筒水平段轴向与最大水平主应力方向之间的夹角)有关,还与井筒周围的岩石性质和井筒周围应力分布有关。预测与计算裂缝起裂可分为2步:①计算井筒周围的应力分布;②根据岩石破坏准则,当井筒应力大于岩石扩拉强度,裂缝起裂。
2.1.1 水平井井周应力场分布
基于Hossain给出的斜井井筒应力分布计算模型[6,21-22]并添加压裂液渗滤效应引起的附加应力,得到柱坐标系下水平井井筒水平段任意一点处的应力分布为
(6)
式中,σr为井筒径向应力,MPa;σθ为井筒切向应力,MPa;σz为井筒轴向应力,MPa;τrθ、τθz、τrz分别为井壁处剪应力分量,MPa;pm为井筒内压裂液压力,MPa;γ为渗透性系数,地层可渗透时γ=1,地层不渗透时γ=0;φ为岩石的孔隙度,无因次;pp为地层初始孔隙压力,MPa;μ为岩石泊松比,无因次;θ为射孔方位角,(°);α为Biot多孔弹性系数,无因次。
2.1.2 裂缝起裂判定准则
关于裂缝起裂的判定准则,张应力破坏准则认为裂缝起裂压力和起裂角取决于主应力分布状态。对于一个任意方向的井眼,3个主应力σ1、σ2、σ3中σ3在井壁处引起最高张应力可表示为
(7)
式中,σ1、σ2、σ3分别为最大、中间和最小主应力,MPa。
为了求出最大拉伸应力,对式(7)求导得
(8)
式中,θ为裸眼完井时裂缝的起裂角,(°)。
根据张应力破坏准则,当井壁处z—θ平面下的最大拉伸应力达到岩石的抗拉强度σt时,岩石破裂,即
σmax(θ)≥σt
(9)
2.2 裂缝延伸数学模型
2.2.1 页岩气水平井应力强度因子计算
依据断裂力学理论,考虑井周裂缝应力、流体的实际状态,井周裂缝尖端的应力强度因子通常由3部分构成,即裂缝壁面正应力所产生的应力强度因子、裂缝面流体压力所产生的应力强度因子以及流体界面张力产生的应力强度因子。
(1) 裂缝壁面正应力所产生的应力强度因子
(10)
式中,KI1为裂缝壁面正应力所产生的应力强度因子,MPa·m1/2;σ为裂缝面正应力,MPa;H为裂缝半高,m;y为距裂缝面长度,m。
(2) 裂缝面流体压力所产生的应力强度因子
(11)
式中,KI2为裂缝壁面流体压力所产生的应力强度因子,MPa·m1/2;pf为裂缝面所受的流体压力,MPa。
(3) 流体界面张力产生的应力强度因子。对于界面张力,P.S.Laplace and T.Young在1806年采用了双曲率的概念并提出了用以描述基质吸力与交界面几何尺寸之间关系,即杨-拉普拉斯方程
(12)
式中,F为界面上的附加吸力,在毛细管中,该附加吸力也称为毛细管力,N/m2;κ为液体界面张力,N/m;R1、R2分别为任意简单曲面的2个主曲率半径,m。
对于井眼周围的微裂缝裂尖,润湿性钻井液在缝尖产生的界面张力沿着液面切线方向指向凹液面(见图1)。

图1 锥形管中的液体界面张力
由几何关系知,当液体为润湿性介质时,毛细管力F为
(13)
当液体为非润湿性介质时,毛细管力为
(14)
式中,γ为液体界面张力,N/m;W为裂缝宽度,mm;β为裂缝壁与毛细管力中心线的夹角,(°),等于锥角的1/2;θ为润湿角,(°)。
界面张力γ沿着壁面的切向力γcosθ对Ⅱ型断裂有贡献,两侧壁上的正应力γsinθ则对Ⅰ型断裂有贡献
(15)
式中,KI3为两侧壁上的正应力所产生的应力强度因子,MPa·m1/2;l为裂缝长度,m。
由叠加原理可得裂缝尖端应力强度因子
(16)
式中,KI为裂缝尖端的应力强度因子,MPa·m1/2。
2.2.2Irwin延伸扩展准则
随着井筒内压力继续增大,裂缝将进一步延伸,缝高也进一步增大。根据Irwin断裂力学理论,当应力强度因子达到临界值即断裂韧性时,裂缝发生扩展延伸,裂缝扩展延伸可由式(17)进行判别[23]
KI≥KIC
(17)
式中,KIC为材料的断裂韧性,MPa·m1/2。
2.2.3 压裂裂缝长宽高的测井预测方法
假设条件:①设定地层是均质、各向同性的连续线弹性体;②储层厚度较大不发生穿层现象;③裂缝在垂直方向上的延伸速度小于在长度方向上的延伸速度。
压裂裂缝形态预测包含的控制方程:①起裂与延伸判定公式见式(9)、式(16);②压裂裂缝缝高预测见文献[24];③压裂裂缝缝宽预测方程。
当裂缝达到扩展条件后裂缝延伸,根据线弹性理论,井壁处压裂缝截面最大宽度有[25]
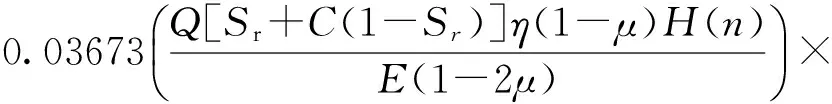
(18)
式中,Wmax为n次加压后的裂缝最大宽度,m;Q为排量,m3/min;Sr为砂比,无因次;C为压力液利用系数,无因次;H(n)为n次加压后的裂缝高度变化量,m;η为压裂液黏度,cP*非法定计量单位,1 cP=1 mPa·s,下同。
假设将压裂液注入地层需要的时间为t,在每个间隔注入相同体积的压裂液,压裂液在裂缝中的体积为
(20)
式中,V是压裂液在裂缝中的体积,m3。
假设压裂缝形状均为以缝高为长轴、以平均缝宽为短轴的椭圆为底、以缝长为高的椭球体,其体积为
(21)
裂缝的长度L可以表示为
(22)
2.2.4 压裂裂缝形态预测流程
裂缝起裂、延伸模型结合裂缝长宽高的预测方法,压裂裂缝形态预测流程如下:
(1) 输入井眼轨迹、岩石力学参数、地应力等地质参数。
(2) 输入排量、砂比、压裂液黏度等区域压裂参数。
(3) 设定最大泵压pw,max、泵压增量Δp及X、Y、Z方向裂缝扩展步长ΔL以及方位角搜索步长Δd。
(4) 计算井周应力场。
(5) 根据缝长、缝宽方程预测裂缝宽度W、裂缝长度L。
(6) 依据前述理论、计算模型逐点分析压裂井段内各深度点处的地层破裂压力及最小主应力,分析确定起裂点位置及起裂方位角。
(7) 根据前述方法,对裂缝端部0°~360°逐方位点计算应力强度因子KI及断裂韧性KIC。
(8) 逐方位点判断是否满足扩展准则,如果满足则令Li=Li-1+ΔL,di=di1+Δd。
(9) 如果Li>L,则程序结束,否则记录新的裂缝尖端的点的坐标信息,重复步骤(7)~(8)。
(10) 若各方位点均不满足扩展准则,则令p=pi+Δp。
(11) 若泵压p不大于设定的最大泵压pw,max,则重复步骤(7)~(10);否则,程序结束。
3 裂缝形态预测及与微地震监测结果的应用实例对比
四川页岩气水平井H1-3井位于威远中奥顶构造南翼,最大井斜角对应的井深3 700.00 m,其水平井轨迹示意图见图2。分析针对该井第1压裂段(5 090~5 180 m,段长90 m)的压裂裂缝形态进行预测。
H1-3井测井资料表明水平最大主应力方向为90°,即最大水平主应力应力方向为EW向。利用测井资料计算了H1-3井地层岩石力学参数、地应力等模拟输入参数(见图3、表1)。
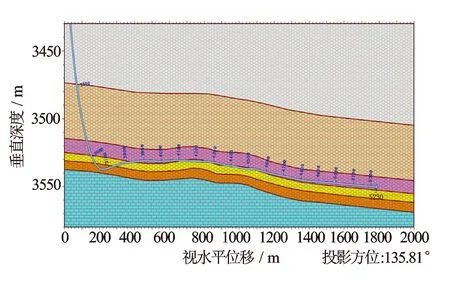
图2 H1-3井水平井轨迹示意图

图3 H3-1井储层综合分析图

裂缝参数预测结果/m监测结果/m相对误差/%符合率/%半缝长257.62251585缝高91.9100892
根据上述方法,分析得到起裂压力、起裂角以及在最大泵压95.0 MPa条件下预测的压裂裂缝长度、垂向延伸最大距离:起裂压力96.44 MPa;起裂角36.7°;裂缝半缝长2 576 m;裂缝高度91.9 m。预测的压裂裂缝形态(以破裂扩展点表示)见图4。
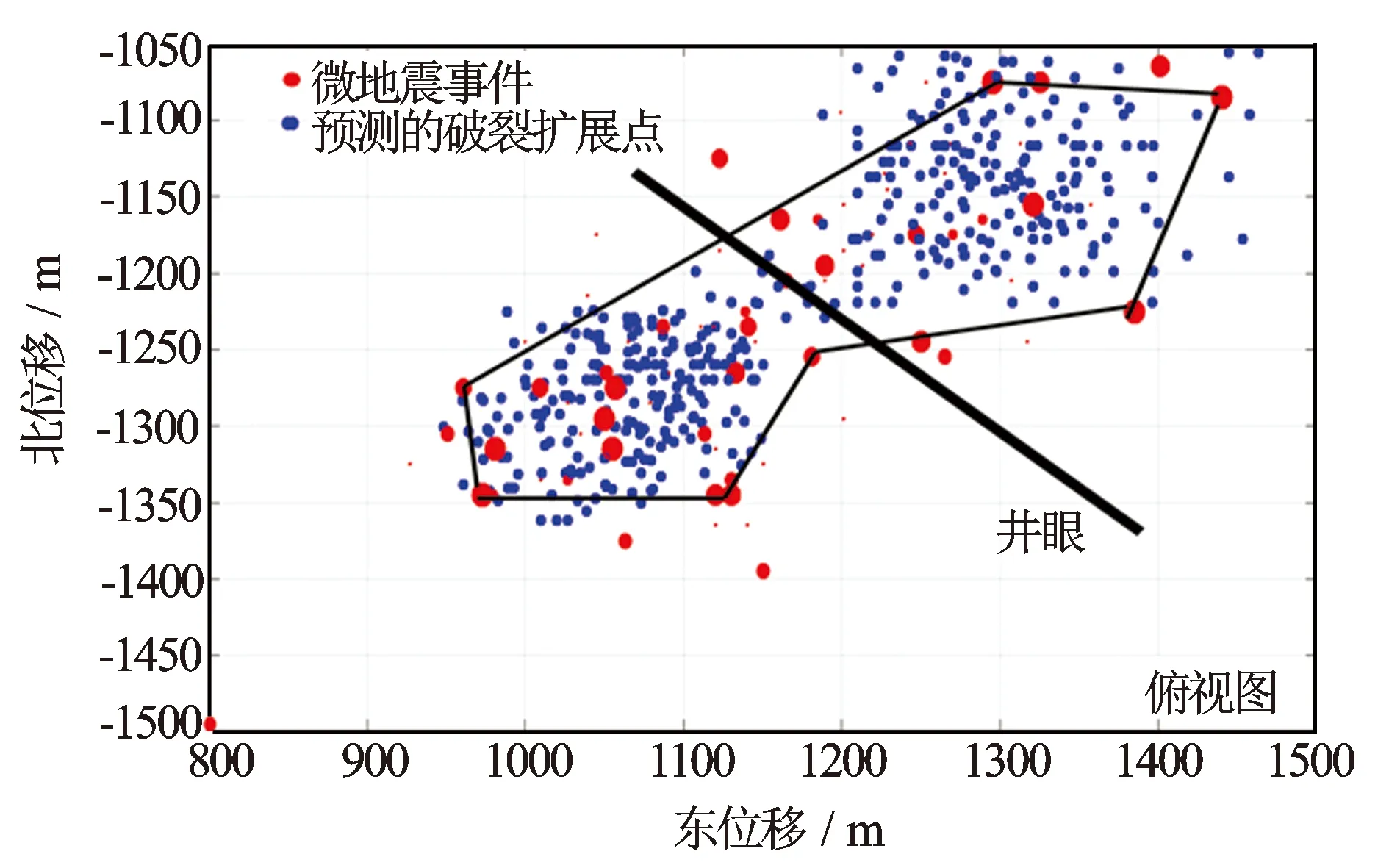
图4 H1-3井预测的裂缝形态与微地震事件重叠图
H1-3井进行了微地震压裂监测,监测结果表明,H1-3井第1压裂段裂缝半缝长225 m,裂缝高度100 m。将上述H1-3井预测的裂缝半缝长和裂缝高度与微地震监测结果进行对比,结果表明符合率平均为89%。为了更直观地对比,将H1-3井预测的裂缝形态与微地震事件分布图重叠(见图4),重叠图表明模拟结果能够反映近井周围压裂裂缝的延伸情况,效果较好。
4 结 论
(1) 通过研究四川页岩气水平井岩石力学、裂缝起裂和延伸数学模型,建立了用测井资料预测水平井压裂裂缝形态的方法。
(2) 裂缝延伸模型中考虑了井周裂缝应力、流体状态对应力强度因子的实际作用,可用于研究水平井筒任意方位下压裂裂缝的延伸规律。
(3) 预测的压裂裂缝形态与微地震监测结果的对比表明模拟结果能够反映近井周围压裂裂缝的延伸情况。
参考文献:
[1] 江万哲, 章成广, 黄文新. 用测井资料预测压裂裂缝高度的方法研究 [J]. 测井技术, 2007, 31(5): 479-481.
[2] 齐宝权, 谢刚, 张树东, 等. 地层破裂压力测井解释技术在LG地区的应用 [J]. 天然气工业, 2009, 29(10): 38-41.
[3] 张广清, 陈勉. 水平井水力裂缝非平面扩展研究 [J]. 石油学报, 2005, 26(3): 95-97.
[4] 李兆敏, 蔡文斌, 张琪, 等. 水平井压裂裂缝起裂及裂缝延伸规律研究 [J]. 西安石油大学学报(自然科学), 2008, 23(5), 46-48, 52.
[5] 程远方, 王桂华, 王瑞和. 水平井水力压裂增产技术中的岩石力学问题 [J]. 岩石力学与工程学报, 2004, 23(14): 24632466.
[6] HOSSAIN M M, RAHMAN M K, RAHMAN S S. Hydraulic Fracture Initiation and Propagation: Roles of Wellbore Trajectory, Perforation and Stress Regimes [J]. Journal of Petroleum Science and Engineering, 2000, 27(3/4): 129-149.
[7] TALEGHANI A D. Fracture-initiation as a Possible Branching Mechanism During Hydraulic Fracturing [C]∥ARMA 10-78, 2010: l-7.
[8] OLSON J E. Multi-fracture Propagation Modeling: Applications to Hydraulic Fracturing in Shales and Tight Gas Sands [C]∥ARMA 08-327, 2008: 1-8.
[9] WENG X, KRESSE O, COHEN C. Modeling of Hydraulic Fracture Network Propagation in a Naturally Fractured Formation [J]. SPE Production & Operations, 2011, 26(4): 368-380.
[10] KRESSE O, WENG X W, GU H R, et al. Numerical Modeling of Hydraulic Fractures Interaction in Complex Naturally Fractured Formations [J]. Rock Mechanics and Rock Engineering, 2013, 46(3): 555-568.
[11] 赵金洲, 李勇明, 王松, 等. 天然裂缝影响下的复杂压裂裂缝网络模拟 [J]. 天然气工业, 2014, 34(1): 68-73.
[12] 刘振宇, 刘洋, 贺丽艳. 人工压裂水平井研究综述 [J]. 大庆石油学院学报, 2002, 26(4): 96-99.
[13] 米卡尔·J·埃克诺米德斯, 诺尔特著. 油藏增产措施 [M]. 3版. 张保平, 蒋阗, 刘立云, 等译. 北京: 石油工业出版社, 2002.
[14] 郭建春, 苟波, 任山, 等. 川西页岩砂岩交互水平井压裂参数优化设计 [J]. 石油学报, 2014, 35(3): 511-518.
[15] 李金柱, 李双林. 岩石力学参数的计算及应用测井技术 [J]. 测井技术, 2003, 27(增刊): 15-18.
[16] 刘景武. 硬地层中用多极子阵列声波资料计算力学参数及识别裂缝 [J]. 测井技术, 2005, 29(2): 137-140.
[17] 杨小兵, 杨争发, 谢冰, 等. 页岩气储层测井解释评价技术 [J]. 天然气工业, 2012, 32(9): 33-36.
[18] 杨小兵, 张树东, 钟林, 等. 复杂多矿物组分的页岩气储层横波时差预测方法 [J]. 天然气工业, 2015, 35(3): 36-41.
[19] 陈建国, 邓金根, 袁俊亮, 等. 页岩储层I型和II型断裂韧性评价方法研究 [J]. 岩石力学与工程学报, 2015, 34(6): 1101-1105.
[20] 谢刚. 用测井资料计算最小和最大水平应力剖面的新方法 [J]. 测井技术, 2005, 29(1): 82-89.
[21] HOSSAIN M M, RAHMAN M K, RAHMAN S S. A Comprehensive Monograph for Hydraulic Fracture Initiation from Deviated Wellbores Under Arbitrary Stress Regimes [C]∥Paper54360-MS Presented at the SPE Asia Pacific Oiland Gas Conference and Exhibition, 20-22 April1999, Jakarta, Indonesia. NewYork: SPE, 1999.
[22] 郭天魁, 张士诚, 刘卫来, 等. 页岩储层射孔水平井分段压裂的起裂压力 [J]. 天然气工业, 2013, 33(12): 87-93.
[23] IRWIN G R. Analysis of Stresses and Strain Near the End of a Crack Traversing a Plate [J]. J.APP. Mech, 1956, 24(3): 361-364.
[24] 江万哲, 章程广, 黄文新. 用测井资料预测压裂裂缝高度的方法研究 [J]. 测井技术, 2007, 31(5): 479-481.
[25] 胡南. 苏里格气田二叠系储层水力压裂缝长宽高的测井预测 [D]. 成都: 西南石油大学, 2012.

