借助“问题串”，发展学生的思维能力

江苏省南通大学附属中学(226000)

李带兵●



借助“问题串”，发展学生的思维能力

江苏省南通大学附属中学(226000)

李带兵●

在高中数学教学过程当中，问题的巧妙串连关系到整个教学活动能否高效顺畅地进行.作者立足基本教学理论，对“问题串”的设计方法进行了讨论与阐述，希望能够起到抛砖引玉的作用，对广大高中数学教师们形成启发.

高中；数学；问题串

“问题串”是高中数学教学当中十分常用的一种设计方法.它的核心在于将教学过程中所涉及到的问题按照一定逻辑顺序进行处理和排列，将它们科学地串连起来，让一个个独立的问题以问题串的形式出现，带来更为可观的教学效果.这是在传统教学基础上的继续深化与创新，对既有教学资源实现了整合，使得数学教学进展得更加顺畅高效.

一、关注“问题串”的出现时间，发挥应有教学作用

在高中数学教学过程当中，虽然各类问题出现得颇为频繁，但“问题串”却不是随时都适合适用的.如果在不适宜的时间强行运用“问题串”进行教学，不仅无法优化数学教学效果，反而会造成时间与精力的过度消耗，让学生们的学习热情减退，产生教学促进的反效果.

例如，在立体几何的教学过程当中，我在完成了基础知识的教学之后，向学生们提出了这样一串问题：已知ABC-A1B1C1是一个直三棱柱，且它的所有棱长均为2，点D是棱CC1的中点.(1)求证：直线AB1与平面A1BD相垂直；(2)能否求出二面角A-A1D-B的正弦值？表面看来，这两个问题都是围绕十分基础的知识内容所提出的，但真正解答起来便会发现，想要将它们快速准确地解答出来也并不是那么容易的.线面垂直与二面角的内容，其灵活程度是很高的.如果学生们仅仅是从文字概念的角度对之进行学习，难免会将知识掌握得过于书本化.而到了具体图形的分析当中，就不知道该如何寻找线面关系和确定二面角的位置了.由此可见，教师们所设计的“问题串”，不能在基础知识的呈现过程当中贸然引用.要在学生们将基本的概念与方法理解得较为到位之后，再对“问题串”加以思考，方能发挥出其应有的效果.

想要将“问题串”适用于最为适宜的教学时间，教师们首先要对这种教学设计的目的有一个到位的认知.我们之所以要把一个个数学问题串连起来，就是要以长线过程的方式将学生们的思维逐步深化.因此，只有当学生们对于基础知识已经具备了比较全的把握之后，“问题串”的出现才是有意义的.

二、关注“问题串”的组成结构，形成明确思维梯度

高中数学教学过程中的“问题串”，并不是单个问题的简单堆积，而是要将甄选出的问题按照一定的逻辑关系加以串连的，为的是对学生们的知识思维形成科学引导.因此，具体怎样来串连这些问题，应当让它们以什么样的结构呈现出来，就成为了教师们必须重视的课题.

例如，在对数列的内容进行教学时，为了逐步深化学生们对于相应知识的理解，我特意在课堂上引入了这样一个串连式问题：已知{an}是一个等差数列，它的前n项和是Sn，且a1的值为2，a3的值为6.(1)数列{an}的通项公式是什么？(2)如果Sk的值是110，那么，k的值是多少？(3)如果数列{Sn}的前n项和是Tn，那么，T2013的值是多少？在这个“问题串”中，第一个问题是从最基本的通项公式角度提出的，求解难度也是最低的.到了第二个问题，加入了等差数列前n项和的内容，并包含了逆向思维的元素，思考难度也就随之增加了一些.进入到第三个问题中，继续从当前数列延伸，构造出一个新的数列，思考难度达到了最大值.随着问题难度的逐级递增，一个鲜明的思维阶梯就此形成.在这样的阶梯辅助之下，学生们对于数列知识的认知也实现了一个新高度.

一般来讲，“问题串”应当是按照由浅入深的结构来进行设计的.为学生们预先设置好思维的起点和终点，大家便可以在一个个问题的连续引导之下，于准确的轨道上逐步深化自己对于当前知识内容的理解了.

三、关注“问题串”的设计尺度，收放自如强化能力

除了从形式的角度来思考“问题串”的设计方法之外，教师们还应当从内容的角度来对之来加以关注.为了能够最大限度地拓展“问题串”的适用价值，我们有必要在串连问题的过程中兼顾基础内容与开放内容，让整个“问题串”呈现出收放自如的样态，将高中数学教学的实效推上一个新高度.

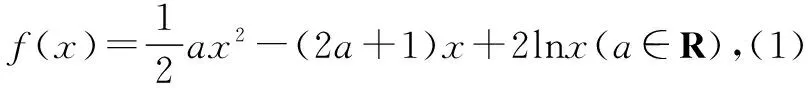
同时具备基础性问题与开放性问题的“问题串”，显然具备了更加广泛教学应用价值.通过这种教学模式的适用，很顺利地同时完成了对学生知识细节的夯实以及思维能力的升华.借助“问题串”进行教学，很好地实现了教学效率的提升.

根据教学内容与教学要求的不同，将数学问题进行串连的方法和方向也是有所不同的.通过前文当中的叙述不难发现，“问题串”在高中数学教学当中的构建模式是灵活多变的.经过这种串连式的处理，学生们的思维过程被有效延长了.这也为大家提供了一个数学学习上的启发，特别是在面对比较复杂的知识内容时，尽量将思维拓展拉伸，往往能够收获更加深入到位的探究效果.

G632

B

1008-0333(2017)12-0018-01