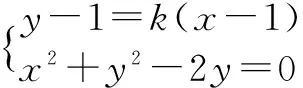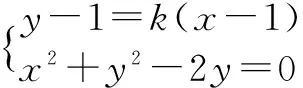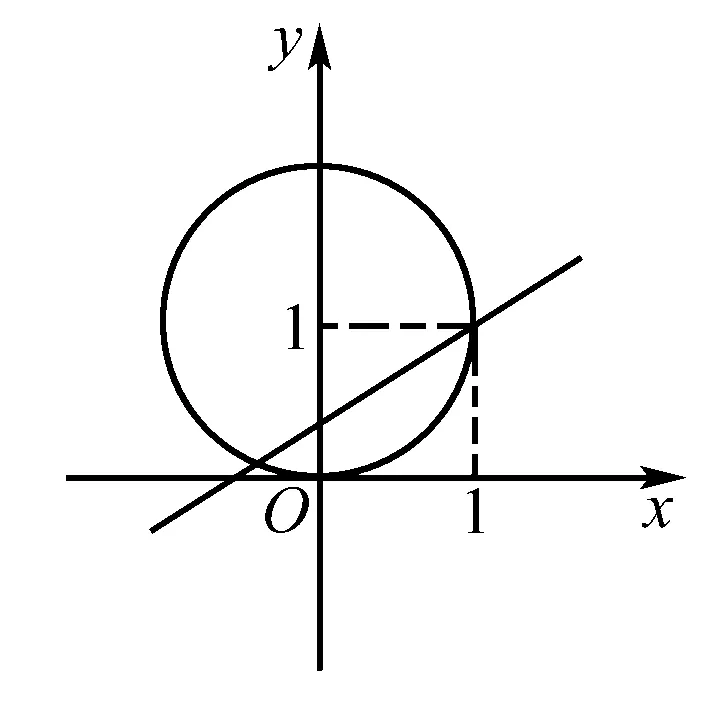谈创新素质与创新思维的培养

甘肃省景泰县第一中学(744000)

高兴霞●



谈创新素质与创新思维的培养

甘肃省景泰县第一中学(744000)

高兴霞●

本文在回顾与启发中重点叙述什么是创造思维怎样产生创造思维,创造力与创造思维的关系，本文第二部分通过实践过程培养创造思维过程.

创新素质；创造力与创造思维关系；数学解题

一、回顾与启发

从古至今，人的想法和理念成就了自然科学和社会科学领域的许多重大发明：在远古时期，当欧洲大陆还在沉睡时，东方的先哲们就开始对自然、宇宙和人生进行思索和实践，并形成了一系列朴素的价值观，直到今天还在泽被着一代代的后人，指南针的发明缩短了世界各国的距离，印刷术的发明便利了文化的传播…在近现代，爱因斯坦创造性地提出了相对论的有关理论，将人类的视野从三维世界向更多维空间扩展，内燃机的发明使石油变成了一种非常有价值的资源，硅片的发明使世界上最普通的砂子改变了众多人的生活方式…无怪乎美国的乔治·布什总统不无感慨道：“我们不要忘记，不是政府使美国强大起来，使美国强大起来的是富有想象力的人和使他的梦想得以实现的方法.”

中华民族自古就是一个非常有智慧的民族，“2000多年前，中国就出现了诸子百家的盛况，老子、孔子、墨子等思想家上究天文、下穷地理，广泛探讨人与人、人与社会以及人与自然关系的真谛，提出了博大精深的思想体系.他们提出的很多理念，如孝悌忠信、礼义廉耻、仁者爱人、与人为善、天人合一、道法自然、自强不息等，至今仍然深深影响着中国人的生活.”坦普尔在《中国：发明和发现的国度》一书中曾经提到：现代世界赖以建立的基本发明创造，一半以上源于中国.中国在现代农业、航运、石油、气象、音乐、十进制数学、纸币、高级火箭、枪炮、载人飞机、蒸汽机设计等领域创造了100个世界第一…古中国有四大发明，有都江堰、赵州桥、北京故宫等伟大的工程，现在看来都可称作科技创新的项目.

什么是创新素质？我们很难用一句话简单概括，因为它是一种综合素质，但是纵观科学、艺术和技术发展，它们的共同基础都是宇宙的替身规则和人类的想象力、创造力，两者缺一不可.

艺术，例如诗歌、绘画、音乐等，是创作者将对生命、宇宙、人生的感情通过艺术形式的表现唤起人们的意识或潜意识中深藏着的已经存在的情感；自然科学，例如化学、物理、生物等是用数学公式或自然定律的方式对自然界的现象进行准确的抽象，虽然自然现象是不依赖于科学家的主观意志而存在的，但这种抽象的过程和艺术家的创造是一样的；发明则更是依靠发明家的经验和创造性活动进行技术革新.可以说古往今来，所有被称作天才、人才、通才、伟才的科学家、文学家都具有出色的创造力，创造力是构成创新素质的最主要组成部分.

科学家对机器的大胆设想，是从现实需要出发，作家和家对人物的逆造也是从现实生活中取材的.人们把实践活动和观察社会中获得的表象进行艺术加工，创造出新形象的过程就是进行创造性思维的过程.

生活经历不同，观察事物的角度不同，每个人的想象也不同，例如：新疆游客看到云南石林，可能会把它想象为一个个戴着维吾尔族小花帽的石人；内蒙古游客看到石林，会把它想象为一把把锋利的马刀；渔民看见石林，会把它想象为创耸立的桅杆；林业工人看见石林，则把它想象为无边的林海.石林“变”为戴花帽的维吾尔人、蒙马刀、桅杆或林海是和每个游客的阅历血肉相连的.想象源于生活又高于生活，观察、经历越丰富，想象也越丰富，观察和阅历的想象储备了丰富的表象.

人的大脑是一个非常复杂的物质器官，它不仅有记忆、联想的功能，还有学习的功能，人在一生中的经历是有限的，但是知识的获取是无限的.古往今来，人们在生产劳动、生活实践中积累的经验，在朝代更迭中总结的教训为我们开拓了广阔的时空，为我们提供了丰富的表象素材.

在创造性思维中有两种思维方式格外引人注目，它们就是灵感和直觉，这两种思维方式的产生有多种提法，关乎人体科学和另外时空的研究，但是它们的产生往往需要创造者坚持不懈的探索，有时这种探索到了“山重水复疑无路”时，“柳暗花明又一村”，而出现转机.当然不是所有的持之以恒都能使思考结出创新的果实，但是许多伟大的发明确实来自于发明者持之以恒的坚持.

二、培养创造思维的实践过程

怎么才能将已经学到的知识灵活用于解题？这就是“解题思维过程”.

在数学中，形象思维与逻辑思维不是互相独立的，而是密不可分的，反映在解题方法上，我们最常鼓励学生使用“数形结合法”，因为它既快捷又直观.而熟练的解题方法来源于对知识点的熟练掌握，学生只要对数学概念有较深的理解，就会自然地将其融入解题方法、用于思维过程里.一味地单独强调“培养思维”而忽视对基本概念的深入理解，是不可能凭空在学生脑内构造出真正的思维模式的，也不可能培养出真正的数学思维能力.下面通过《集合简易逻辑》的一个解题实例总结培养创造思维过程.

例题一 设全集U=R，集合A={x|x2-4x+3≤0},集合B={x|x2-(a+1)x+a<0}.

若B⊆A，则实数a的取值范围是____.

分析与思考 集合A中的元素是由不等式x2-4x+3≤0的解为1≤x≤3，而不等式x2-(a+1)x+a<0对应的方程x2-(a+1)x+a=0的两根分别为1和a，需讨论a<1,a=1,a>1,三种情况.从而确定集合B，就可以求出实数a的范围.

解法一 解不等式x2-4x+3≤0得集合A={x|1≤x≤3},又方程x2-(a+1)x+a=0的解为x=1或x=a.

当a<1时，B={x|a

当a=1时，B=Φ，满足B⊆A;

当a>1时，B={x|1

综上所述，1≤a≤3.

解法二 解不等式x2-4x+3≤0得集合A=[1,3],由x2-(a+1)x+a<0可知集合B的区间为(x1,x2),此时x1

评论 解法一用到了分类讨论，有的同学不知道在什么情况下需要分类讨论，如何分类.就此题而言，A、B都是区间，A可以写为[1,3]，而B是写成(a,1)还是写成(1,a)，要比较a与1的大小才能确定，这就得分三种情况考虑a，这就是分类讨论.由a∈R，故a可能比1大，也可能比1小，或者等于1.只有这三种情况，这就是如何分类.

解法二实际上是数形结合法，解出不等式，画出集合A的区间，集合B在数轴上有两个位置(空集除外)一看便知.

例题二 已知集合M={(x,y)|y-1=k(x-1),x,y∈R},集合N={(x,y)|x2+y2-2x=0,x,y∈R},那么M∩N中( ).

A.不可能有两个个元素 B.最多有一个元素

C.不可能只有一个元素 D.必含有无数个元素

将直线方程代入圆的方程，得到一个关于x的一元二次方程，由其判别式的情况可知方程的根的个数，从而M∩N中元素的个数可定.当然，也可以利用数形结合法，这种方法更简捷.

由于1+k2≠0，且Δ=(-2k2)2-4(1+k2)(k2-1)=4>0可知，方程(1)有两个不同实根，从而M∩N中必有两个元素.故选C.

图1

解法二 如图，集合M是过点的一条直线，集合N是圆心为(0，1)，半径为1的圆，如图1所示，因为直线的斜率存在，故直线与圆必有两个交点.故选C.

评论 解法一是代数法，直接从描述集合元素的方程入手，解方程组考察方程解的个数.解法二是数形结合法，由两个集合所对应的图形直接观察交点的个数，即M∩N中元素个数.对于本题来说，宜用数形结合法.

[1]章慧蓉，郭文，杨静编写.《开启创新之门》冶金工业出版社出版.

[2]黄东坡著.《数学培优新方法》湖北人民出版社出版.

G632

B

1008-0333(2017)12-0003-02