转化数学语言对学生解题思维的活化作用

福建省永安市第一中学(366000)

江 冰●



转化数学语言对学生解题思维的活化作用

福建省永安市第一中学(366000)

江 冰●

本文阐述了数学语言的特征以及通过转化数学语言解决数学问题的思路和方法,以培养学生的思维能力.

数学语言;转化;数学思维

一、数学思维的特点

解决数学问题就是一个不断的提出设想，验证设想，修正和发展设想的过程.这就要求有一定的数学能力.数学能力主要体现在抽象概括能力、推理能力、逻辑推理能力、选择判断能力和数学探索能力.数学解题思维能力是我们的大脑对数学本质属性的把握，学习规律、探求数学结论，探索解题途径，寻找解题方法，概括数学规律，对数学材料进行加工整理的活动过程.数学解题思维能力是表现学生数学能力的核心，直接影响着学生的数学成绩及发展.数学解题思维能力能够分离出问题的核心，把本质的与非本质的东西区分开来，从非本质的细节中使自己摆脱出来，能够将数学材料中反映的数与形的关系从具体的材料中抽象出来，善于把具体问题抽象为数学模型.

二、数学语言的组成和特征

数学语言分为文字语言，符号语言和图形语言三种.文字语言主要是指人们通常所说的自然语言，用语文语言来表述数学问题及空间关系.符号语言就是指在数学中的各种数字及符号.图形语言就是数学中的各种图象，图形和图表.他们共同组成了数学语言，但是他们之间各有利弊，文字语言通俗易懂，概括性强但不够抽象，简洁，符号语言简洁精确，能够准确的表达数学知识，体现数学的高度抽象性，但太过抽象，不易理解.图形语言比较直观，易懂，但不利于数学推理，又不利于叙述.

三、转化数学语言，解决数学问题

数学语言的转化是指不改变数学本身的意思，及所表达的本质内容，而是在表达形式上让三者之间相互转换或相互结合来表达数学本意.在这三种数学语言转换的过程中最要注意的是把握问题的实质.

1.数学里面有许多公式和概念，都可以用这三种数学语言进行描述

比如在高中数学中学到的交集、并集，补集，就可以用这三种语言表述.他们三者之间只是表述不一样但是要表达的数学本质是一样的.

现在以其中的交集为例：

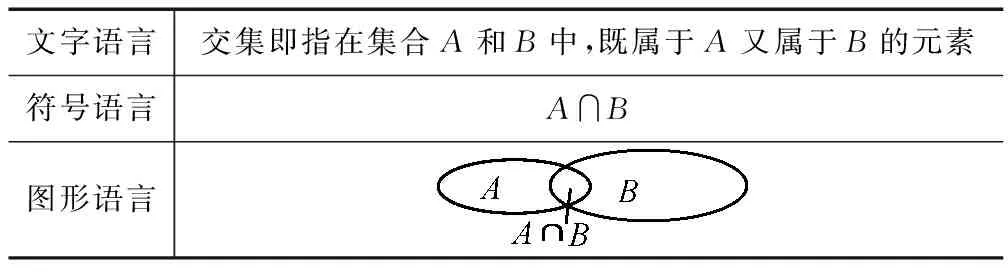
文字语言交集即指在集合A和B中,既属于A又属于B的元素符号语言A∩B图形语言

2.“以形助数，以数解形”

例1 有48名学生，每人至少参加一个活动小组，参加数理化的小组的人数分别是28,25,15，同时参加数理小组的8人，同时参加数化小组的6人，同时参加理化小组的7人，问同时参加数理化小组有多少人？

分析 可以用A,B,C分别表示参加数理化小组的人数，三个圆的公共部分是表示参加数理化小组人数.

根据上面图形可列公式：

A+B+C-A∩B-A∩C-B∩C+A∩B∩C=48,

28+25+15-8-6-7+A∩B∩C=48,

∴A∩B∩C=1.∴同时参加数理化小组的有1人.

用图形结合解决三角函数问题.

例2f(x)=sinx+2sinx,x∈[0,2π]的图象与直线y=k有且仅有2个不同的交点，求k的取值范围.

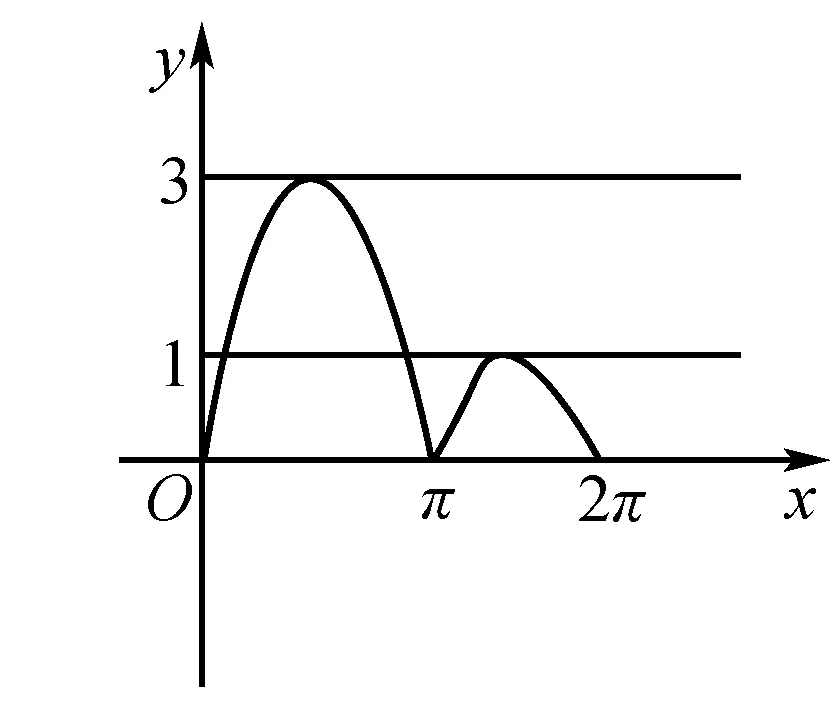
解题思路 根据函数解析式，画出图象，直观而简明的知道答案.

f(f)={3sinx,

-sinx,x∈[0,π],

x∈[π,2π].由图象可知：1

四、总结数学语言转化对数学解题思维的作用

1.转换让数学对象变得更加丰富

三种数学语言之间互有利弊，各有所长，相得益彰.文字描述，数形结合，以形助数，以数解形.例如数形结合，可以解决函数与图象的关系，曲线与方程的关系，以及几何代数问题等.三者之间的转换、结合有利于学生找到解决问题方向，快速解决，并且能够让学生对一个问题，有更多不同面的解决方法，加深对问题的理解.

2.说数学，读数学，把握数学的本质，更好地解决数学问题

文字语言是基础，首先要能读懂题干问题，才能进一步知道问题所在，关键知识的运用.文字概括性强，文字语言能够更好地把数学所要表达的意思说出来.学数学也是说数学，读数学的一个过程.数学不是一成不变的符号，可以表现形式不同，但其呈现着自身内在的规律，问题实质不会发生变化.一个问题可以有多种不同的解决办法，通过用不同的数学语言来呈现，有利于让学生把不是特别熟练的数学特征转化为自己比较容易接受理解的表现形式，有利于解决问题.

3.增加学生对数学的理解程度，因材施教，提高教学效率

每个学生的学习能力不一样，导致接受能力也自然会不一样.同样的一个数学题目，老师如果用三种不同的数学语言把它表述出来，这对不同的理解能力的学生会有不一样的影响，有的对文字比较敏感，能够准确把握文字的意思，而有的会对公式比较感兴趣，喜欢推导验算，有的空间想象能力比较强，喜欢把文字、符号转化为图形.所以采用多种不同的表述方式，让学生有选择性地体会其中一种，加深理解，把握对象的本质，更好地学好数学.

G632

B

1008-0333(2017)12-0017-01