有所侧重更有效——高三数学复习教学的几点思考

江苏省通州高级中学(226300)

袁 源●



有所侧重更有效
——高三数学复习教学的几点思考

江苏省通州高级中学(226300)

袁 源●

高考的成败受高三复习课有效与否的直接影响，高三复习课不仅仅涵盖高一、高二所学知识点的回顾，更重要的是对数学思想方法的提炼、数学模型的建立、关联知识的整合，因此，在高三复习的整个过程，教师与学生都要做到“三思而后行”，把复习的侧重点、例题的选择、习题的讲评列入复习课的考虑范围.

高三数学；例题；讲评；通性通法

高三的复习在整个高中数学学习阶段自然是非常重要的，借助复习资料——学生练——教师讲的传统模式对于高三数学复习的有效性是缺乏思考环节的，更加不谈该复习资料的选择对于全体学生的发展是否确实有针对性了.新课程与传统教学模式相比根本性的差别就是学生地位的改变，因此，高三复习课中教师仍然要谨记学生主体这一根本性原则，客观评价学生具体的学习情况，分析学生高中数学整个知识体系的掌握情况，切合实际地制定复习的计划、准确把握复习的侧重点，使得整个复习阶段更加系统和全面.具体说来，教师要基于学生最近发展区科学选择适合学生的例题，使得各个知识成分的有机整合借助例题能够实现，继而再从学生对于例题的把握情况出发，与学生一起评价、分析、讨论、反思数学概念以及解题的思路和方法，在帮助学生打牢基础的同时，促进学生分析解决实际问题能力的提高.

一、有所侧重

高考的指导思想和方针是坚持全面考查和突出重点相结合.从近年来的高考试卷分析来看，高考考查的知识面广但重点突出，“题在书外、根在书中、淡中见隽”是高考试题的整体特征.所以高三数学复习课应该紧紧围绕这一思想抓住复习的侧重点，把握高中数学学科知识的主干以及主干内容中学生学习情况不够好的地方.比如集合与函数、三角函数与平面向量、数列、不等式、立体几何、概率与统计、排列、组合、二项式定理等都是高三复习中应该重点关注的，教师还应把新旧教材以及课标要求的差异处理好，并在知识和模型的基础上注重数学思想方法的渗透，整个高三数学的复习也就比较完整了.

高考命题倡导的基本理念还有“通性通法”.分析历年的高考试题，我们可以看出对于通性通法的考查、对解题能力与思维水平的考查都涵盖其中.原创化构思、通俗化叙述、大众化解题是这些试题的外在表现，这些试题在通法、基础和能力方面都进行了深入的挖掘，解题都有多种不同的方法，但是采用常规的解题方法与通性通法也都能得出正确的答案，不过完整而又正确的答案还是需要扎实的数学功底的.当然，如果学生具有一定的数学直觉和解题智慧并且能将特殊方法进行应用的话，解题便会变得更加简捷准确了.具有一定难度的题目往往需要通性通法和巧妙解法相互融合才能圆满解决的，因此，高三复习课中我们狠抓双基训练的同时还应该强调学生巧妙应用通性通法.

二、精选例题

例题是知识传输的载体，实现数学复习课堂高效的前提必然是精选的例题.因此，新颖性、层次性、过程性、关联度应该是一个精选的例题同时具备的，并在此基础上留足时空给学生自主深入地思考.比如，师生共同复习“直线和圆锥曲线的位置关系”时有这样一题：

例1A和B是直线l：y=2x+m和抛物线：y=x2相交的两个点，请同学们自主尝试添加一个能够得出直线l方程的条件.

这道例题为学生创造了较大的思维空间，促动了不同学生的思考，得到了不同的答案反馈，使得相关数学知识方法均得到了应用，把知识与能力的锻炼有机地融合到了一起.

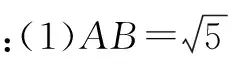
三、质性讲评

高三复习最关键的教学环节是习题的讲评，传统教学中一讲到底的现象比较多，其实，讲解习题时教师首先应该选择必须讲的内容且注重习题讲解的实效性，使学生的思维得以流露.

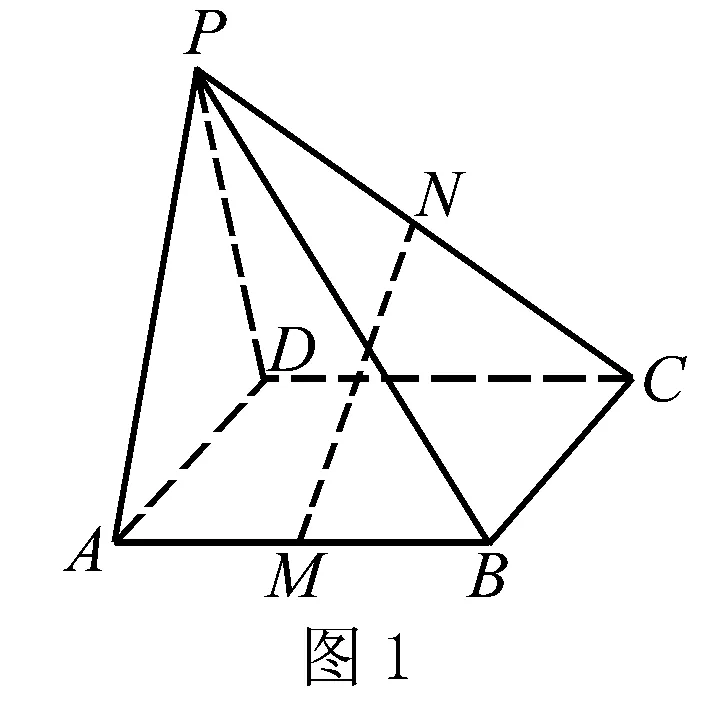
例2 观察图1，P-ABCD是四棱锥，矩形ABCD为其底面，AB的中点为M，PC的中点为N，请证明MN∥平面PAD.

例题给出以后，笔者主动观察巡视学生的思考探索，发现学生主要有两个解题思路：(1)由面∥面到线∥面的推理论证；(2)线∥线到面∥面的直接推理论证，采用这个思路的学生不多，主要是遗漏附带条件的现象较严重.

笔者把这些错误呈现到学生面前，让学生自主讨论与思考.面对第二种思路，笔者注重引导学生互动探究找出问题的难点，激活学生思维的同时也巩固了知识.

最后笔者跟学生一起对该题进行了反思，把论证平面与平面平行的方法及推理过程中相关的转化思想进行了总结.这个环节很多教师容易遗漏但非常重要，这是一个运用相关知识有效回顾思想方法和策略的过程，是学生内化知识最为关键的环节，是学生能力提升的显现.

因此，高三复习课同样是体现学生主动发展的实践活动，在注重基础知识、技能、通性通法的同时教师把控好例题的精选，使得学生在解题时熟练运用自身的知识经验，增强数学综合能力，有效提高数学成绩.

G632

B

1008-0333(2017)12-0005-01