基于T-S模型的随机切换模糊系统的稳定性研究

张 乐, 郭春鹏, 关 忱, 李 智, 杨 红

(沈阳大学 信息工程学院, 辽宁 沈阳 110044)



基于T-S模型的随机切换模糊系统的稳定性研究

张 乐, 郭春鹏, 关 忱, 李 智, 杨 红

(沈阳大学 信息工程学院, 辽宁 沈阳 110044)

通过切换技术研究了一类基于T-S模型的不确定随机切换模糊系统均方镇定问题.基于多Lyapunov函数和线性矩阵不等式(LMI)设计随机切换模糊系统状态反馈控制器,给出稳定性条件及相应的使得系统镇定的切换律设计方案.随机切换模糊模型中的每个切换子系统是随机模糊系统,当某些子系统不稳定时,构造恰当的切换控制策略,可以使整个随机切换模糊系统稳定.通过仿真实验验证了该设计方法的可行性及有效性.

随机; 切换; 模糊; 均方稳定; 切换律

在实际系统中,由于控制过程的复杂性、外部扰动和系统的一些限制,非线性,不确定性,延时等是广泛存在的.最近,切换系统作为一类重要的混杂系统得到了越来越多学者的重视[1-5].这不仅解决了复杂系统控制上的难题,也使得控制过程相比传统自适应控制算法更简单、易实现.T-S模糊系统通过模糊规则给出非线性系统的局部线性表示,它可以逼近很大一类非线性系统.目前,基于Lyapunov稳定性理论,对系统的稳定性和性能指标等进行理论分析,研究模糊控制系统的稳定性分析和鲁棒控制等已经成为模糊控制领域中最重要的研究方向之一[6-9].与此同时,基于T-S模糊模型的模糊切换控制也逐渐成为专家研究的重点[10-12].2006年我们中提出了复杂组合的切换模糊系统[13]与文献[10-12]所研究的switching fuzzy systems不同,该模型突破目前采用的两级结构,将T-S模糊模型建立为切换系统的子系统,即子模糊模型,其是一类更一般的系统.

随机系统是指含有内部随机参数、外部随机干扰和观测噪声等随机变量的系统.各种电子装置中的噪声,生产过程中的种种随机波动等,都是随机干扰和随机变量的典型例子.基于切换模糊系统和随机系统的现有成果,本文研究一类不确定随机切换模糊系统的均方稳定问题.随机切换模糊系统是集合了随机控制、模糊控制以及切换控制相互作用关系的一种耦合控制系统.这类系统则更能准确刻化实际系统中模糊特性、连续动态和离散动态的相互作用及运行行为.同切换模糊控制系统方面的成果相比,关于随机切换模糊系统的问题的研究结果尚相当有限.我们利用多Lyapunov函数方法,设计状态反馈控制器,给出切换规则的组合形式,并研究系统均方稳定的充要条件.

1 问题描述

含有Nσ(t)个模糊规则的随机切换模糊系统模型为

(1)

其中,

(2)

则第i个随机切换模糊系统的数学模型为:

因此,第i个随机切换模糊系统的全局数学模型为

(4)

其中,

(5)

有

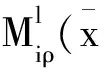
考虑借鉴模糊系统中的平行分布补偿(parallel distributed compensation,PDC)控制器,这里取与系统(1)相同的前件变量,设计切换PDC控制器,即

(6)

则控制器(6)的全局模型为

(7)

第i个随机切换模糊系统的闭环全局数学模型可描述为:

(8)

假设:参数不确定项是范数有界的,并且满足下列不等式

(9)

(10)

系统切换信号设计为:

(11)

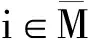
(12)

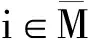
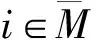
注意到,如果式(12)成立,则

(13)

(14)

其中,Pi为正定对称矩阵.

那么

(15)

考虑式(13),可以得到

所以

(17)

那么

(18)

对式(18)两边从ta到tb积分,接着取数学期望,经计算可得

(19)

进而,式(21)可以写成

综上所述,随机切换模糊系统(1)是均方稳定的.

下面给出式(10)的依赖于线性矩阵不等式的可行解.

(20)

其中,

系统切换信号设计为:

(21)

2 仿真实例

Lorenz系统是一类典型的混沌系统,具有强烈的初值依赖性和长期不可预测性.为了建构子系统足够多又能容易相互切换的混沌系统,文献[14]采用增加并改变系统非线性特性的方法,通过系统选择器的切换,设计了能实现多个关联功能的电路.

为了电路实现时能满足运算放大器和模拟乘法器对输入电压限制的要求, 将这类混沌系统方程表述为以下形式:

这类系统是相互关联的并且可以相互切换,这种关联性不仅为系统的电路实现带来了方便,而且系统具有一定的实际应用价值.

其中

令β11=0.5,β12=0.6,β21=0.4,β22=0.8和λ1=λ2=1.求解LMIs(20),可以得到

取初始条件x(0)=[-1;4;-1],图1～图3描述了MATLAB仿真结果.图1为随机切换模糊系统的状态曲线,图2～图3为随机切换模糊系统的子系统1和子系统2的状态曲线.从仿真结果可以看出,当子系统1和子系统2的收敛效果都不理想时,通过设计切换信号可使随机切换模糊系统状态达到良好的性能.

图1 随机切换模糊系统的状态响应曲线

图2 随机切换模糊子系统1的状态响应曲线

图3 随机切换模糊子系统2的状态响应曲线

3 结 论

本文研究了不确定随机切换模糊系统的控制问题.首先,提出一类随机切换模糊系统模型,其蕴含了随机控制和切换模糊控制的优势.同时,随机切换模糊系统的所有子系统为随机模糊系统.基于多Lyapunov函数,提出一种新的稳定性.通过设计切换策略,稳定性条件以可解的LMI形式给出.最后,对比的仿真例子验证了所提出方法的可行性和有效性.

[ 1 ] SUN X M, LIU G P, WANG W, et al. L 2-gain of systems with input delay and controller failure: zero-order hold model[C]∥Proceedings of the 2010 American Control Conference, 2010,19(3):4058-4063.

[ 2 ] WU L, FENG Z, ZHENG W X. Exponential stability analysis for delayed neural networks with switching parameters: average dwell time approach[J]. IEEE Transactions on Neural Networks, 2010,21(9):1396-1407.

[ 3 ] ALI M S.On exponential stability of neutral delay differential system with nonlinear uncertainties[J]. Communications in Nonlinear Science and Numerical Simulation, 2012,17(6):2595-2601.

[ 4 ] LIU M, SHI P, ZHANG L, et al. Fault-tolerant control for nonlinear Markovian jump systems via proportional and derivative sliding mode observer technique[J]. IEEE Transactions on Circuits and Systems Ⅰ: Regular Papers, 2011,58(11):2755-2764.

[ 5 ] ZHAO J, DIMIROVSKI G M. Quadratic stability of a class of switched nonlinear systems[J]. IEEE Transactions on Automatic Control, 2004,49(4):574-578.

[ 6 ] CHEN B, LIU X, TONG S. Robust fuzzy control of nonlinear systems with input delay[J]. Chaos, Solitons & Fractals, 2008,37(3):894-901.

[ 7 ] LIN C, WANG Q G, LEE T H, et al. Observer-basedH∞fuzzy control design for T-S fuzzy systems with state delays[J]. Automatica, 2008,44(3):868-874.

[ 8 ] ZHANG B, ZHOU S, LI T. A new approach to robust and non-fragileH∞control for uncertain fuzzy systems[J]. Information Sciences, 2007,177(22):5118-5133.

[ 9 ] QI R, BRDYS M A. Stable indirect adaptive control based on discrete-time T-S fuzzy model[J]. Fuzzy Sets and Systems, 2008,159(8):900-925.

[10] 吕欢欢,杨红. 控制器切换下不确定模糊系统的输出反馈[J]. 沈阳大学学报(自然科学版), 2013,25(6):472-475. (LYU H H, YANG H. Output feedback research on uncertain fuzzy systems under controller switching[J]. Journal of Shenyang University(Natural Science), 2013,25(6):472-475.)

[11] WANG W J, CHEN Y J, SUN C H. Relaxed stabilization criteria for discrete-time T-S fuzzy control systems based on a switching fuzzy model and piecewise Lyapunov function[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2007,37(3):551-559.

[12] OHTAKE H, TANAKA K, WANG H O. Switching fuzzy controller design based on switching Lyapunov function for a class of nonlinear systems[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2006,36(1):13-23.

[13] 杨红,陶冠男,牛盾,等. 基于观测器的一类不确定切换模糊系统的鲁棒控制[J]. 沈阳大学学报(自然科学版), 2013,25(3):226-230. (YANG H, TAO G N, NIU D, et al. Robust controller for a class of uncertain switched fuzzy systems based on observer[J]. Journal of Shenyang University(Natural Science), 2013,25(3):226-230.)

[14] 刘扬正, 姜长生, 林长圣, 等. 一类切换混沌系统的实现[J]. 物理学报, 2007,56(6):3107-3112. (LIU Y Z, JIANG C S, LIN C S, et al. A class of switchable 3D chaotic systems[J]. Acta Physica Sinica, 2007,56(6):3107-3112.)

[15] LEE H J, PARK J B, CHEN G. Robust fuzzy control of nonlinear systems with parametric uncertainties[J]. IEEE Transactions on Fuzzy Systems, 2001,9(2):369-379.

【责任编辑: 肖景魁】

Stability Analysis for a Class of Stochastic Switched Fuzzy Systems Based on T-S Model

ZhangLe,GuoChunpeng,GuanChen,LiZhi,YangHong

(School of Information Engineering, Shenyang University, Shenyang 110044, China)

Mean square stabilization of a class of uncertain stochastic switched fuzzy systems based on T-S model is proposed using switching technology. Based on the multiple Lyapunov function methods and linear matrix inequality(LMI), state feedback controllers of stochastic switched fuzzy systems are designed. Sufficient conditions and switching strategy achieving system global asymptotic stability of the system is discussed. In this model, each subsystem of switched system is a stochastic fuzzy system. When some subsystems are unstable, the whole stochastic switched fuzzy system stabilization is obtained by design the appropriate switching law. The design feasibility and effectiveness are illustrated by simulation.

stochastic; switch; fuzzy; mean square stabilization; switching law

2016-11-07

国家自然科学基金资助项目(61004039); 辽宁省自然科学基金指导计划项目(201602529).

张 乐(1975-),男,辽宁沈阳人,沈阳大学副教授,博士后研究人员.

2095-5456(2017)02-0107-06

TP 13

A