Hidden Vacuum Rabi Oscillations:Dynamical Quantum Superpositions of On/OffInteraction between a Single Quantum Dot and a Microcavity

A.Ridolfo,R.Stassi,and O.Di Stefano,∗

1Dipartimento di Scienze Matematiche e Informatiche,Scienze Fisiche e Scienze della Terra,Universit`a di Messina,I-98166 Messina,Italy

2CEMS,RIKEN,Saitama 351-0198,Japan

1 Introduction

Strong coherent interactions between quantum emitters(QEs)and photons play a key role in several schemes for the realization of quantum logic gates[1−3]and quantum networks.[4−5]A quantum phase gate operating on quantum bits carried by a single Rydberg atom and a zero-or one-photon field in a high-Q cavity has been demonstrated.[6]It has been shown that a cavity with a single trapped atom,can be exploited to realize scalable,fully functional photonic quantum computation.[7]The implementation of quantum information processing with cavity quantum electro-dynamical(CQED)systems requires full coherent control of superpositions of cavity coupled and-uncoupled atomic levels.[3,6−7]The superposition principle is at the heart of the most intriguing features of quantum mechanics.

A QE-microcavity system enters the strong coupling regime provided the coherent coupling overwhelms the dissipative processes.In this case a striking change in the system dynamics from the usual irreversible spontaneous emission to a reversible exchange of energy between the emitter and the cavity mode can be observed.[6]As shown in Ref.[8]for a three-level atom,if the emitter is set into a superposition state of one state strongly coupled with the cavity mode and one other state which is uncoupled,it is possible to prepare a quantum system which is“suspended” between two completely different time evolutions.When a measurement is performed,only one of these possible dynamics is actualized.

Here we extend previous work on three-level atoms into a superposition of two different dynamical states.[8]Specifically,(i)we show that it is possible to prepare quantum superpositions of on/offstrong coupling between a microcavity and a single quantum dot(QD);(ii)we demonstrate that these superposition effects can also be observed in nonequilibrium steady state spectra of such dissipative quantum systems under continuous-wave excitations;(iii)we calculate the joint probability of detecting a cavity photon at timet1and a free photon from the decay of the exciton level att2which shows intriguing time-dependent correlation effects and detection-conditioned dynamics.Surprisingly,this two-times correlation function shows that the presence of a subsequent detection event affects the previous photonic dynamics,although causality is not(of course)violated.

Moreover we show that the resulting system dynamics, “suspended”between two different time evolutions,can be directly probed by comparing ordinary and coincidence photodetection.Such dynamics superpositions enable novel counterintuitive nonclassical effects.Situations are possible where cavity photons as well as the emitter luminescence display a weak-coupling exponential decay but their joint detection probability displays a strong-coupling dynamics.Remarkably we find that,these quantum correlations are also present in the nonequilibrium steady state,which is reached under the influence of coherent continuous-wave driving and dissipation.In the last years the strong coupling of semiconductor selfassembled QDs to single modes of monolithic optical cavities was achieved[9−10]opening the possibility of realizing quantum information tasks in solid-state CQED systems.The quantum nature of such strongly coupled excitonphoton system has been proved.[11]Moreover,substantial progress has been made demonstrating the capability of a single QD coupled to a photonic crystal microcavity to control phase modulation of light at single photon level.[12]It has been shown that a non-adiabatic full time control of the strong light-matter interactions of cavity embedded single QE can be realized in principle.[13]Strong coupling in a single QD-semiconductor microcavity system was achieved by coupling the optical mode of a photonic crystal or a micropillar microcavity to the excitonic transition of the QD.In order to realize on/offquantum superpositions we propose,instead,to tune the mode energy of the microcavity to the biexciton-exciton(XX-X)transition of the QD.A similar four-level biexciton-exciton cascade configuration was theoretically investigated in order to analyze the simultaneous formation and stable propagation of slow optical soliton pairs in semiconductor QD.[14]Two electron-hole pairs(a biexciton)trapped in a QD recombine radiatively through a frequency-nondegenerate two-photon cascade.[15]In a first step,the biexciton decays into one of the two possible optically active singleexciton states(see Fig.1(a))by emitting an XX photon,followed by an excitonic decay to the dot ground state(G)by emitting a second X photon with typically somewhat different energy.[16]Recently an ultrabright source of entangled photon pairs has been obtained by coupling an optical cavity in the form of a photonic molecule to a single QD.[17]The lowest energy photonic mode is resonantly coupled to the XX-X(Y)transition and the other to the X(Y)-G which has a transition energy of about 4 meV higher than the XX-X(Y)transition.In this way the Purcell effect is fully effective for both the transitions greatly improving the extraction efficiency of entangled pairs.

2 The Model

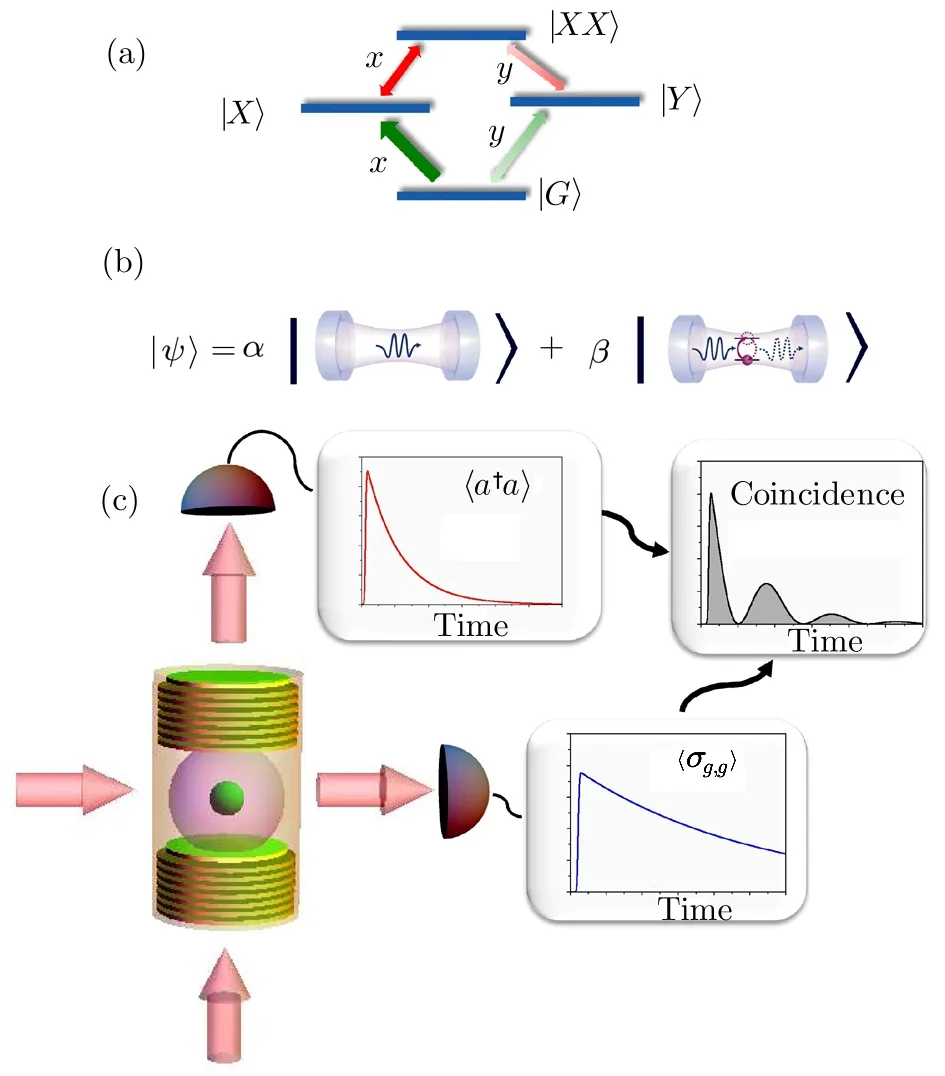
Fig.1 (Color online)(a)Sketch of the radiative cascade in a single QD.See main text for nomenclature.(b)Schematic description of the quantum superposition between a cavity strongly coupled with a two-level atomiclike transition with photons coherently absorbed and reemitted at rate g and a bare cavity(without active material excitation).(c)Sketch of the microcavity embedded QD and of the excitation and detection schemes:quantum superposition(b)enables situations where cavity photons as well as the emitter luminescence display exponential decay but their joint detection probability exhibits vacuum Rabi oscillations.

We consider a single mode microcavity polarized along theˆx(horizontal)direction[18]resonantly coupled with the XX-X transition. The cavity mode polarization greatly suppresses the decay channel XX→Y,being Y-excitons coupled to theˆy polarized photons.The cavity will be also coupled with the transition X-G,although the cavity mode is detuned with respect to this transition by Δ≈4 meV(much larger than the cavity line width).The system is driven by twoˆx-polarized pulsed or continuous wave laser beams(see Fig.1).One beam excites resonantly the cavity mode,the other is resonant with the X-G transition.Other schemes based on circularly polarized beams could also be employed.However the present con figuration works even when the fine-structure splitting cannot be neglected.Before describing the detailed model and supporting calculations, first we summarize the basic ideas of our scheme.We consider onlyh-polarized pulses so that the state|Y〉is not excited.At initial time the cavity is empty(zero photons)and the QE is described by the state|G〉.We point out that the full width at half maximum(FWHM)of the pulse feeding the cavity is chosen less than the Rabi period(FWHM≪π/g).As consequence,the cavity is populated with photons before the energy transfer to the QE starts.The latter process,at the end,allows the coherent excitation cavity.Then anh-polarized control pulse of frequencyωx(ωgis set to zero)resonant with the|G〉→ |X〉transition determines a rotation of the Bloch sphere{|G〉,|X〉}.After creation of the GX superposition,the cavity is excited by a weak resonant coherent pulse.Just after the pulse arrival,the state becomes|ψ′(t)〉=|α〉(aG|G〉+aX|X〉),being|α〉≈ |0〉+α|1〉a coherent photon state.In fact,when the cavity is first excited by a weak probe beam the levels coupled with the cavity are unpopulated,hence cavity photons are not able to couple to the XXX transitions. As a result,cavity photons start decaying exponentially according to the cavity decay time.As soon as the first control pulse excites the cavity the system switches to the strong-coupling regime,as witnessed by the presence of vacuum Rabi oscillations.[19]From now on the two states composing the linear superpositions obey completely different dynamics:|α〉|G〉is a stationary state(except for the cavity losses),while the ket|α〉|X〉evolves under the influence of the strong light matter interaction,which induces photon absorption and re-emission processes before dissipation becomes effective.The evolution of the total quantum state can be schematically visualized as|ψ(t)〉=aX|On(t)〉+aG|Off(t)〉(see Fig.1(b)).We have defined|Off(t)〉=|α〉|G〉that,as observed above,is a stationary state.In addition,we have|On(t)〉t=0=|α〉|X〉.Such state evolves as:|On(t)〉=■aX=0 we have|〈a†a〉=|α|2and as expected the system is in a stationary state;ifaG=0|〈a†a〉=|α|2cos2(gt)giving rise to Rabi oscillations. For the general case(aX/=0 andaG/=0)we obtain a mixed behaviour and the system is suspended between two different dynamics.Once the coupled quantum system is in this superposition state,probing it(e.g.feeding the cavity with a weak probe pulse),will give rise to an output signal with hybrid strong-weak coupling properties which can be probed experimentally.Moreover photons spontaneously emitted into free space from the decay of the exciton level,can be detected and collected in addition to output cavity photons.At last,through a coincidence measurement,it is possible to post-select only cavity photons in the strong coupling regime.

In the absence of losses the optically pumped quantum system depicted in Fig.1 is described by the Hamiltonian

where the Bosonic operatorsa(a†)destroy(create)a cavity photon,andσj,j′ represents the transition operator from the|j′〉to|j〉state.In the above equation the first term in the square bracket describes the interaction of the transition X-XX with cavity photons,being 2gsingle-photon Rabi frequency,Ec(t)is the control optical field driving resonantly the transition G-X,while Ein(t)describes the input field feeding the microcavity.In all subsequent calculations we will use for the single-photon Rabi frequency 2g=200µeV[11]and an XX binding energy Δ =ωxx− 2ωx=4 meV.Losses can be taken into account within the quantum Master equation in Born–Markov approximation for the system density matrixρ,which is expressed in the usual Lindblad form.[20]The relevant Master equation for this model is

where the Lindblad operatorsLµdescribe the various de-zero temperature reservoirs.In all subsequent calculations we will use typical decay rates for state of art QD-microcavity systems.[11]The decay rate for cavity photons isγc=70µeV,the decay rate of the transitionXX→XisγXX→X=30µeV,and that associated to theX→Gtransition isγx→g=20µeV.The influence of pure dephasing noise[21]on the quantum effects under investigation can be addressed including a further term on the righthand side of Eq.(2):

Starting from the above master equation,we may derive the coupled equations of motion for the cavity-photon and exciton populations,coherences and higher order correlation functions,which we solve by representing the photon operators on a basis of Fock number states.

According to the input-output formulation of optical cavities,the external field is related to the intracavity field by the relation[22−23]

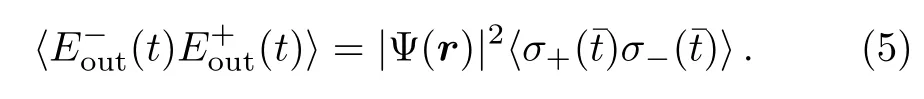
In the present case,considering the light field emitted by the exciton levelX,we haveσ−=σgx.

3 Numerical Results

Let us consider the time resolved response after the arrival of fast optical pulses. At initial time,a weak Gaussian control pulse(resonant with the transition GX;pulse area=0.012π)performs a very small rotation of the Bloch sphere{|G〉,|X〉}giving rise to a superposition|ψ(t)〉=|0〉(ag|G〉+ax|X〉)with|ax|2≪ |ag|2.Immediately after(3 ps delay)a weak probe beam(pulse area=0.02π)resonant with the bare cavity-mode feeds the microcavity.The time-duration(FWHM)of both pulses is 5 ps.In Fig.2,we present our numerical results for experimentally accessible observables of the system.In Fig.2(a)we plot the time dependence of the cavity average photon number 〈a†a〉,which is proportional to the detectable output transmitted photon fluxif the input field at the output port is in the vacuum state.It displays irreversible exponential decay mainly due to photon escape through the cavity mirrors,which is a signature of weak(or even absence of)light-matter interaction.Observation of the vacuum Rabi splitting or,in the time domain,vacuum Rabi oscillations,requires that the effective coupling rate(known to scale with the electronic population difference among the involved levels)exceeds the mean of the decay rates of the cavity and of the electronic transition.In a semiclassical picture,the effective coupling rate is given byIn the present case,owing to the smallness of〈σx,x〉as well as of〈σxx,xx〉,the system displays a weak coupling regime behavior.The superimposed small and fast oscillations originate from the coupling of the cavity with the detuned X-G transition.Figure 2 also shows the level|X〉population dynamics which also exhibits irreversible Markovian behavior,due to spontaneous emission.

Fig.2 (Color online)Time evolution of cavity photons〈a†a〉,of spontaneously emitted photons from the exciton level ∝ 〈σx,x〉,and the coincidence rate of detecting one cavity photon and one photon from the spontaneous transition|X〉→ |G〉which is proportional to Ixc= 〈a†aσx,x〉( filled curve)after the arrival of two weak optical pulses exciting resonantly both the cavity and the|G〉→|X〉transition;while the first two expectation values display almost exponential irreversible decay,the third exhibits vacuum Rabi oscillations.It also displays Ixccalculated including pure dephasing.For the adopted parameters see text.

Spontaneously emitted photons at frequencyωxradiated out the side of the cavity,are proportional to 〈σx,x〉.Hence it is possible to gather direct information on both the cavity-photon population(by detecting photons escaping from one cavity mirror atωc=ωxx−ωxand on〈σx,x〉.In Fig.2(a)we also plot the time behavior of the joint probability of detecting one cavity photon and one photon from the spontaneous transition|X〉→|G〉which is proportional toIxc= 〈a†aσx,x〉.This coincidence rate,a subset of the Markovian signals 〈σx,x〉and 〈a†a〉,displays almost perfect vacuum Rabi oscillations.

It is worth noticing that the detected joint signal will actually be proportional to the joint output field intensitieswhich in turn is proportional toIxc=Hence the actually measured joint dynamics is correctly described byIxc.We also observe that the cavity is efficient and emits the photons directionally(in the cavity axis),while the emitter is long-lived,emits weakly,and isotropically.As a consequence the experimental observation of such a joint detection rate will require much longer acquisition times than those required for the acquisition of.Figure 2(a)also displaysIxccalculated including additional pure dephasing.We adopted=15µeV and=20µeV.The observed effect reveals robust against a significant amount of pure dephasing which just reduces the amplitude of vacuum Rabi oscillations.This is an interesting example of correlated quantum dynamics induced by the quantum superpositions of on/offstrong coupling between a microcavity and a single QD.The optical observables here addressed,display nonclassical behavior,as can be inferred from the violation of the Cauchy–Schwarz inequality for classical correlations:[20]

whereis the zero-delay twomode normalized second-order intensity correlation function and(t,t)are the corresponding single-mode normalized second-order correlation functions for cavity photons and photons emitted from the spontaneous decay of levelX,respectively.

In order to explore more deeply such quantum correlated dynamics,we calculate the joint probability of detecting a cavity photon att1and one photon from the decay of levelXatt2(see Fig.3(a)):

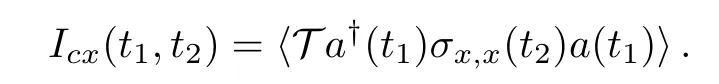
The symbol T denotes time ordering:e.g.ift1＞t2,

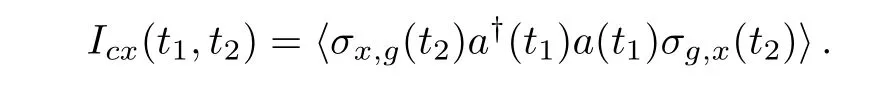
The figure shows a clear coexistence of exponential decay an Rabi oscillations.Such coexistence is a signature of the “suspended” dynamics between two completely different time evolutions induced by the quantum superposition|ψ(t)〉=a|On(t)〉+b|Off(t)〉.Such behavior can be better understood looking at line cuts obtained fixingt1=ort2=.For example the functions C¯t2(t)=Icx(t,)display an oscillatory behavior fort＜and an exponential decay fort＞.An analogous behavior is exhibited by X¯t1(t)=Icx(,t).Hence the presence of a subsequent detection event affects the previous photonic dynamics.On the other hand a detection event e.g.at timedetermines a collapse of the wavefunction affecting the dynamics for the following timest＞¯t2.Figure 3(b)shows the normalized joint probability of detecting a cavity photon att1and one photon from the decay of levelXatt2:

〈a†aσx,x〉under continuous-wave excitation as a function of the frequency of the input field feeding the microcavity Ein=0.003.In this calculation we will use for the singlephoton Rabi frequency 2g=100µeV and an XX binding energy Δ =ωxx−2ωx=4 meV.The system is also excited with a weak monochromatic field control pulse Ec=0.001 driving resonantly the transition G-X.While 〈a†a〉displays a single peak at the cavity-mode energy,characteristic of a system in the weak-coupling regime,Ixcexhibits the vacuum Rabi splitting.Results in Fig.3(c)demonstrate that the conditional quantum dynamics induced by the quantum superposition|ψ(t)〉=a|On(t)〉+b|Off(t)〉is also present in the nonequilibrium steady state of this coherently driven dissipative quantum systems.

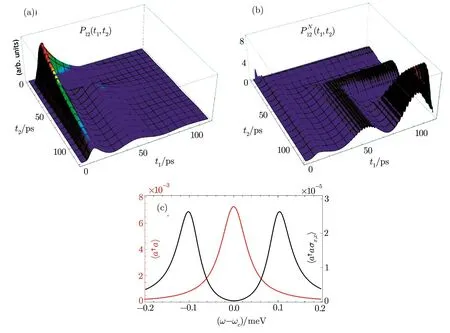
Fig.3 (Color online)(a)Joint probability of detecting a cavity photon at t1and one photon from the decay of level X at t2:P1,2(t1,t2)=Icx(t1,t2).(b)Normalized joint probability of detecting a cavity photon at t1and one photon from the decay of level X at t2:PN 1,2(t1,t2)=Icx(t1,t2)/〈a†a〉〈σ†gxσgx〉after two pulse excitation as in Fig.2.(c)Cavity photon number 〈a†a〉and coincidence rate Ixc= 〈a†aσx,x〉under continuous-wave excitation as a function of the frequency of the input field feeding the microcavity Ein.The system is also excited with a weak monochromatic field Ec driving resonantly the transition G-X.

4 Conclusions

We have theoretically investigated the time-and frequency-resolved spectroscopic signatures of quantum superpositions of on/offstrong coupling between a microcavity and a single QD The resulting system dynamics, “suspended” between two different time evolutions,has been discussed using readily accessible optical observables.The experimental preparation and observation of the proposed dynamics in a single QD-semiconductor microcavity system is within experimental reach with existing state-of-the-art technology.[16,24]Possible experimental issues can originate from the excitonic emission,which is not directional and can be weak with respect to the cavity emission.However,since only coincidence events are recorded in such(coincidence)experiments,attenuation of the stronger signal or low efficient collection of the other signal does not alter the normalized cross-correlation functions.It determines only an increase of the events not displaying coincidences,which will be discarded(post selection),resulting just into an increase of the acquisition times.An interesting example of cross correlation measurements in a cavity embedded single QD has been reported in Ref.[11].The effects here described can also be studied in novel ultracompact hybrid structures composed by a single QD strongly coupled via localized surface plasmons to one or a couple of metallic nanoparticles.[25−26]Laser cooling of the center-of-mass motion of such hybrid system has been recently proposed.[27]Realization of On-Offinteraction superpositions in these mesoscopic systems can result into quantum superpositions of motional states.The scheme here proposed,based on tuning the mode energy of the microcavity to the biexciton-exciton(XX-X)transition of the QD,could be exploited for the solid state implementation of scalable quantum computation with single-photon polarizations as qubits.[7]It would also be interesting to extend such quantum control in optically active many-body quantum systems.[28−32]and in quantum optical systems in the ultrastrong coupling regime.[33−36]

References

[1]T.Pellizzari,S.A.Gardiner,J.I.Cirac,and P.Zoller,Phys.Rev.Lett.75(1995)3788.

[2]M.S.Zubairy,M.Kim,and M.O.Scully,Phys.Rev.A 68(2003)033820.

[3]C.Monroe,Nature(London)416(2002)238,for a review,see.

[4]J.I.Cirac,P.Zoller,H.J.Kimble,and H.Mabuchi,Phys.Rev.Lett.78(1997)3221.

[5]S.Ritter,C.Nöleke,C.Hahn,et al.,Nature(London)484(2012)195.

[6]J.M.Raimond,M.Brune,and S.Haroche,Rev.Mod.Phys.73(2001)565.

[7]L.M.Duan and H.J.Kimble,Phys.Rev.Lett.92(2004)127902.

[8]R.Stassi,A.Ridolfo,S.Savasta,R.Girlanda,and O.Di Stefano,Europhys.Lett.99(2012)24003.

[9]J.P.Reithmaier,G.Sek,A.Loffer,C.Hofmann,S.Kuhn,S.Reitzenstein,L.V.Keldysh,V.D.Kulakovskii,T.L.Reinecke,and A.Forchel,Nature(London)432(2004)197.

[10]T.Yoshie,A.Scherer,J.Hendrickson,et al.,Nature(London)432(2004)200.

[11]K.Hennessy,A.Badolato,M.Winger,et al.,Nature(London)445(2007)896.

[12]I.Fushman,D.Englund,A.Faraon,et al.,Science 320(2008)769.

[13]A.Ridolfo,R.Vilardi,O.Di Stefano,S.Portolan,and S.Savasta,Phys.Rev.Lett.106(2011)013601.

[14]W.X.Yang,A.X.Chen,R.K.Lee,and Y.Wu,Phys.Rev.A 84(2011)013835.

[15]R.J.Young,R.M.Stevenson,P.Atkinson,et al.,New J.Phys.8(2006)29.

[16]E.Moreau,I.Robert,L.Manin,et al.,Phys.Rev.Lett.87(2001)183601.

[17]A.Dousse,et al.,Nature(London)466(2010)217.

[18]M.Winger,A.Badolato,K.J.Hennessy,et al.,Phys.Rev.Lett.101(2008)226808.

[19]O.Di Stefano,A.Ridolfo,S.Portolan,and S.Savasta,Opt.Lett.36(2011)4509.

[20]L.Mandel and E.Wolf,Optical Coherence and Quantum Optics,Cambridge University Press,Cambridge(1999).

[21]A.Auff´eves,D.Gerace,J.M.G´erard,et al.,Phys.Rev.B 81(2010)245419.

[22]D.F.Walls and G.Milburn,Quantum Optics,Springer-Verlag,Berlin(1995).

[23]C.W.Gardine and P.Zoller,Quantum Noise,2nd ed.,Springer-Verlag,Berlin(2000).

[24]J.Bochmann,M.Mucke,G.Langfahl-Klabes,et al.,Phys.Rev.Lett.101(2008)223601.

[25]A.Ridolfo,O.Di Stefano,N.Fina,et al.,Phys.Rev.Lett.105(2010)263601.

[26]S.Savasta,R.Saija,A.Ridolfo,et al.,ACS Nano 4(2010)6369.

[27]A.Ridolfo,R.Saija,S.Savasta,et al.,ACS Nano 5(2011)7354.

[28]G.Slavcheva and P.Roussignol,(Eds.),Optical Generation and Control of Quantum Coherence in Semiconductor Nanostructure,1st ed.,Springer(2010).

[29]S.Portolan,O.Di Stefano,S.Savasta,and V.Savona,Europhys.Lett.88(2009)20003.

[30]O.Di Stefano,S.Savasta,and R.Girlanda,J.Mod.Opt.48(2001)67.

[31]S.Portolan,O.Di Stefano,S.Savasta,et al.,Phys.Rev.B 77(2008)035433.

[32]S.Portolan,O.Di Stefano,S.Savasta,et al.,Phys.Rev.B 77(2008)195305.

[33]R.Stassi,A.Ridolfo,O.Di Stefano,et al.,Phys.Rev.Lett.110(2013)243601.

[34]L.Garziano,R.Stassi,V.Macr`ı,et al.,Phys.Rev.A 92(2015)063830.

[35]L.Garziano,V.Macr`ı,R.Stassi,et al.,Phys.Rev.Lett.117(2016)043601.

[36]O.DiStefano, R.Stassi, L.Garziano,etal.,New J.Phys.(2017); https://doi.org/10.1088/1367-2630/aa6cd7;arXiv:1603.04984.