Super W1+∞ n-Algebra in the Supersymmetric Landau Problem∗

Chun-Hong Zhang(张春红),Lu Ding(丁璐),Zhao-Wen Yan(颜昭雯),Ke Wu(吴可),and Wei-Zhong Zhao(赵伟忠),†

1School of Mathematical Sciences,Capital Normal University,Beijing 100048,China

2Institute of Applied Mathematics,Academy of Mathematics and Systems Science,Chinese Academy of Sciences,Beijing 100190,China

3School of Mathematical Sciences,Inner Mongolia University,Hohhot 010021,China

1 Introduction

Since Nambu[1]proposed 3-bracket for the generalized Hamiltonian dynamics,the higher order algebraic structures and their possible physical applications have attracted much interest.Recently the in finite-dimensionaln-algebras have received considerable attention.[2−7]As an important in finite-dimensional algebra,theW∞algebra has been studied intensely from a variety of viewpoints.Based on the structure ofW∞algebra,Chakrabortty et al.[3]investigated theW∞3-algebra.By applying a double scaling limits on the generators,they obtained aw∞3-algebra,which satis fies the so-called fundamental identity(FI).Chen et al.[5]presented the superw∞3-algebra and gave its realization in terms of the super Nambu–Poisson bracket.Quite recently theW1+∞3-algebra has also been studied.The relation between this in finite-dimensional 3-algebra and the integrable systems has been established in the framework of Nambu mechanics.[8]

It is well-known that theW1+∞algebra has the important applications in the free electron theory of Landau levels and the quantum Hall effect.[9−13]It was found that the supersymmetric extension of theW1+∞algebra also appears in the supersymmetric Landau problem.[14]Recently the applications of then-algebra in condensed matter physics have attracted a lot of interests.TheA-class topological insulators can be regarded as a higher dimensional counterpart of the quantum Hall effect.Hasebe[15]constructed the chiral topological insulator(AIII-class)with Landau levels based on the Nambu 3-algebraic geometry.Estienne et al.[16]investigated then-algebraic structure of topological insulators.More recently we have reinvestigated the Landau problem and presented theW1+∞n-algebraic structure in this physical system.[17]In this paper,we shall investigate the supern-algebra and present the superW∞n-algebra in the supersymmetric Landau problem.

2 Supern-algebra

LetBibe arbitrary associative operators.The super multibracket of ordernis defined by[18]

where|Bi|is the parity ofBi.For the bosonic operators,Eq.(1)becomes then-commutator

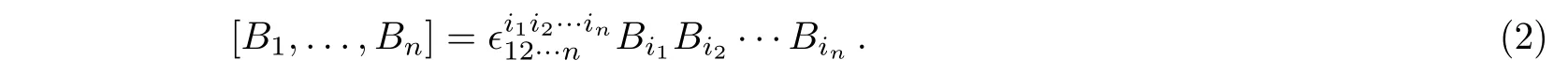
The first few super multibrackets are as follows:

(i)n=2

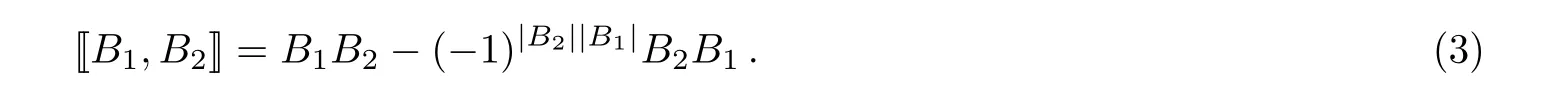
It is the well-known Lie super bracket.

(ii)n=3

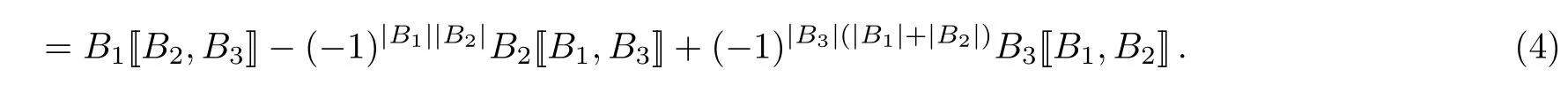
(iii)n=4

According to the definition(1),we have the skewsymmetry

Whennis even,the super multibracket(1)satisfies the generalized super Jacobi identity(GSJI)[18]

For the generatorsXi,the generalized super Lie algebra of ordern=2kis defined by an expression of the form that satisfies the GSJI(7)

where the multibracket is defined by Eq.(1)andCji1i2···i2kare the structure constants.

For the oddn-brackets(2)built from associative operator products,it is known that they satisfy the generalized Bremner identity(GBI)[19−22]

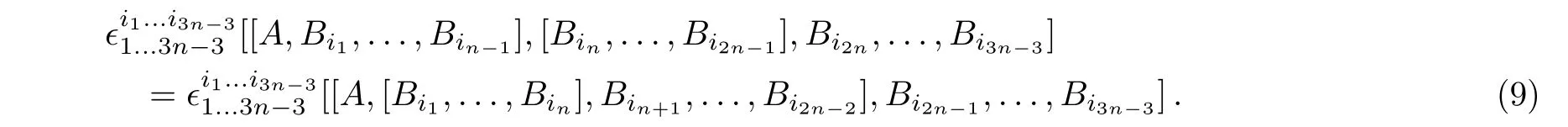
However for the case of the super oddn-brackets,the corresponding generalized super Bremner identity(GSBI),to our best knowledge,has not been reported so far in the existing literature.Let us deal with it below.

Based on the definition ofnbracket(1),we have

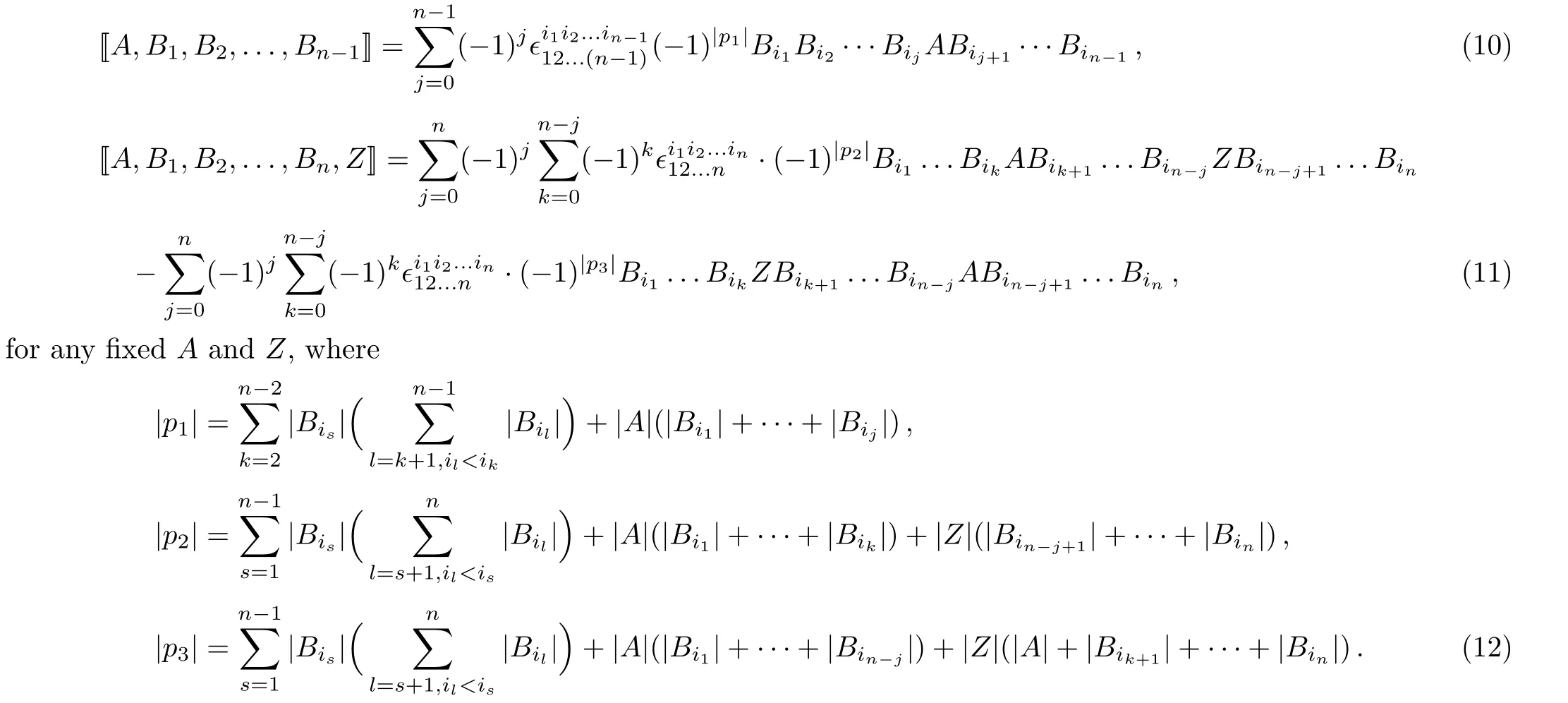
By means of Eqs.(10)and(11),we can show(see Appendix)that whennis odd,the supern-bracket(1)satisfies the following GSBI:For the case of the bosonic operators,Eq.(13)gives the GBI(9).

3 SuperW1+∞n-algebra in the Supersymmetric Landau Problem

Let us consider a supersymmetric Landau problem,where the Hamiltonian is given by[14]

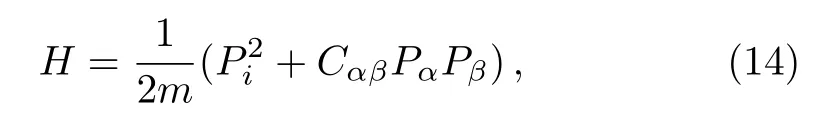
in whichCαβdenotes theα-th row andβ-th column element in a charge conjugation matrix

the covariant momenta are given byPi= −i(■∂i+ϵ11=ϵ22=0,ϵ12= −ϵ21=1,∂i=(∂/∂xi)(i=1,2)and∂α=(∂/∂θα)(α=1,2),B˜ is a constant magnetic strength,xiandθαare the bosonic and fermionic coordinates,respectively.

Let us introduce dimensionless complex coordinates and derivatives as follows:

where≡1/is the magnetic length.

In the symmetric gauge,we may define the bosonic creation and annihilation operators

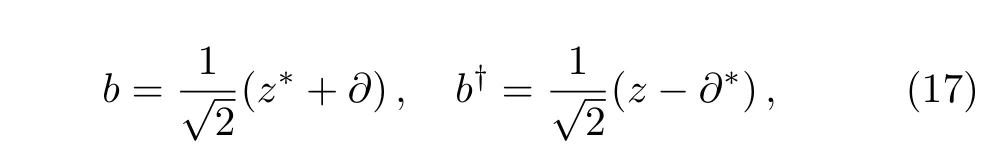
and the fermionic creation and annihilation operators

They satisfy[a,a†]=[b,b†]=1 and{α,α†}={β,β†}=1.Other(anti)commutators are zeros.

In terms of the creation and annihilation operators,the Hamiltonian(14)can be rewritten as[14]

We may also express the angular momentumL⊥as

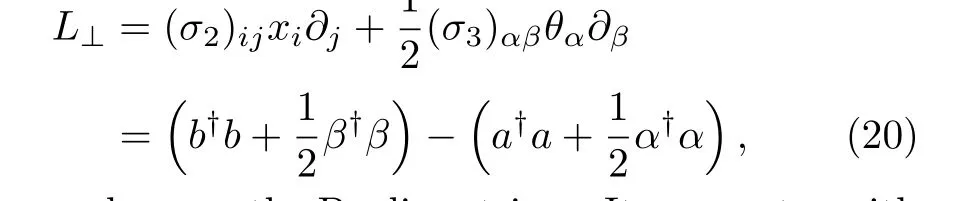
whereσ2andσ3are the Pauli matrices.It commutes with the Hamiltonian(19).

Let us take the operators

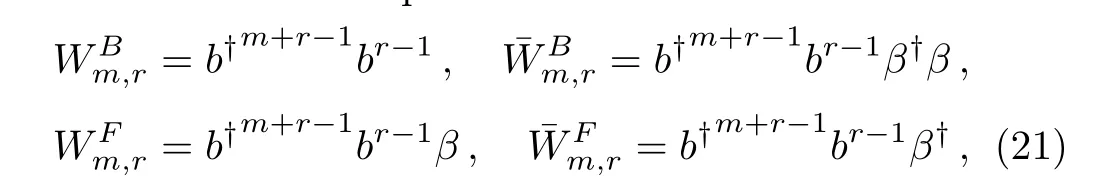
wherer≥1 andm+r≥1,the superindicesBandFdenote the corresponding operators being the bosonic and fermionic ones,respectively.It can be very easily seen that the operators(21)commute with the Hamiltonian(19).It indicates that they are indeed the in finite conserved operators.

By calculating the(anti)commutation relations,we find that the in finite conserved operators(21)yield the superW1+∞algebra¯

m=m1+m2and¯r=r1+r2−1−α1.In the bosonic limit,Eq.(22)reduces to theW1+∞algebra.[9]

For the in finite conserved operators(21),the commutation relations with the angular momentum are given by

Let us turn to the super 3-bracket(4).By means of Eq.(23),we may derive the following super 3-brackets:

From Eq.(24),we note that these super 3-brackets are not closed.However for the particular bosonic operators

It should be pointed out that for the fermionic ones,there do not exist such kinds of null 3-brackets.

Substituting the operators(21)into the super 3-bracket(4),we may derive the superW1+∞3-algebra.Due to too many 3-algebra relations,let us focus on the operatorsWBm,randWFm,r.They yield the sub-3-algebra

According to the result in the previous section,the GSBI(13)may be con firmed to hold for the superW1+∞sub-3-algebra(26).However it is not difficult to show that Eq.(26)does not satisfy the GSJI(7)and super FI[23]

other(anti)commutators are zeros.Moreover these operators also yield the super Virasoro–Witt 3-algebra

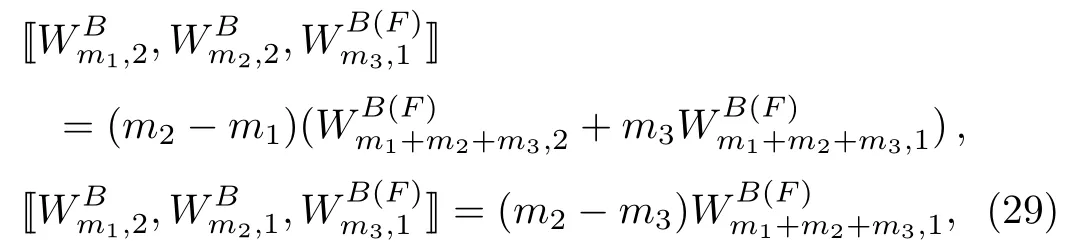
other 3-(anti)commutators are zeros.As a sub-3-algebra of Eq.(26),the forms of super Virasoro–Witt 3-algebra(29)are simple.Although the GSBI(13)is guaranteed to hold for Eq.(29),we find that the GSJI(7)and super FI(27)still fail for it.

Let us turn to the case ofn-algebra.Substituting the in finite conserved operators(21)into the supern-bracket(1)we can in principle derive the superW1+∞n-algebra.However the form of the higher order structure constants appears to become more complicated due to the mixed product of the bosonic and fermionic generators,it is hard to give the all explicit expressions of multibrackets.For this reason,here we only focus on the generatorsand.Performing straightforward calculations,we obtain the supern-algebra

Due to the associative operators,the superW1+∞nalgebra(30)withneven is the so-called generalized Lie algebra which satis fies the GSJI(7).Whennis odd,the GSBI(13)is guaranteed to hold for it.

It is known that there exists the nontrivial sub-2nalgebra in theW1+∞2n-algebra.[17]Let us turn to the supersymmetric case.For the generatorsandwith any fixed subindexn+1≥2,we find that they yield the super sub-2n-algebra

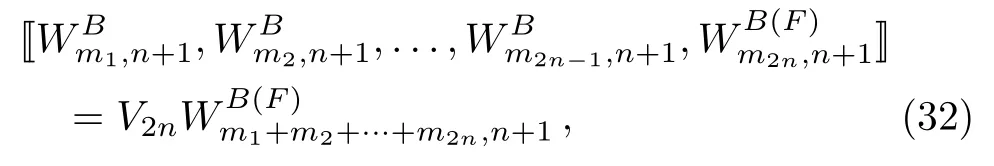
other 2n-(anti)commutators are zeros,where we take the scaled generators

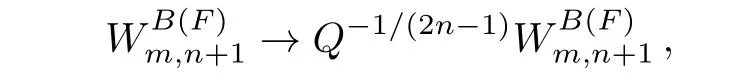
the scaling coefficientQis given by

S2n−1is the permutation group of{1,2,...,2n−1},V2nis the so-called Vandermonde determinant

Note that the superW1+∞sub-2n-algebra(32)satis fies the GSJI(7),however it can be shown that Eq.(32)does not satisfy the super FI[23]

Thus Eq.(32)is a generalized super Lie algebra not a super Filippov algebra.As the examples,let us list the first two superW1+∞sub-2n-algebras.

(i)For the generatorsand,we have the super sub-4-algebra

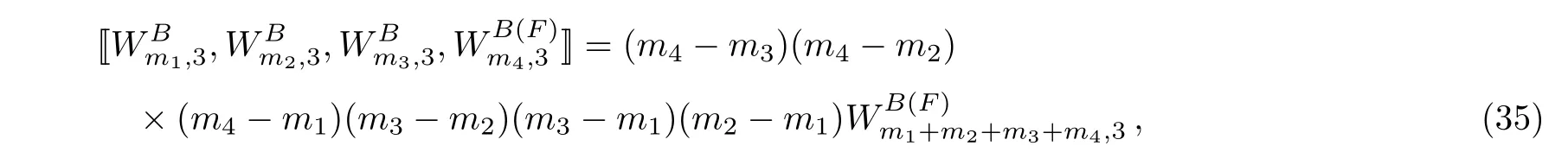
other 4-(anti)commutators are zeros.

(ii)For the generatorsandwe have the super sub-6-algebra

other 6-(anti)commutators are zeros.

4 Summary

We analyzed the supern-bracket built from associative operator products.Whennis even,one has known that the corresponding super multibracket satisfies the GSJI.We investigated thenodd case and gave the corresponding GSBI.It is well-known that there exist the in finite conserved operators,which form the superW1+∞algebra in the the supersymmetric Landau problem.We reinvestigated these in finite conserved operators and found that besides the superW1+∞algebra,they also yield the superW1+∞n-algebra,which satisfies the GSJI and GSBI for theneven and odd cases,respectively.Moreover we gave the superW1+∞sub-2n-algebra.It should be stressed that its structure constants are determined by the so-called Vandermonde determinant.Our analysis suggested that there are the remarkable properties for the superW1+∞n-algebra,more applications of this in finite-dimensionaln-algebra in physics should be of interest.

Appendix A Proof of Eq.(13)

For convenience,we denote

where{σ1,...,σn}and{τ1,...,τn}are the permutations of{1,...,n}.

Let us taken=2r+1.By means of the relation of L´evi–Civit`a symbol

the left side of Eq.(13)becomes

Taking A=[[A,Bi2r,...,Bi4r−1]],Z=Bi4rBi4r+1···Bi6rand using Eq.(11),we can rewrite Eq.(A3)as

By means of Eq.(10),we have

Substituting Eq.(A5)into Eq.(A4),we obtain

where

Proceeding likewise,we may derive the right side of Eq.(13)to be equal to Eq.(A6).Now we complete the proof.

References

[1]Y.Nambu,Phys.Rev.D 7(1973)2405.

[2]T.L.Curtright,D.B.Fairlie,and C.K.Zachos,Phys.Lett.B 666(2008)386.

[3]S.Chakrabortty,A.Kumar,and S.Jain,J.High Energy Phys.09(2008)091.

[4]M.Axenides and E.Floratos,J.High Energy Phys.02(2009)039.

[5]M.R.Chen,K.Wu,and W.Z.Zhao,J.High Energy Phys.09(2011)090.

[6]L.Ding,X.Y.Jia,K.Wu,Z.W.Yan,and W.Z.Zhao,Nucl.Phys.B 904(2016)18.

[7]S.K.Yao,L.Ding,P.Liu,C.H.Zhang,and W.Z.Zhao,Commun.Theor.Phys.66(2016)423.

[8]M.R.Chen,S.K.Wang,X.L.Wang,K.Wu,and W.Z.Zhao,Nucl.Phys.B 891(2015)655.

[9]A.Cappelli,C.A.Trugenberger,and G.R.Zemba,Nucl.Phys.B 396(1993)465.

[10]I.I.Kogan,Int.J.Mod.Phys.A 9(1994)3887.

[11]A.Capelli,C.Trugenberger,and G.Zemba,Phys.Rev.Lett.72(1994)1902.

[12]S.Iso,D.Karabali,and B.Sakita,Phys.Lett.B 296(1992)143.

[13]H.Azuma,Prog.Theor.Phys.92(1994)293.

[14]K.Hasebe,Phys.Rev.D 72(2005)105017.

[15]K.Hasebe,Nucl.Phys.B 886(2014)681.

[16]B.Estienne,N.Regnault,and B.A.Bernevig,Phys.Rev.B 86(2012)241104(R).

[17]C.H.Zhang,L.Ding,Z.W.Yan,K.Wu,and W.Z.Zhao,arXiv:hep-th/1606.07570v2.

[18]P.Hanlon and M.Wachs,Adv.Math.113(1995)206.

[19]M.R.Bremner,J.Algebra 206(1998)615.

[20]M.R.Bremner and L.A.Peresi,Linear Algebra Appl.414(2006)1.

[21]T.Curtright,X.Jin,and L.Mezincescu,J.Phys.A:Math.Theor.42(2009)462001.

[22]C.Devchand,D.Fairlie,J.Nuyts,and G.Weingart,J.Phys.A:Math.Theor.42(2009)475209.

[23]N.Cantarini and V.G.Kac,Commun.Math.Phys.298(2010)833.