巴西圆盘劈裂破坏的近场动力学建模与分析

韩志腾+秦洪远+刘一鸣+黄丹

摘要： 基于非局部近场动力学（Peridynamics，PD）理论，对含预置裂纹的混凝土巴西圆盘劈裂破坏问题进行建模分析.将结构离散为包含混凝土材料信息的粒子，引入动态松弛、分级加载和失衡力守恒等粒子系统数值算法，构建可以自然模拟脆性裂纹扩展的PD算法体系.对含不同角度单预置中心裂纹巴西圆盘的裂纹扩展过程进行数值模拟，所得结果与试验结果吻合较好，验证所提出的模型和算法正确.进一步采用该方法模拟双预置裂纹巴西圆盘劈裂破坏过程中的裂纹扩展、交汇、贯通过程，通过将所得模拟结果与试验结果进行比较分析，探究该方法处理多裂纹扩展问题的可行性.

关键词： 巴西圆盘； 劈裂破坏； 近场动力学； 非局部理论； 微极模型； 多裂纹； 脆性材料

中图分类号： TU37文献标志码： A

Abstract： The concrete cracked chevron notched Brazilian disks with split are modeled and analyzed based on the nonlocal Peridynamic（PD） theory. The structure is discretized as material points containing concrete material information， and a series of numerical algorithms of particle system including dynamic relaxation， stepbystep loading and nonequilibrium criterion are introduced into the framework of PD for naturally simulating crack growth. The crack propagation process of Brazilian disks with single preexisting central crack under different initial angles is numerically simulated， and the result is in good consistence with the test result， which verifies the proposed model and algorithm. The crack propagation， intersection and coalescence process in doublenotched Brazilian disks are simulated by the method. The feasibility to study multiple crack growth problems using the proposed method is investigated through the comparison and analysis of the simulation results and the test results.

Key words： Brazilian disk； split failure； peridynamics； nonlocal theory； micropolar model； multiple cracks； brittle material

0引言

混凝土是典型的準脆性拉压异性材料和主要的工程材料，其裂纹的出现和扩展往往由局部或整体承受拉应力所引起.目前主要存在2类试验方法分析材料的拉伸特性：其一为直接拉伸试验，由于混凝土材料自身的非均匀性，直接拉伸试验往往存在偏心力，常导致试验结果不能正确反映材料的拉伸特性；其二为间接拉伸试验，该方法可避免直接拉伸试验中存在的限制，能够更为准确地分析混凝土类材料的拉伸特性，其中以巴西圆盘劈裂拉伸试验[1]最受关注.

为对巴西圆盘的静态和动态破坏进行分析，国内外学者进行大量的试验研究和数值模拟，如：HAERI等[2]分别研究含单、双预置裂纹的巴西圆盘试样受对径压缩载荷作用下的裂纹扩展过程，得到不同角度预置裂纹作用下巴西圆盘试件的裂纹扩展路径；钱莹等[3]采用二阶流形元法对冲击载荷作用下巴西圆盘的劈裂拉伸破坏进行数值模拟，所得模拟结果与试验结果吻合较好.陈枫等[4]运用权函数方法对中心裂纹巴西圆盘试样的对径加载复合断裂进行分析，得到较为准确的应力强度因子公式.

基于新兴的非局部近场动力学（Peridynamics， PD）理论[56]分析材料和结构的破坏问题已成为当前计算力学和相关领域的热点.十余年来，国内外研究人员将PD方法应用于混凝土类脆性材料的破坏分析中，如：刘一鸣等[7]基于态型PD理论对混凝土板的裂纹扩展过程进行数值模拟，分析预置裂纹角度对于裂纹扩展路径的影响；郁杨天等[8]采用改进的PMB模型计算冲击载荷作用下单边缺口混凝土梁的破坏全过程；GERSTLE等[9]，HA等[10]和KILIC等[11]分别运用PD方法对脆性材料混凝土构件的冲击破坏、失稳等问题进行分析；笔者所在课题组早期也曾模拟混凝土板的拉压和冲击破坏过程等[1214].

在已有研究基础上，本文基于PD理论，通过引入动态松弛、分级加载、失衡力守恒等粒子系统数值算法，构建能够自然模拟结构由弹性变形到脆性断裂的PD算法体系，并对含不同角度单预置裂纹巴西圆盘受对径压缩载荷作用下的破坏过程进行数值模拟，所得裂纹扩展路径与试验结果吻合较好，验证提出的模型和算法正确.在此基础上，进一步采用本文方法模拟双预置裂纹巴西圆盘受对径压缩载荷作用的裂纹扩展、交汇、贯通过程，并将模拟结果与试验结果进行比较分析，验证所提出的模型和算法在分析多裂纹扩展问题时的可引性.

1PD基本框架

1.1PD基本思想和模型

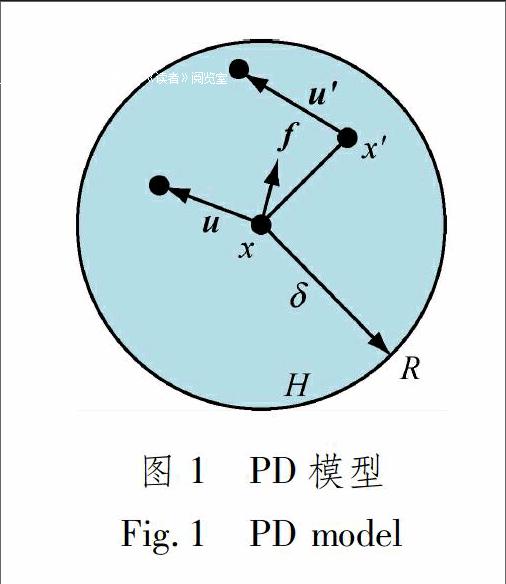
设物体占据空间域R，见图1.对某一时刻t，域内任一物质点x与其邻近一定范围δ（称为近场范围尺寸）内其他物质点存在相互作用力f（点对力），则根据牛顿第二定律可得到关于物质点空间积分形式的运动方程为

2.2含中心单裂纹巴西圆盘劈裂破坏

单预置裂纹巴西圆盘几何参数和加载条件见图4.分析对径压缩载荷作用下的单初始裂纹巴西圆盘，其材料参数和模型尺寸与文献[2]一致，具体为：弹性模量E=15 GPa，泊松比ν=0.21，密度ρ=2 400 kg/m3，抗拉强度ft=3.81 MPa，抗压强度fc=20 MPa，圆盘直径为0.1 m，预置中心裂纹长度2b=0.03 m.物质点间距Δx=0.000 5 m，近场范围δ=3Δx=0.001 5 m，迭代时间步长Δt=0.1 μs.按照文献[2]的试验方案，预置裂纹角度β分别取为0°，15°，30°，45°，60°和90°.

不同角度预置裂纹的圆盘裂纹扩展路径不同.以β=60°为例，对圆盘的裂纹扩展过程进行分析，劈裂破坏过程见图5.当t=1.78 ms时，预置裂纹两个尖端出现损伤累积；当t=1.94 ms时，裂纹开始扩展；当t=2.06 ms时，裂纹贯通.

含不同角度预置裂纹巴西圆盘劈裂破坏过程中裂纹扩展路径的PD模拟结果与试验结果对比见图6.由此可见，本文结果与试验结果高度吻合.

2.3双裂纹巴西圆盘受对径压缩破坏

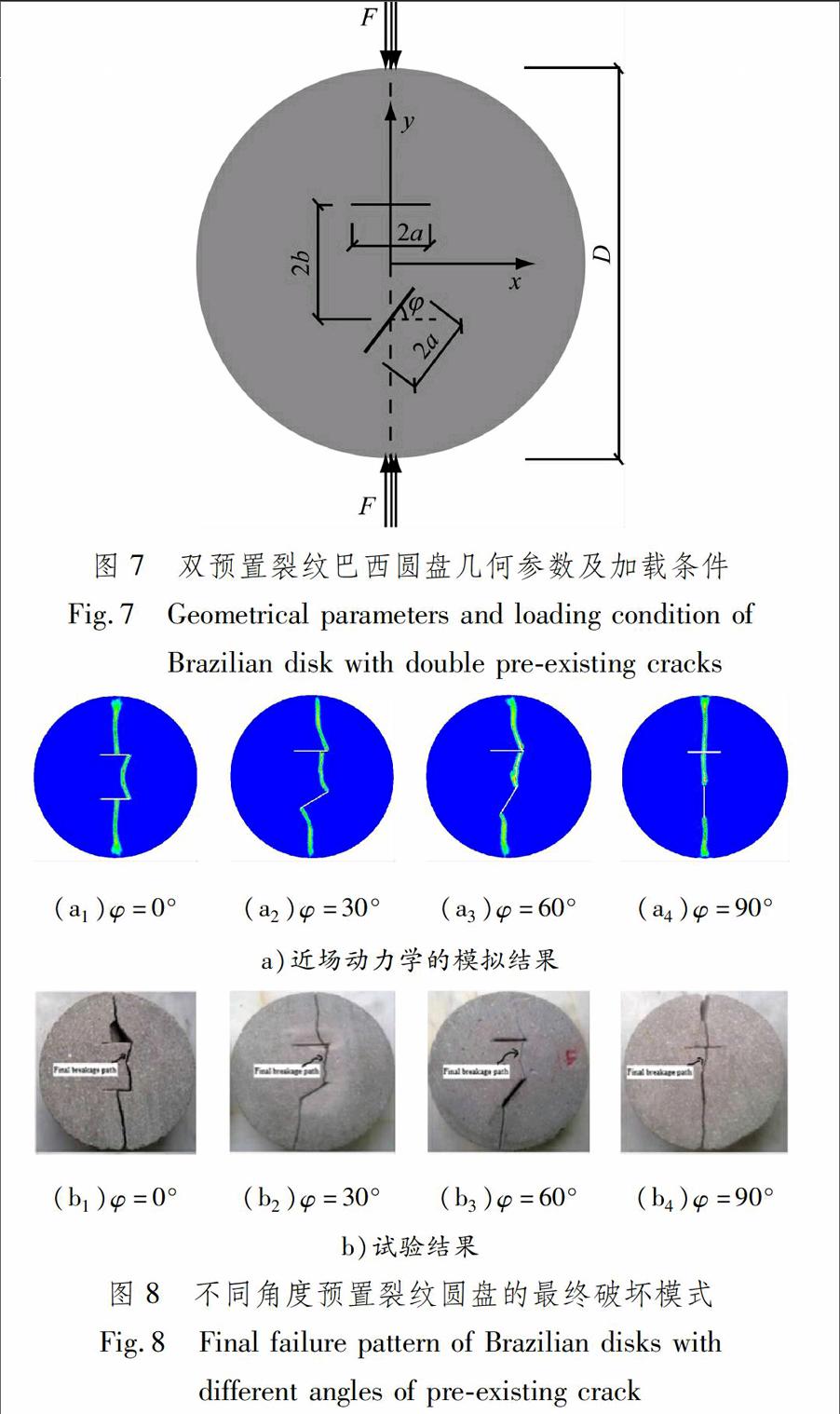
在第2.2节基础上进一步采用本文所提出的模型和算法分析含双预置裂纹巴西圆盘的劈裂破坏过程.材料参数与第2.2节一致，模型见图7.圆盘直径0.1 m，预置裂纹长度2a=0.02 m，两条预置裂纹中点间距2b=0.03 m.物质点离散间距Δx=0.000 5 m，近场范围δ=3Δx=0.001 5 m，迭代时间步长Δt=0.1 μs.分别取下方裂纹角度为0°，30°，60°和90°进行数值模拟.含双裂纹巴西圆盘劈裂破坏的裂纹扩展路径数值模拟结果与试验结果[2]对比见图8.当下方预置裂纹角度为0°和90°时，本文模拟结果与试验结果高度吻合；当下方预置裂纹角度为30°和60°时，本文模拟结果与试验结果在裂纹向下扩展的路径上稍有差异，但整体基本吻合.由此可以表明本文所提出的模型和算法能够准确模拟2条裂纹的起裂、扩展、交汇和贯通过程.

3结论

基于新興的近场动力学理论，引入动态松弛、分级加载和失衡力准则等粒子系统数值算法，构建具有较高定量计算精度且能够模拟准脆性破坏问题的PD算法体系，模拟含不同角度单预置裂纹巴西圆盘的劈裂破坏过程，所得裂纹扩展路径与试验结果高度吻合，验证本文的模型和算法.进一步采用本文方法模拟含不同角度双裂纹巴西圆盘的劈裂破坏过程，所得2条裂纹的扩展、交汇、贯通过程与试验结果吻合较好，表明本文方法适用于多裂纹脆性扩展问题，为脆性多裂纹扩展问题的高效数值模拟提供新的选择.参考文献：

[1]OUINAS D， BOUIADJRA B B， SERIER B， et al. Numerical analysis of Brazilian bioceramic discs under diametrical compression loading[J]. Computational Materials Science， 2009， 45（2）： 443448. DOI： 10.1016/j.commatsci.2008.11.004.

[2]HAERI H， SHAHRIAR K， MARJI M F， et al. Experimental and numerical study of crack propagation and coalescence in precracked rocklike disks[J]. International Journal of Rock Mechanics & Mining Sciences， 2014， 67（4）： 2028. DOI： 10.1016/j.ijrmms.2014.01. 008.

[3]钱莹， 杨军， 王兵臣. 岩石巴西圆盘动态劈裂的流形元法模拟[J]. 爆炸与冲击， 2009， 29（1）： 2328. DOI： 10.3321/j.issn：10011455.2009.01.005

QIAN Y， YANG J， WANG B C. Numerical simulation on dynamic split of a rock Brazilian disc using the manifold method[J]. Explosion and Shock Waves， 2009， 29（1）： 2328. DOI： 10.3321/j.issn：10011455.2009.01.005

[4]陈枫， 孙宗颀， 徐纪成. 单轴压缩下中心裂纹巴西试样的权函数分析[J]. 岩石力学与工程学报， 2000， 19（5）： 599603. DOI： 10.3321/j.issn：10006915.2000.05.011.

CHEN F， SUN Z Q， XU J C. Weight function solution for centercracked Brazilian disk specimen subjected to uniaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering， 2000， 19（5）： 599603. DOI： 10.3321/j.issn：10006915.2000.05.011.

[5]SILLING S A. Reformulation of elasticity theory for discontinuities and longrange forces[J]. Journal of Mechanics and Physics of Solids， 2000， 48（1）： 175209. DOI： 10.1016/S00225096（99）000290.

[6]黄丹， 章青， 乔丕忠， 等. 近场动力学方法及其应用[J]. 力学进展， 2010， 40（4）： 448459.

HUANG D， ZHANG Q， QIAO P Z， et al. A review on peridynamics method and its application [J]. Advance in Mechanics， 2010， 40（4）： 448459.

[7]刘一鸣， 黄丹， 秦洪远. 混凝土板裂纹扩展的态型近场动力学模拟[J]. 计算机辅助工程， 2016， 25（5）： 5359. DOI： 10.13340/j.cae. 2016.05.011.

LIU Y M， HUANG D， QIN H Y. Statebased peridynamics simulation for crack propagation in concrete slab[J]. Computer Aided Engineering， 2016， 25（5）： 5359. DOI： 10.13340/j.cae. 2016.05.011.

[8]郁杨天， 章青， 顾鑫. 含单边缺口混凝土梁冲击破坏的近场动力学模拟[J]. 工程力学， 2016， 33（12）： 8085. DOI： 10.6052/j.issn.10004750.2015.05.0396.

YU Y T， ZHANG Q， GU X. Impact failure simulation of a single edged notched concrete beam based on peridynamics[J]. Engineering Mechanics， 2016， 33（12）： 8085. DOI： 10.6052/j.issn.10004750.2015.05.0396.

[9]GERSTLE W， SAU N， SILLING S. Peridynamic modeling of concrete structures[J]. Nuclear Engineering and Design， 2007， 237（1213）： 12501258. DOI： 10.1016/j.nucengdes.2006.10.002.

[10]HA Y D， BOBARU F. Characteristics of dynamic brittle fracture captured with peridynamics[J]. Engineering Fracture Mechanics， 2011， 78（6）： 11561168. DOI： 10.1016/j.engfracmech.2010.11.020.

[11]KILIC B， MADENCI E. Structural stability and failure analysis using peridynamic theory[J]. International Journal of Nonlinear Mechanics， 2009， 44（8）： 845854. DOI： 10.1016/j.ijnonlinmec.2009. 05.007.

[12]沈峰， 章青， 黃丹， 等. 基于近场动力学理论的混凝土轴拉破坏过程模拟[J]. 计算力学学报， 2013， 30（S1）： 7983.

SHEN F， ZHANG Q， HUANG D， et al. Damage and failure process of concrete structure under uniaxialtension based on peridynamics modeling[J]. Chinese Journal of Computational Mechanics， 2013， 30（S1）： 7983.

[13]HUANG D， ZHANG Q， QIAO P Z. Damage and progressive failure of concrete structures using nonlocal peridynamic modeling[J]. Science China： Technological Science， 2011， 54（3）： 591596. DOI： 10.1007/s1143101143063.

[14]HUANG D， LU G， QIAO P. An improved peridynamic approach for quasistatic elastic deformation and brittle fracture analysis[J]. International Journal of Mechanical Sciences， 2015， 9495： 111122. DOI：10.1016/j.ijmecsci.2015.02.018.

[15]GERSTLE W H， SAU N， SAKHAVAND N. On peridynamic computational simulation of concrete structures[J]. ACI Special Publication， 2009， 265： 245264.（编辑武晓英）