基于粒子群算法对安全锁的结构分析与改进设计

梁才干，曾思

（1.广东中山力劲机械有限公司，广东中山528400；2.桂林电子科技大学，广西桂林541004）

设计技术

基于粒子群算法对安全锁的结构分析与改进设计

梁才干1，曾思2

（1.广东中山力劲机械有限公司，广东中山528400；2.桂林电子科技大学，广西桂林541004）

游乐场安全锁因其结构简单牢靠而广泛运用于游乐设施。基于粒子群优化算法对此机构的圆柱螺旋压缩弹簧进行优化设计，以弹簧的质量作为目标函数，以弹簧有效圈数、弹簧中径和弹簧丝直径为优化参数。设计结果表明弹簧质量明显减轻，并运用ANSYS16.0软件对其刚度进行校核。

安全锁；优化设计；圆柱螺旋弹簧；刚度

游乐场里通常会建造有过山车、摩天轮等大型设施。目前大型游乐设施正朝着高空、高速、高刺激的趋势发展，一旦安全防护措施不到位，将会造成严重的人员伤亡事故[1]。而安全锁是游乐场设施的关键部件，其结构简单，工作环境恶劣。因此对安全锁关键机构的深入分析与研究具有重要实际意义。安全锁的主要破坏原因是其弹簧的强度或刚度不够。为此本文运用粒子群优化算法对其进行优化。

1 安全锁结构分析

嫦娥奔月游乐设施的安全锁机构如图1所示，其由拉杆、螺母和圆柱螺旋压缩弹簧组成。工作原理是通过拉动拉杆压迫弹簧产生形变，完成开锁与闭锁。

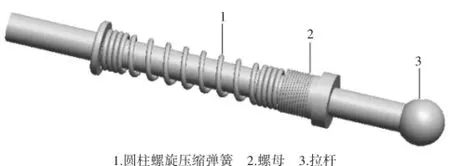
图1 安全锁机构

2 圆柱压缩弹簧优化设计

弹簧在机械产品中运用广泛，如车辆的悬挂系统、内燃机的阀门弹簧、计测弹簧等。弹簧的设计的正确与否决定着设备的安全性能。为了对弹簧进行优化设计，刘仪山等人[2]建立起了弹簧的数学模型，并把弹簧约束条件分为了性能约束和边界约束。张信群[3]则是运用面向对象的方法开发出弹簧自动化建模界面，提高了优化设计的效率。Kaoua等人[4]为了揭示在拉伸载荷下双螺旋弹簧的受力情况，建立了有限元素质模型并发现单股弹簧丝的最大应力分布在于其自旋角度为180°处。Amin等人[5]则是建立了两端固定圆柱螺旋弹簧的有限元模型，并对其不同参数条件下对其的形变和固有频率进行分析。韩泽光等人[6]对内燃机气门压缩弹簧进行优化设计时，分别选取了最小重量，最大刚度和最大强度为目标函数进行了优化。本文则基于PSO算法对弹簧进行优化设计得出最优的结构。

2.1 目标函数

压缩弹簧的目标函数有很多，对于本文的压缩弹簧，选取以质量为最小为最优化设计目标。

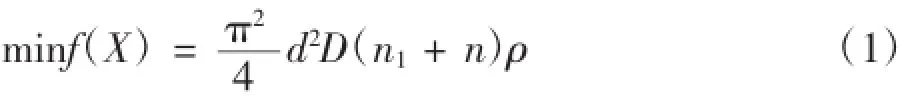
式中，n1为弹簧的支撑圈数，取n1=4.

2.2 约束条件

（1）最少工作圈数约束

为了避免由于载荷偏心引起过大的附加力有效工作圈数n应约束如下：

g（1）：4≤x1≤20

（2）旋绕比约束

旋绕比C值愈小，曲率越大卷制约困难，弹簧的刚度也越大。该约束条件为：

g（2）：4≤x2/x3≤10

（3）弹簧中径约束

根据圆柱弹簧的实际使用环境知，弹簧的中径D必须限制在一定的范围内，故其约束为：

g（3）：10≤x2≤26

（4）弹簧丝直径约束

根据弹簧钢丝产品从而得到弹簧丝直径约束条件：

g（4）：1.2≤x3≤2.5

（5）刚度条件

弹簧刚度应满足形变要求，所以：

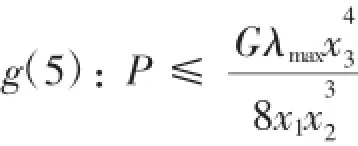
式中，λmax为弹簧的最大压缩变形量；G为弹簧材料的切变模量；P为工作载荷。

（6）强度条件

为了保证弹簧工作时在最大工作载荷作用下，弹簧不产生永久变形应满足：

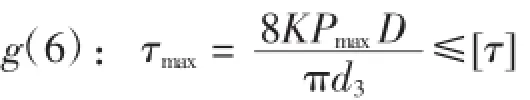
式中，Pmax是最大的工作载荷，为50 N；K为弹簧曲度系数；[τ]为许用应力。本文弹簧材料为65Mn，为2类载荷弹簧。

3 粒子群算法

1995年由美国社会心理学家James Kennedy博士电气工程师Russell Eberhart博士[7]提出了粒子群算法。其基本概念源于对鸟群和鱼群捕食行为简化社会模型的模拟。利用待优化问题的目标函数的值的优劣来判断每个粒子性能的优劣。通过m个粒子的迭代运算以获得问题的全局最优解。在每一个粒子的每一次迭代时，两个极值分别是个体极值pbx和全局极值gbx来更新自己的位置和速度。

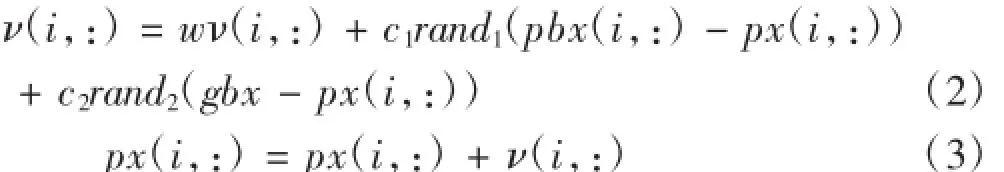
式中，C1=C2=2是学习因子；rand1和rand2是[0，1]上的均匀分布的随机数；W是惯性权重值，是由YuShi Hui[8]提出来。

4 优化方法与优化结果

设置其迭代次数为150，粒子数为25，惯性权值值从0.8衰减到0.4.结果如图2所示，各优化参数值为X0=[14.673 2 18.018 9 1.793 8]T.经圆整为X=[15 18 1.8]T，优化后的弹簧质量为20.9 g.

图2 粒子群优化结果

5 有限元分析

5.1 刚度校核

圆柱螺旋压缩弹簧刚度的理论值公式如下

此弹簧用65Mn钢制成，把优化后的弹簧几何参数代入式（4），弹簧的理论刚度K=1.185 N/mm.通过建立起了有限元仿真模型并获得方向力上的形变如图3所示。根据仿真出的弹簧形变，基于弹簧刚度的计算公式F=kx，获得弹簧刚度为1.276 N/mm.与理论刚度值的相对误差为7.7%，符合工程计算精度。其在最大载荷下的应力分布图如图4所示。由图可知弹簧的最大应力值为88.382 MPa.远未达到65Mn钢的屈服强度。可见优化后的弹簧满足强度的要求。

图3X轴形变

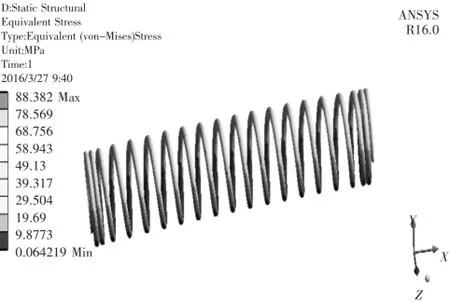
图4 应力分布

6 结束语

本文运用粒子群优化算法对安全锁的圆柱螺旋压缩弹簧进行优化。在充分考虑了此弹簧的工作环境下建立起了以弹簧质量作为评价弹簧性能优劣的目标函数。优化结果发现：当弹簧有效圈数为15，弹簧中径为18.0 mm，弹簧丝直径为1.8 mm时，此压缩弹簧满足工作需求同时重量最轻。并对刚度校核，发现理论刚度与模拟刚度值的误差在10%内，验证了模型的正确性和弹簧的安全性。相比于常规方法大大缩短产品的设计周期同时避免求解工程中陷入局部解，为机械零件优化提供了新的优化方式。

[1]张煜，张新东，李向东，等.我国大型游乐设施风险分析研究[J].中国安全生产科学技术，2013，9（9）：160-164.

[2]刘义山，李骥昭.普通圆柱螺旋弹簧的优化设计数学模型[J].机电产品开发与创新，2010，23（5）：23-24.

[3]张信群.圆柱螺旋压缩弹簧参数化建模[J].机电工程，2011，28（3）：305-309.

[4]Sid Ali Kaoua，Kamel Taibi，Nacera Benghanem，et al.Nu merical Modelling of Twin Helical Spring under TensileLoad ing[J].Applied Mathematical Modelling，2011（35）：1378-1387.

[5]Aimin Yu1，Changjin Yang.Formulation and Evaluation of an Analytical Study for Cylindrical Helical springs[J].Acta Me chanica Solida Sinica，2010，23（1）：85-94.

[6]韩泽光，费烨，郑夕健.基于多目标遗传算法的圆柱螺旋压缩弹簧方案设计[J].中国制造业信息化，2006，35（3）：27-30.

[7]J.Kennedy，R.Berhart.Particle Swarm Optimization[C].Proc eedings of IEEE International Conference on Neural Net works，1995（4）：1942-1948.

[8]Shi Y，Ebethart R.C，A Modified Optimizer[C].Proceedingsof the IEEE Congresson Evolutionary Computation，1998：69-73.

Structural Analysis and Improvement of Particle Swarm Algorithm Based on Security Lock

LIANG Cai-gan1，ZENG Si2
（1.Guangdong Zhongshan Heavy Industry Co.，Ltd.，Zhongshan Guangdong 528400，China；2.Guilin University of Electronic Technology，Guilin Guangxi 541004，China）

The playground safety lock because of its simple structure，reliable and widely used in recreational facilities.In this paper，based on particle swarm optimization algorithm to optimize the design of cylindrical helical compression spring.Taking the spring mass as the objective function，the effective number of spring，the diameter of spring and the diameter of spring wire are the optimal parameters.The results show that the quality of spring is lightened，and the stiffness is checked by ANSYS16.0 software.

safety；optimization design；cylindrical spiral spring；stiffness

TH135

A

1672-545X（2017）03-0005-03

2016-12-29

国家自然科学基金（编号：51566002）

梁才干（1981－），男，广西平南人，大专，主要从事游乐设备品质管理；曾思（1992－），男，广西南宁人，硕士研究生，研究方向为传热与流动、发热设备热控技术。