小学应用题解答能力的培养

四川省德阳市罗江县鄢家镇小学校 范 匀

小学应用题解答能力的培养

四川省德阳市罗江县鄢家镇小学校 范 匀

小学生应用题解答能力的培养，应把培养学生正确分析数量关系作为关键，以培养学生的思维能力为途径，从低年级开始要求学生养成审题和验算习惯，抓住联想训练、对比训练、编题训练、一题多问和多变训练等方法入手来实现培养学生解答应用题的能力。

应用题；解答；能力；培养

应用题是根据日常生活和生产中的具体事实，用语言或文字表示数量关系的问题，它是小学数学教学的一个重点和难点，在教学中占有十分突出的位置。应用题教学既能加强学生数学学习和现实生活的联系，又能强化学生的数学基础知识，还能培养学生的思维能力。在学生应用题解答能力的培养上可从四个方面入手。

一、要特别重视培养学生分析数量关系的能力

应用题都是由已知条件和问题两部分构成的，教师要在学生解答应用题的思考过程中，让学生能逐步舍弃其中具体的生产、生活情节，将其中的数量关系概括、抽象为数学问题，这是正确解答应用题的关键。抽象为数学问题其实就是正确理解应用题的数量关系，它是在对数学基础知识牢固掌握的基础上，加强对加减乘除四则运算意义的理解，能把题目中表述的数量关系与四则运算的意义密切联系，教学中要特别注意引导学生分析数量关系与四则运算之间的联系，从而使学生学会正确分析应用题中的数量关系。

复合应用题都可看成是由简单应用题组成的，学生只要能掌握简单应用题的结构、条件和问题之间的相互关系，那么学生解答应用题就有了钥匙。简单应用题是根据加减乘除的意义解答的一步应用题，教学生正确理解简单应用题的数量关系，是培养学生学会分析数量关系的重要途径之一。教学简单应用题要注意使学生掌握其结构，弄清题目中条件与条件、条件与问题之间的关系，紧扣四则运算的意义，分析概括出应用题的数量关系。

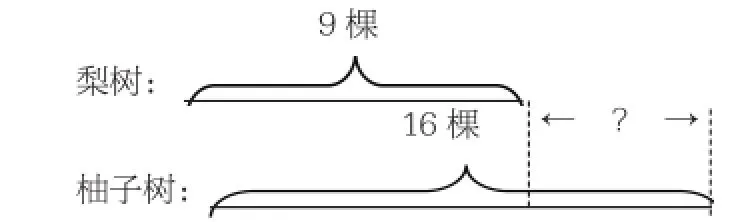
通过图学生认识到本题是16棵柚子树和9棵梨比多少，16棵柚子树可分成两部分，即与梨树同样多和比梨树多的部分。引导学生掌握它们的关系，从柚子树的棵数中去掉与梨树同样多的9棵，剩下的就是柚子树比梨树多的棵数。这样，题中的数量关系转化成从一个数中去掉一部分，求另一部分，直接反映了减法的运算意义，即：16-9＝7（棵）。

又如：小张家栽了9棵梨树，比柚子树少栽7棵，柚子树有多少棵？要引导学生先理解题意分析：梨树比柚子树少栽7棵，柚子树棵数是标准数，而这个数是未知数，就要理解为“柚子树比梨树多7棵”，进一步理解：柚子树和梨树同样的棵数与柚子树比梨树多的棵数合并起来，就可以求出柚子树的棵数，这道题中的数量关系转化成把两个数合并成一个数，揭示了加法运算的意义，即9+7＝16（棵）。

因而，教师在教学简单应用题时，要花时间、花力气对学生严格要求，严格训练，加强简单应用题数量关系的分析，在此基础上，训练学生逐步提高分析数量关系的能力，适时把日常生活生产中常见数量概括为数学术语，比如：“速度、时间、路程”“单价、数量、总价”“工作效率、工作时间、工作总量”等等，这样逐渐提高学生分析数量关系的能力，为正确解答应用题解决关键问题。

二、要有意识地培养学生分析推理的能力

小学生的推理能力是随着学生年龄增长和掌握的知识经验而形成和提高的，他们先是具有一定的直接推理能力，然后才形成间接推理能力，在解应用题中，间接推理应用得更多。利用“一题多解”应用题的教学，是培养学生间接推理的一种好方法，使学生能逐步抓住问题的本质，根据思维对象、材料特征、类型加以灵活运算，就能产生较多的思维起点，分析综合思路逐步开阔，达到培养学生分析推理能力的目标。

例如：光明小学6年级3班有学生45人，女生数是男生数的，男、女生各有多少？

方法二：把45人平均分成15份，其中女生占7份，男生占8份，那么男生数：45÷（8+7）×8＝24（人），女生数：45÷（8+7）×7＝21（人）。

经常通过一题多解的训练，使学生从不同角度、不同方位、应用不同的知识解决问题，实现对应用题的判断、处理、选择，从而让学生掌握分析、综合等逻辑推理方法，在发散性、多角度的思维活动中实现推理能力的培养。

三、要抓好培养学生会审题和验算的能力

解答应用题的基石是学生学会审题。审题其实就是读懂题，弄清题意，教学时要特别注意对学生审题能力的培养，从低年级就要开始培养学生认真读题的习惯，做到不添字、不漏字，逐字逐句，逐符号阅读，边读边记边理解，通过读题，弄清题目讲什么事，有哪些已知条件，求什么问题，条件与条件、条件与问题间的联系等。对题目中的重点词句，要引导学生充分理解这些关键词在题目中的含意，有的题还要抓住关键句画图进行分析，为分析解答应用题奠定基础。

通过微气象站数据采集模块和在线模拟数据采集模块，每3 min采集1组数据，总共采集10组数据，根据所采集的10组数据建立GM(1,1)模型。根据GM(1,1)模型预测未来12 min内的风速、降雨量、液态水含量，通过所预测的风速、降雨量、液态水含量预测未来9 min内的覆冰增长状态。具体方法如下。

在教学生理解题意时，注意排列条件，对条件较隐蔽、叙述简练的应用题还可以通过将词语补充完整，从整理条件中发现一些隐蔽关系，从而找到解题的线索。当然，还要让学生注意单位名称，看条件之间、条件与问题之间的单位名称是否一致，有时，题目中“保留几位小数”、“用方程解”、“用几种方法解”等内容也不能忽视。

应用题验算是让学生学会自己判断解答方法对不对，计算正确不正确，教师在日常教学中要引起足够重视，让学生养成验算的习惯是解答应用题必不可少的环节。验算一是用估算的方法，看计算结果符不含合题意、符不符合现实生活；二是把计算结果作为已知条件，把应用题其中的一些条件当成问题，看解答结果是否一致；三是用“一题多解”的方法，看不同方法解答是不是完全一样，若一样，则说明解题是对的，若不一样，就要查找问题。用验算既能培养学生的逻辑思维，又让学生自己判定应用题解答是否正确，实现验算的作用，经过长期的培养，使学生养成良好的解答应用题的习惯。

四、要抓住多角度训练，提高学生解决问题的能力

练习解应用题是学生巩固知识，形成技能，发展思维能力的必要途径，因此，教师要善于通过多角度训练来提升学生解决问题的能力。

1.要抓好联想训练

“联想”是指看到眼前事物而想到相关联的另一些事物，它是一种积极的思维活动。例如：修一条水渠，已修了，可以联想到：（1）水渠还剩未修；（2）已修的比剩下的这条水渠多（3）剩下的比已修的这条水渠少（4）已修的是剩下的倍；（5）剩下的是已修的（6）已修的比剩下的多（7）剩下的比已修的少（8）把这条水渠平均分成9份，已修的占5份，剩下的占4份；（9）已修的与未修的比是5∶4；（10）未修的和已修的比是4∶5；（11）已修的和水渠全长比是5∶9；（12）剩下的和水渠全长比是4∶9。

2.要强化对比训练

有些互相联系的知识学生容易发生混淆，为了揭示它们之间的内在联系，让学生同中见异，异中见同，可以变换条件，强化对比训练。如：小明家果园有：

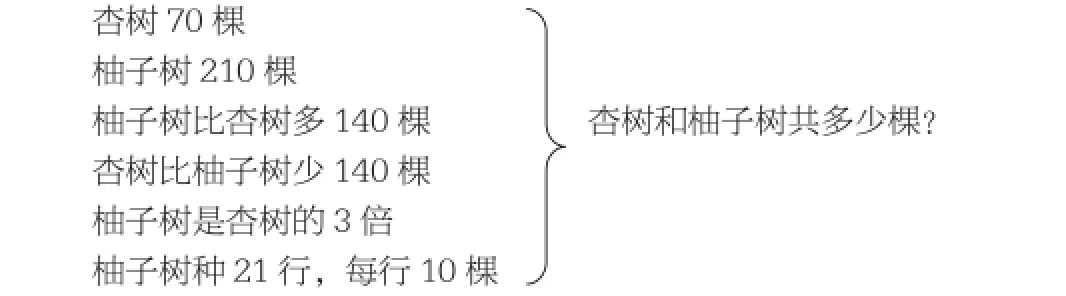
不管题目怎样变，解法不同，但基本数量关系是相同的，即：杏树棵数+柚子树棵数＝共多少棵。

3.要利用好编题训练

编题训练能帮助学生自己进一步弄清应用题的数量关系，熟练掌握应用题的结构特征，提高对应用题的理解和解答能力，同时，还可以培养学生的语言表达能力。编题训练的方式很多，有看图编题，看实物编题，根据算式编题，给两个数编题，用生活实际编题等等。

4.要重视一题多问训练

一题多问是培养学生发散思维的一种好方式，如：一条路560米，第一天修了全长的第二天修了全长的，可以提出下列问题：（1）第一天修了多少米；（2）第二天修了多少米；（3）还剩多少米未修；（4）两天共修了多少米；（5）第二天比第一天多修全长的几分之几；（6）第一天比第二天少修全长的几分之几；（7）还剩几分之几没修；（8）已修的比没修的少多少米；（9）没修的比已修的多多少米……

通过这种训练使学生认识到，在条件相同的情况下，不同的问题有不同的解题思路和解答方法，从而提高学生分析问题、解决问题的能力。

5.要突出一题多变的训练

设计一题多变的练习题，使学生通过练习抓住题中的本质，提高学生的应变能力和融会贯通的能力。如：两辆车从甲、乙两地相对开出，甲车平均每小时行60千米，乙车每小时行56千米，（1）经过4小时两辆车相遇，甲、乙两地相距多少千米？（2）经过4小时两车还相距120千米，甲、乙两地相距多少千米？（3）如果甲先开出1小时，乙车才开出，行了4小时两车相遇，甲、乙两地相距多少千米？（4）如果甲车开出后中途停留半小时，4小时后两车相遇，甲、乙两地相距多少千米？

这一组题根据条件分析，都要用到同一个关系式：速度×行驶时间＝路程，（60+56）×4＝464（千米），需要学生思考：464千米是不是就是以上各题中所要求的甲、乙两地距离？为什么？如果不是，应该怎样求？从而促使学生弄清题目的本质特征，在掌握相遇问题的基本数量关系的基础上掌握各种变化的情况。

总之，培养学生应用题解答能力需要教师根据学生的年龄特征，利用学生思维发展特性，抓住正确分析应用题数量关系这一关键，从培养学生良好的审题习惯入手，抓住多角度训练途径，对学生加强方法指导，经过长期的培养来提高学生解决问题的能力。