浅谈求函数最值的方法

江苏省张家港高级中学 张新秀

浅谈求函数最值的方法

江苏省张家港高级中学 张新秀

最值问题是历年高考重点考查的常见题型。由于其综合性强，能力要求高，解决这类问题要灵活选择恰当的解题方法。求最值的方法有很多种，教学中我感受到不必追求新颖别致、灵活奇巧，应该集中精力练好几种常用方法，努力打好基本功，自然能够得心应手。

一、反解法

当已知自变量或者某个因式整体的范围时，反解法能够快速准确地求出函数值域。

二、换元法

把某一部分看作一个整体或用一个新元来代替,能够达到“看起来熟悉、用起来顺手、写起来简洁”的目的。

运用换元法时应特别注意引进的新元的取值范围，这是一个易错点。

三、函数单调性法

求函数值域，应该让学生养成先观察函数在定义域上的单调性的习惯，这往往能够快速找到解决问题的切入口。

若函数在整个区间上不是单调的，则先研究函数单调性，把该区间分成各个小区间，使得函数在每一个区间上是单调的。

四、基本不等式法

基本不等式在求范围或值域问题中往往显得非常活跃，当其形状结构不太明显时，常常借用换元法、配凑法等手段以达到凑形的目的。

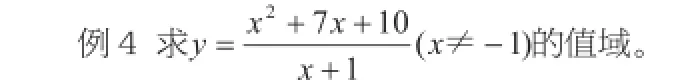
解：本题看似无法运用均值不等式，但经过配凑之后便可呈现出基本不等式的形态。g(x)恒正或恒负的形式，然后运用均值不等式来求最值。运用基本不等式求最值,应注意“一正二定三相等”三个条件缺一不可。当不能确定主变量为正数时应该分情况讨论。

五、判别式法

对于二次分式函数的值域问题，可以用方程的思想先将函数化为方程的形式, 再利用一元二次方程有根的条件求解。

判别式法求值域往往局限于二次函数，而且一定要关注二次项系数为0的情形。

求函数最值的方法还有很多，比如导数法在求最值方面比其他方法的适用范围都要广泛，尤其是超越函数或者混合函数中导数的优越性无可替代。这里不再赘述。

数学（包括几何）有分量的问题最后往往都和函数的最值有关，教学中我们要重视求最值的方法的训练和提炼，但无须刻意追求灵巧新奇，以常见的基本方法为主，相信熟能生巧，基本功扎实了，自然能够得心应手。