合成超硬复合体原料的状态方程及应用

冯吉福，林 峰 ，李立惟 ，何绪林

(1. 广西超硬材料重点实验室，广西 桂林 541004；2. 国家特种矿物材料工程技术研究中心，广西 桂林 541004；3.中国有色桂林矿产地质研究院有限公司，广西 桂林 541004)

合成超硬复合体原料的状态方程及应用

冯吉福1,2,3，林 峰1,2,3，李立惟3，何绪林3

(1. 广西超硬材料重点实验室，广西 桂林 541004；2. 国家特种矿物材料工程技术研究中心，广西 桂林 541004；3.中国有色桂林矿产地质研究院有限公司，广西 桂林 541004)

基于CASTEP的第一性原理方法, 研究了六面顶压机高压腔体常用组装材料在30GPa以内的压力与晶胞参数关系，给出了超硬材料工程压力范围内(3～10GPa)的常用材料的布里奇曼状态方程。以0℃～1800℃、高压下氯化钠的压力-体积实测数据，进行了布里奇曼状态方程的拟合，讨论了状态方程在合成金刚石复合片条件下的有效性。利用材料的布里奇曼方程和高压腔体中组装材料的压缩率，进行组装材料的体积和结构的设计，在相同表压的条件下，实现了高压腔体内压力的明显提高。在六面顶压机上进行了合成了金刚石/硬质合金复合体试验，验证了这种设计方法的可靠性。

计算材料学;状态方程;高压腔体;组装

六面顶压机是中国发展的超高压工业设备，主要用于合成人造金刚石和立方氮化硼及其复合材料。通常在工业应用中，在额定表压下，高压腔体实际压力处于5GPa～6 GPa之间，虽然根据增压方式理论计算的压力可达10GPa，所以实际压力传递压效率不高。对合成金刚石及立方氮化硼的复合片，较高的压力可以提供更大的工艺范围，且对金刚石、立方氮化硼复合片的质量也有提升。因此提高六面顶压机高压腔体的压力，同时保持更大的有效腔体一直是超硬材料工作者的重要工作[1-3]。

虽然高压下的物态研究进行了上百年，高压下的物态方程和模型研究也有很多，但是在合成超硬材料上常用的组装材料的高压下的状态方程研究却不多。因此，研究超硬材料工程常用材料的物态方程，如布里奇曼状态方程的简单形式，可方便用于在超硬材料行业中，对提高六面顶压机高压腔体压力的设计、提高压力传递效率是比较有意义的。

1 研究方法

1.1 常用组装材料的压力与体积研究方法

采用第一性原理的计算方法进行高压下物质状态的研究，根据压力与体积关系，拟合得到压缩率-压力的布里奇曼状态方程。首先，根据研究材料的晶体结构建立计算模型，然后由MS-CASTEP模块计算。CASTEP(Cambridge Sequential Total Energy Package)是一个基于密度泛函、平面波、赝势理论的从头算量子力学程序[4]。在给定压力下，计算模型中各原子受力处于平衡状态，使之能量处于最低，从而优化结构，进而得到合理的结构。CASTAP的计算基于减小计算力和应力的数量级，直到小于规定的收敛误差，也可给定外部应力张量来对拉应力、压应力和切应力等作用下的体系行为模型化，在这些情况下反复迭代内部应力张量直到与所施加的外部应力相等，得到受力平衡时模型的各原子位置参数，通过这些位置数据得到晶胞参数。

CASTEP研究中, 所用赝势为:碳2s2 2p2、 钠2s2 2p6 3s1、氯3s2 3p5、铝3s2 3p1、硅 3s2 3p2、 氧 2s2 2p4、镁 2p6 3s2、钙 3s2 3p6 4s2、钨5s2 5p6 5d4 6s2、 钴 3d7 4s2、铁3d6 4s2、硼2s2 2p1、氮s2 2p3等，电子相关效应采用广义密度近似，电子状态方程采用数值求解(积分点数FFT mesh=36×36×36)，k-point 间距为0.04 (Å-1)，计算参数设置如表1所示，组装材料模型的结构主要参数如表2所示。

表1 计算参数设置

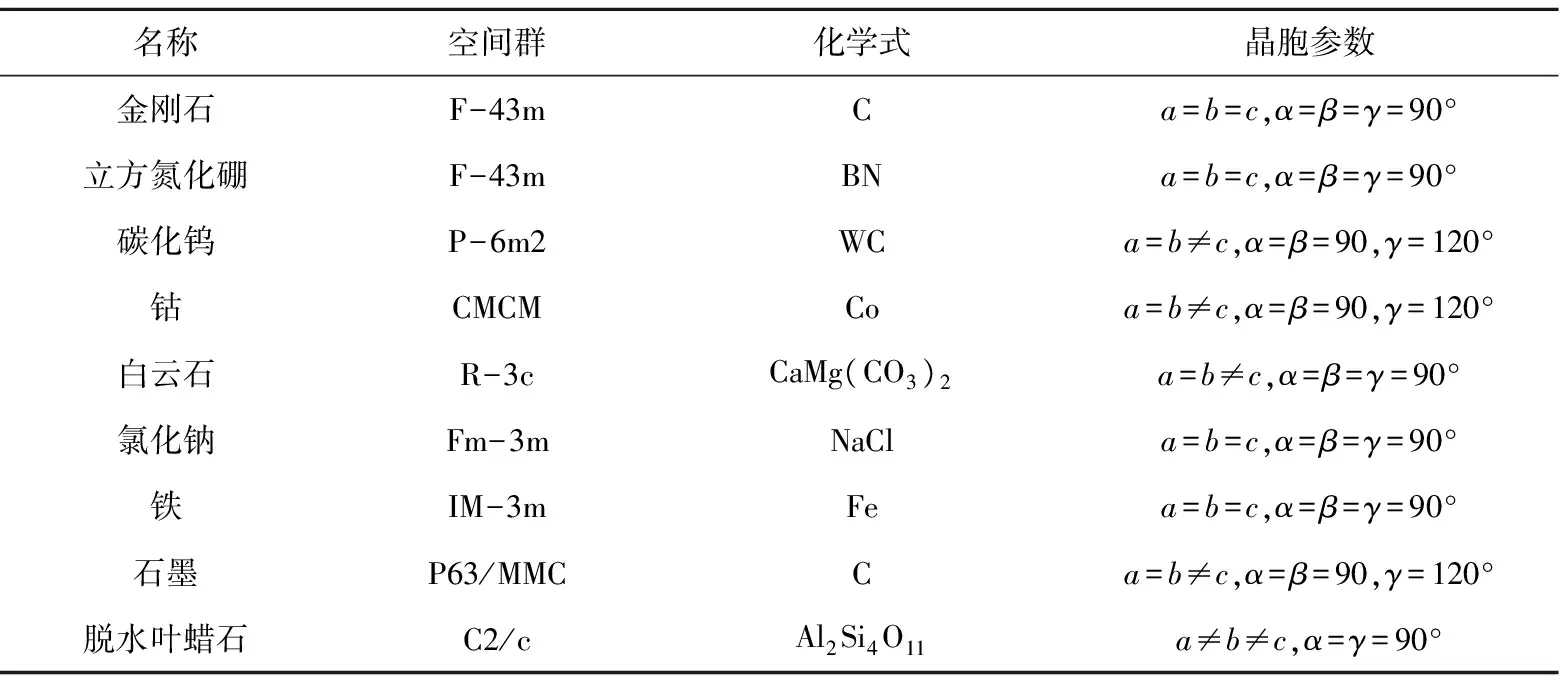
表2 材料的结构模型

1.2 状态方程应用

对高压腔体设计研究和验证的试验工作在CSⅡ六面顶金刚石液压机上进行。根据材料的布里奇曼状态方程，结合组装材料在组装状态下的致密度，通过高压腔体中的材料的压缩率设计组装体积，并进行试验验证。试验中所使用的材料均为工业材料，使用天平在测得组装元件质量的同时用千分尺测得尺寸算出材料的密度，以所测密度与理论密度之比作为致密度。

2 结果与分析讨论

2.1 模型优化结果

第一性原理的计算由模型结构决定波函数的周期性，模型是否符合事实，对计算结果在工程中能否实用起决定作用。研究使用的叶蜡石的模型是根据《叶蜡石的密封性能》[5]的结构建立，文献中没有水的占位，因此本研究的模型是脱水的叶蜡石。真实的叶蜡石完全脱水一般在500℃～800℃的条件下，实际生产中只有部分厂家的叶蜡石的焙烧达到完全脱水的温度，此外真实的叶蜡石含有众多的杂质和类质同象的原子取代。因此叶蜡石模型可能与部分厂家的性能有差别。叶蜡石晶格[6]为a0=0.515nm，b0= 0.892 nm，c0=1.895nm，β=99°55′，密度为2.79，若叶蜡石脱水后晶格不变密度应当为2.64，脱水叶蜡石模型计算的密度2.42，计算表明叶蜡石脱水膨胀，符合实际的事实。叶蜡石焙烧后的传压性能更好，所以用脱水叶蜡石可以作为叶蜡石的压力-体积状态的典型代表。其他材料均使用经典的结构建立模型[6]，零压力下的计算结果与Jade5.0中数据库的标准PDF卡片值比较，如表3所示。

表3 材料晶胞参数的优化计算结果与标准值(×10-10m)

表3的结果表明，金刚石、立方氮化硼、碳化钨等硬质材料计算值与实验值保持高度一致，石墨、氯化钠等在自由压力时晶胞参数变化大的模型，与标准卡片有出入，考虑计算压力收敛标准为0.1GPa，即计算得到零压力下晶胞参数结果与零压力可能存在±50MPa的静水压差，所以认为优化计算结果与事实相符。因此，认为研究的高压腔体组装材料模型准确，得到的不同压力下的状态可以代表真实材料的状态。

2.2 零度下的状态方程

根据计算的结果，绝对零度下、不同压力下晶体的晶胞参数如表4至表7所示。

由晶胞参数求出晶体体积，拟合成布里奇曼状态方程。在研究中发现，仅在一定压力范围内可以用布里奇曼形式的状态方程准确描述。为了适应金刚石和立方氮化硼复合片的合成需要，在外推压力为0时与研究结果对应，同时在3～10GPa下，状态方程准确，各种材料的布里奇曼状态方程列于表8。

表4 在不同压力下的主要晶胞参数(×10-10m)

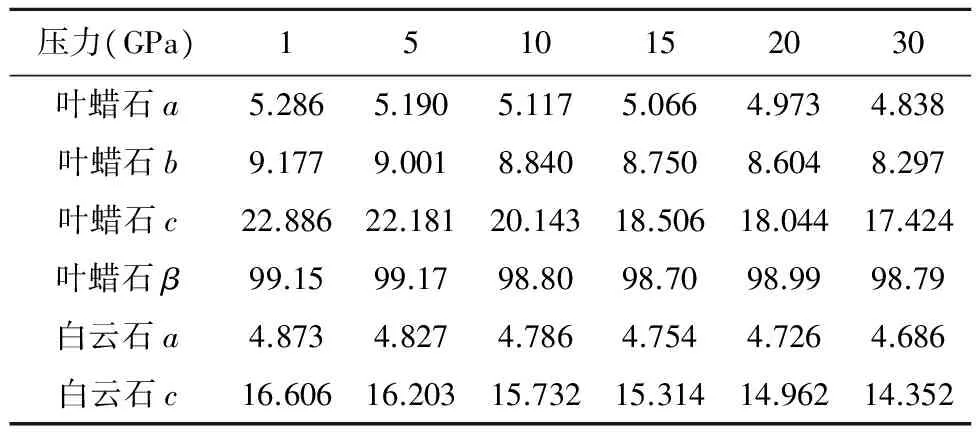
表5 不同压力下叶蜡石晶胞参数(×10-10m)

表6 不同压力下的铁和氯化钠晶胞参数

表7 不同压力下的石墨晶胞参数

表8 常用材料的布里奇曼状态方程

2.3 高温下的状态方程

据理想晶体热压pT与比容非相关的假定[7]，可以直接由0 K的状态方程计算相应的热压。0 K和温度为TK的温等温物态方程分别表示为p(0，v)和p(T，v)。当v=v0时，p(T，v0)=0。所以pT(T)=p(T，v0)-p(0，v0)=-p(0，v0)。则T温等温物态方程可以写为：

(1)

由式(1)可见如果晶体的状态方程能描述低温下状态，高温下的等温状态方程与低温下方程形式基本相同但相差一个常数，常数为-p(0 K，v0)。

当研究的物质为非晶体，或者高温下物质发生了相变，超出了式(1)的适用范围。根据托马斯-费米模型的理论认为高压下的压力-体积关系与单位体积内的电子有关(忽略了原子核热运动产生的热压)，与点阵结构无关[8]。因此，研究的对象在高压高温下产生固液相时，相变时单位体积内的电子变化轻微，高压下液态的状态方程能够用该物质高压晶体状态方程近似描述。表9列出了文献[9]中氯化钠在不同温度下的压力与体积实测数据为基础的拟合布里奇曼状态方程系数，由于25℃之外的数据是压力下的数据，其自由体积使用的是外推的布里奇曼方程外推自由体积，在20 GPa压力下范围内，不同温度的布里奇曼方程的一次项系数和二次项系数(压力以GPa为单位)如表9所示。

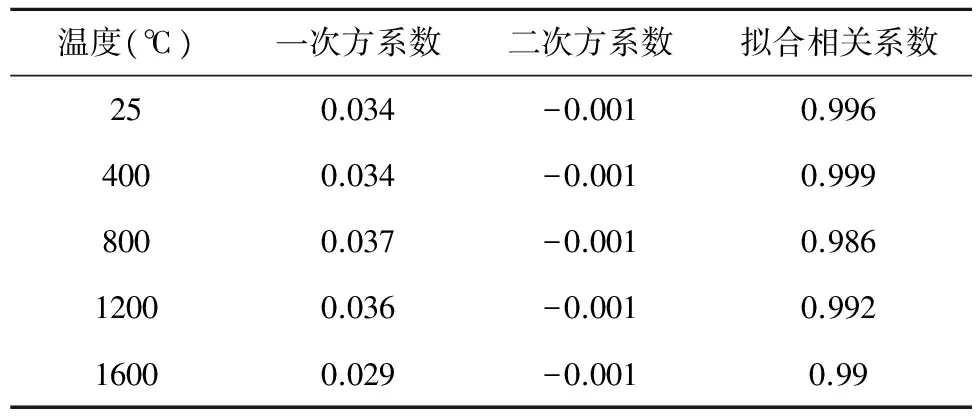
表9 氯化钠的布里奇曼状态方程系数

对比实测试验数据和计算结果的氯化钠的布里奇曼状态方程，方程中a、b平均值分别为0.034、-0.001和0.033、-0.0008，两者相当一致。

通过对氯化钠计算得到的状态方程和实测状态方程的比较，确认了在30GPa压力范围内液态氯化钠可用固态氯化钠的状态方程如式(1)的方式近似描述。在六面顶压机合成金刚石(立方氮化硼)复合片中钴也可以发生固液相变，也可用固态状态方程如式(1)的方式近似。

2.4 组装材料在合成状态下的压缩率

构成高压腔体的材料是在常温下进行组装的，而合成反应温度约1500℃，因此，利用状态方程计算材料的初始体积，要考虑温度变化发生的体积变化，应以组装尺寸变成合成温度下的体积(下称组装体积)作为初始体积。温度升高至1500℃时，氯化钠发生固液相变，体积膨胀到0K固体的1.6倍[10]，根据热膨胀系数计算，硬质合金、钴、铁体积膨胀大约膨胀1.05倍，叶蜡石还是处于较低的温度，因此认为叶蜡石从组装到反应状态下没有体积变化。完全致密的理想材料，且不考虑温度变化的，压力在5.5GPa下体积压缩率列入表10中。在合成金刚石/立方氮化硼复合片工业生产中，实际材料是粉末状或粉末状制备，其致密度小于1，高温状态和5.5GPa压力下，实际材料的压缩率与致密度一并列入表10中。

表10 理想材料和实际材料在5.5GPa下的体积压缩率

根据文献[11]，在六面顶压机超压形成高压腔体的时候，组装材料被压缩，而最终由形成高压腔体积的“临界体积”决定。“临界体积”与组装体积之比，决定了材料的压缩率。根据材料的状态方程，压缩率和压力是对应的，因此，压缩率决定了合成腔体的压力。根据“临界体积”和材料的状态方程设计组装材料的体积，可提高合成状态下腔体压力。

由表10可知，致密度导致理想材料和实际材料的压缩率变化非常大。叶蜡石压缩率大于白云石压缩率，作为传压介质的叶蜡石和白云石，它们同时占据了高压腔体大部分体积，白云石更有利于腔体压力提高。氯化钠的固液相变，使组装体积发生较大的变化，抵消了致密度不足的缺点，是良好的组装材料。

2.5 状态方程在高压腔体组装设计中应用

某公司的六面顶压机合成金刚石/硬质合金复合片，成品率低于50%，绝大部分废品的原因是复合体中心出现凹点，经分析认为，压力不足是主要原因。根据高压腔的体积和压力，计算出构成组装腔体的材料压缩率，再得到组装材料的组装体积，据此思路对高压腔体组装重新设计，目标是高压腔体平均压力超过5.5GPa。

试验工作在Φ320mm压机上进行，其标准块为34mm，叶蜡石边长37.5mm，高压腔体体积40000立方毫米。高压腔体组装由叶蜡石，堵头等组成，如图1所示。改进后组装外形尺寸与以前保持一模一样，使用减少石墨用量、提高使用氯化钠比例等手段，高压腔体体积与组装体积确定的压缩率由26.6%变成了23.7%。在压力标定试验中，用原来组装结构，表压90MPa，测不到5.5GPa钡的相变点，重新设计组装后，可以测到5.5GPa钡的相变点。改进后金刚石/硬质合金复合片成品率超过80%，复合片微观结果如图2所示，复合片的应用性能优良[12]。

应当指出，这样设计组装腔体，没有考虑化学反应形成体积变化，不过在合成超硬材料中化学反应通常只在界面发生，相对量较小，实验表明这样的设计过程结果可行，可用于六面顶压机高压腔体压力设计。

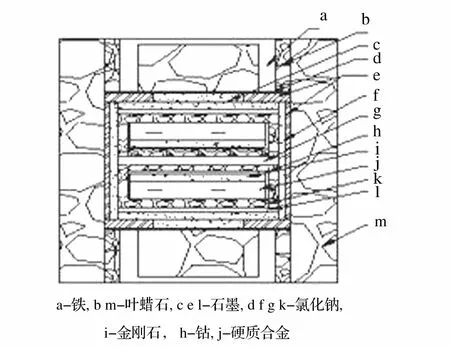
图1 组装结构示意图Fig.1 Schematic diagram of assembly structure

图2 金刚石/硬质合金复合体Fig.2 Diamond/ cemented carbide composite

3 结语

基于第一性原理计算得到的常用六面顶压机高压腔体组装材料压力体积状态信息，在3～10 GPa压力范围内，常用组装材料可拟合成布里奇曼形式，对合成金刚石/立方氮化硼复合片高压腔组装设计具有实用价值。组装材料致密度不足是导致高压腔压力不足的重要原因。采用氯化钠作组装材料，利用高温下固液变化产生的体积膨胀，可以有效提高高压腔体的压力。

[1] 徐祖全,李侃平,孙璇,等.国产六面顶压机的精密化发展[J].超硬材料工程, 2011, 23(4)：43-46.

[2] 方啸虎,谢德龙,万隆,等.我国超硬材料的今天和明天[J].超硬材料工程, 2013,25(2)：38-42.

[3] 罗锡裕,刘一波,徐燕军,等.挑战加工金属材料用超硬材料工具[C].北京：粉末冶金产业技术创新战略联盟论坛论文集,2010：147-157.

[4] 原鹏飞.第一性原理方法计算几种材料高压下的相变和弹性性质[D].中国科学技术大学:2007.

[5] 贾攀,卢灿华,郝兆印. 叶蜡石的密封性能[J].工业金刚石, 2010,(6):99-104.

[6] 中南工业大学. 晶体X射线衍射学基础[M].北京:冶金工业出版社, 1990.216-217.

[7] 金柯，吴强，李欣竹,等.金和铂的室温等温物态方程及其压标的意义[J].高压物理学报, 2009,23(3):181-188.

[8] 汤文辉. 物态方程理论及计算概论[M].长沙:国防科技大学出版社,1999:184.

[9] Anjani K. Pandey, Brijesh K. Pandey, C. K. Singh2,ect. Analysis of isothermal EOS for NaCl under extreme compression[J]. Crystal Research Tech,2012, 44: 7420-7430.

[10] 谢刚,邱竹贤.熔融NaCl结构和热力学性质的分子动力学模拟[J].东北工学院学报,1991, 12(2): 130-134.

[11] 陈启武,熊湘君,邓福铭. 超高压技术研究[J].矿冶工程,2001, 21(1):62-65.

[12] 李立惟,盘瑛,冯吉福，等.金刚石复合片刀具磨损机理研究[J].超硬材料工程, 2010,25(5):8-11.

Equation of State of the Raw Materials for Super-hardComposite Synthesis and Its Application

FENG Ji-fu1,2,3, LIN Feng1,2,3, LI Li-wei3, HE Xu-Lin3

(1.GuangxiKeyLaboratoryofSupperhardMaterial,Guilin,China541004;2.NationalSpecialMineralMaterialsEngineeringResearchCenter,Guilin,China541004;3.ChinaNonferrousMetal(Guilin)GeologyandMiningCo.Ltd.,Guilin,China541004)

Based on the first-principles method of CASTEP, the relationship between pressure and the cell parameters of the common assembly materials for the high pressure cavity of cubic press within 30GPa has been studied, and the Bridgman equation of state of the common materials within the superhard material engineering pressure range (3～10GPa) has been provided. The Bridgman equation of state has been fitted based on the pressure-volume measured data of sodium chloride at 0℃～1800℃ under high pressure. And the effectiveness of the equation of state under the conditions of diamond compact synthesis has been discussed. The volume and structure of the assembly materials has been designed based on the the Bridgman equation of state of the materials and the compression ratio of the assembly materials within the high pressure cavity. The pressure inside the high pressure cavity has been significantly increased under the same gage pressure. The reliability of the design has been verified through experiment of diamond/ cemented carbide composite synthesis by cubic apparatus.

Computational Materials Science; equation of state; high-pressure cavity; assembly

2016-12-23

冯吉福(1973-)，男，教授级高工，主要从事超硬材料制备、有色金属冶金与综合利用方向研究。

冯吉福，林 峰 ，李立惟 ，等.合成超硬复合体原料的状态方程及应用[J].超硬材料工程，2017，29(2)：16-21.

TB332;TQ164

A

1673-1433(2017)02-0016-06