一次基于实测资料的海上搜救漂浮物的风漂系数优化实验
徐强强,肖文军,管琴乐,陆伟先
一次基于实测资料的海上搜救漂浮物的风漂系数优化实验
徐强强1,肖文军1,管琴乐1,陆伟先2
(1.国家海洋局东海预报中心,上海201200;2.国家海洋局宁波海洋环境监测中心站,浙江宁波315012)
基于2015年国家海洋局东海预报中心宁波中心站在舟山附近海域开展的一次模拟无动力船只和落水人员的海上漂移实验的实测资料,近似认为风致漂移速度与风速为线性关系,利用最优化算法计算了漂移轨迹预报中的最优风致漂移参数。计算结果表明:无动力船只的最优风致漂移参数分别为0.046 590 162,0.004 537 790,人的最优风致漂移参数分别为0.044 606 739,-0.003 190 774。当参数为最优时,预报漂移轨迹最接近实测;当参数接近最优值时,预报误差增长相对缓慢,在远离最优值时,预报误差增长相对快速。
拉格朗日追踪;优化算法;目标函数;舟山海域;风致漂移
1 引言
海上搜救目标常见有落水人员、船只等,搜救目标的漂移受到多方面因素的影响,其中主要有风和海流。物体的漂移速度可近似由流致漂移速度与风致漂移速度线性叠加获得。一般认为流致漂移速度等于流速,根据Breivik等的研究结果[1],风致漂移速度则与风速呈线性关系。风致漂移参数的选取对物体漂移轨迹预测至关重要。为了获得准确的风致漂移参数,国内外已在不同海域内对不同类型的船只和落水人员开展了模拟试验,例如加拿大2004年在纽芬兰东北进行的19组不同型号的救生筏和皮筏艇海上漂移试验[2],中国国家海洋局南海海洋工程勘察中心2011年在广东海域开展的3组模拟人和2组模拟无动力船只的漂移试验[3],以及此次国家海洋局东海预报中心宁波中心站2015年在东海水域开展的模拟无动力船只和人各一次的漂移试验等。
本文基于2015年国家海洋局东海分局开展的模拟无动力船只和人员的漂移试验所获得的逐时流速、风速和目标所在经纬度数据,构造能够衡量总体预报误差的目标函数,利用最优化算法获得能使预报误差最小的风致漂移参数——最优参数,为将来同海域内的无动力船只和人员搜救预报提供参考依据。
2 数据
本文的数据来源于2015年国家海洋局东海预报中心宁波中心站在舟山附件海域开展的无动力船只和假人漂移试验。试验在指定海域(30.49°N,122.87°E)投放船只模型和假人模型,对两者进行12 h的跟踪观测,跟踪期间每0.5 h观测一次海面风速风向、表层流速流向和物体漂移位置的经纬度。
搜救目标设置情况如下:
1)假人模型,材质为热塑混合胶,重约25 kg,宽40 cm,高150 cm,穿着救生衣,入水后处于水平状态;
2)无动力船只,重约45 kg,长225 cm,宽225 cm,高125 cm。考虑无动力船只模拟核定载重15人,因此以沙袋配重300 kg。无动力船只有蓬、有航标灯。

表1 漂移物基本参数
3 计算方法和设置
3.1 计算方法
如上所述,流致漂移速度等于流速,即:

式中:vcd表示流致漂移速度,vc表示流速。
将风速vw在东、北方向分解,得到uw、vw。风致漂移速度则与风速呈线性关系[1],则风致漂移速度vwd的东、北分量uwd、vwd可以表示为:

式中:a线性关系中的斜率,b为截距。将式(2)、式(3)写作向量形式,即:
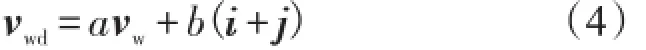
式中:vwd表示风致漂移速度,vw表示风速,a、b表示风致漂移参数,i、j分别表示东向和北向的单位向量。
物体漂移速度近似等于流致漂移速度与风致漂移速度之和,结合式(1)、(4),物体的实际漂移速度可以表示为:

式中:vd表示物体漂移速度。
根据肖文军等[4]拉格朗日追踪中,漂移位移与漂移速度的关系可以表示为:


式中:dt表示时间间隔,dx、dy表示一个时间间隔内的位移,u0、v0表示一个时间间隔内的初始漂移速度东、北分量,du、dv表示一个时间间隔内的漂移速度东北分量的增量。
3.2 计算设置
以不同时刻模拟的物体漂移位置与实际观测位置的距离的平方和作为衡量预报结果好坏的目标函数:

式中:J表示目标函数,i表示不同预报时刻,px、py表示预报的物体位置,ox、oy表示观测的物体实际所处位置。从目标函数定义来看,J越大表示预报准确度越差,越小准确度越好。不难看出a、b的改变会导致J改变,因此J为a、b的函数,即:

参数约束范围:管琴乐等[5]曾将多组参数输入漂移预测模型,经过比对发现比较合理的漂移参数为:a=0.04,b=0。参考管琴乐等的前期工作,将参数约设为0.02≤a≤0.06,-0.02≤b≤0.02。
定义以下最优化问题:
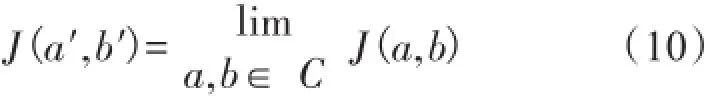
式中:C表示参数a、b的约束范围。由式(10)可知,最优参数a′、b′即是能令目标函数J取到最小值的解。
优化算法:利用谱投影梯度(Spectral Projected Grad,SPG)优化算法[6]对式(10)进行求解。SPG优化算法流程图如下。

图1 SPG优化算法流程图
4 结果与分析
参数优化的结果显示,对于假人漂移,最优风致漂移参数为:a=0.044 606 739,b=-0.003 190 774;而对于船只,最优风致漂移参数为:a=0.046590162,b= 0.004 537 790。为了对最优风致漂移参数进行验证,我们将最优参数与管琴乐等[5]的参数设置分别输入漂移轨迹预测模型,对结果进行比较。数值实验表明,如果选用最优参数,假人和船只案例的目标函数分别为7.815323457e+6和1.013838095e+7m2;而如果采用a=0.04,b=0的参数设置,则假人和船只案例的目标函数分别为1.495 758 496e+7和9.555 511 876e+7 m2。可以看出采用最优参数的目标函数值要小很多,这说明最优参数对于假人和船只漂移预报准确性总体上都有改善;而且最优参数令船只案例的目标函数减小的幅度很大,这说明其对船只案例的改善尤为明显。
为了直观地比较不同参数设置下的漂移过程,我们做出了不同参数设置下的预报路径和实际漂移路径图.总体来说(见图2),最优参数下的预报路径要更加靠近实际路径。最优参数设置相比管琴乐等[5]的参数设置对于前期路径预报没有很显著的改善;但对后期的路径预报则有较为显著的改善。另外值得一提的是,文章为了尽可能展现最优参数的优势,而保留了多位有效数字,但在实际的业务应用中一般是将参数有效位数保留1~2位。

图2 预报路径和实际路径(黑色为实际路径,黄色为参数a=0.04、b=0,红色为最优参数)。

图3 目标函数等值线图
我们以参数a为横坐标,b为纵坐标,做出图3目标函数的等值线图。图3中,目标函数的最小值点所处坐标正对最优参数,这也符合之前的计算预期,即最优参数能使目标函数最小。从图3可以看出,目标函数在横向上变化迅速(等值线密集,几乎与横向垂直),而在纵向变化缓慢(等值线稀疏,几乎与纵向平行),说明目标函数对参数a十分敏感,对参数b则相对不敏感。目标函数在靠近最优参数点附近的区域内等值线稀疏,越远离该区域等值线越密集,说明目标函数在离最优参数点越远的区域对参数越敏感。总的来说,预报准确性受参数a的影响要远高于b;且在靠近最优参数的区域内受参数变动影响要小于远离最优点区域。
5 讨论

式中:m为漂移实验次数,α为权重系数。对式(11)的目标函数进行优化便可以得到多次实验下的最优参数,此最优参数将更具可靠性。
本文采用的参数优化方法可以将同区域内多
本文基于假人和船只海上漂移实验的数据,对追踪模型参数进行了最优化。优化结果显示最优参数可以改善物体漂移预报准确性。从目标函数在参数相空间上的结构来看,参数a对预报准确性的影响要远大于参数b。目标函数在最优参数点附近有个“稳定区”,若参数位于“稳定区”内,那么参数误差对目标函数的影响相对较小,因此预报工作应尽可能将参数设置在最优点附近的“稳定区”内。
另外,本文只是基于假人和船只各一次的实验进行了参数最优化,因此并不足以作为最终的最优参数。不过,如果能获取多次漂流实验的实测数据,可以将目标函数重新定义为:次同类型实验的结果进行合理的统合,处理大量的实验数据时十分方便,未来随着实验数据的累积,此项优势将愈发明显。另外在实际操作中,海上搜救漂浮物的实际漂移速度不易观测。本方法可以避免观测漂浮物漂移速度,只需观测风速、流速和漂浮物的坐标位置3个要素,而这三者都属于常规观测要素,操作简便。本文方法对于未来同类型参数优化工作(尤其是在缺少漂浮物漂移速度数据的情况下)可作为参考。不过,本文方法也有局限性,最主要的就是需要多次重复实验支撑,重复实验的漂浮物规格也必须相近;如本文所做,基于一次观测实验优化的参数只可以作为参考,不足以作为最终用于业务预报的参数。
[1]Breivik Ø,Allen AA.An Operational Search and Rescue Model for the Norwegian Sea and the North Sea[J].Journal of Marine Systems,2008,69(1-2):99-113.
[2]Choisnard J,Power D,Randell C,et al.Toward the Use of Earth Observation Wind Data for Marine Search and Rescue Operations [C]//Proceedingsof2006IEEEInternationalConferenceon Geoscience and Remote Sensing Symposium.Denver,CO,USA: IEEE,2006:4084-4087.
[3]周水华,杨阳,冯伟忠.广东海域模拟人和无动力渔船海上漂移试验研究[J].热带海洋学报,2013,32(1):87-94.
[4]肖文军,堵盘军,龚茂珣,等.上海沿海海上搜救预测模型系统的研究和应用[J].海洋预报,2013,30(4):79-86.
[5]管琴乐,肖文军,李旋,等.基于海上试验的搜救预测模型探讨[C]//2015年度东海区海洋科学技术与应用学术交流会.2015: 21-31.
[6]Birgin E G,Martínez J M,Raydan M.Nonmonotone Spectral Projected Gradient Methods on Convex Sets[J].SIAM Journal on Optimization,2000,10(4):1196-1211.
A parameter optimizing experiment of wind-induced velocity of rescuing floating object in the sea based on an observing project
Xu Qiang-qiang1,XIAO Wen-jun1,GUAN Qin-le1,LU Wei-xian2
(1.Forecast Center for East China Sea,SOA,Shanghai 201200 China;2.Ningbo marine environment monitoring center,SOA,Ningbo 315012 China)
Based on the data observed from drifting experiments including ship without motor and people in the seawater conducted by the Ningbo center station of forecast center for East China Sea SOA in 2015,assuming the linear relation between the wind-induced velocity and wind velocity,using the optimal algorithm,the optimal parameters of wind-induced velocity are calculated.The results show that the optimal parameters of windinduced velocity for the ship without motor are 0.046 590 162,0.004 537 790,and for the people in the seawater are 0.044 606 739,-0.003 190 774.When the parameters are optimal,the predicting drifting trajectories are most close to the observed drifting trajectory.The predicting errors grow slowly when the parameters are close to the optimal values,while grow fast when the parameters are far from the optimal values.
Lagrange tracing;optimizing algorithms;object function;Zhoushan sea area;wind-induced drift
U676.8+3
A
1003-0239(2017)02-0067-05
10.11737/j.issn.1003-0239.2017.02.009
2016-06-27;
2016-08-12。
国家海洋局海洋公益性行业科研专项(201405022-3)。
徐强强(1987-),男,助理工程师,硕士,从事数值模拟及可预报性研究。E-mail:xu28735@163.com

