大豆期货与豆油期货的价格关系
——基于大连商品交易所的经验分析
刘立军,赵立三
(1.河北农业大学 商学院,河北 保定 071001;2.河北地质大学 经贸学院,河北 石家庄 050031;3.河北大学 管理学院,河北 保定 071002)
大豆期货与豆油期货的价格关系
——基于大连商品交易所的经验分析
刘立军1,2,赵立三3
(1.河北农业大学 商学院,河北 保定 071001;2.河北地质大学 经贸学院,河北 石家庄 050031;3.河北大学 管理学院,河北 保定 071002)
大豆是大豆油的原材料,大豆的期货价格变动是否顺向影响了豆油的期货价格?豆油的期货价格变动是否反向影响了大豆的期货价格?运用大连商品交易所2006年1月9日至2016年8月4日10年的经验数据,使用黄大豆1号收盘价和豆油的收盘价构建VAR模型进行实证分析,并通过Granger因果关系检验、方差分解分析和脉冲响应函数表明:大豆期货价格的变动对豆油期货价格的变动具有明显地顺向影响和贡献度,豆油期货价格变动对大豆期货价格变动的反向影响不明显。
大豆期货价格;豆油期货价格;VAR
一、 引 言
商品期货交易活动是指买卖双方共同约定在未来的某一时间、按照约定价格进行交割的一种贸易活动。从过去的口头承诺到 “标准化期货合约”,这种远期合同交易合约提供了指导未来生产经营活动的价格信号,对冲农业生产中的不确定性和长期贸易的风险,从而起到了防范价格波动造成市场风险的作用,使得农业生产经营活动更为有序进行。那么,大豆在期货市场上的价格是否影响了大豆油的期货价格呢?大豆是大豆油的原材料,大豆期货价格变动是否顺向影响了豆油的期货价格?豆油的期货价格变动是否反向影响了大豆的期货价格?本文运用大连商品交易所2006年1月9日至2016年8月4日10年的经验数据,分析大豆期货价格与豆油期货价格的传导关系,以期发现我国大豆期货价格和豆油期货价格的形成机制以及变化规律,为大豆农业生产、大豆期货、豆油期货投资提供决策参考。
在以往的研究中,从交易和监管等角度对期货进行了多方探讨。认为期货是一种未来交易,买卖期货合约为买家和卖家提供了一个可以在未来日期交付的合同,从而实现预测未来农产品交易价格的走势[1]。期货为投资者和农产品的贸易之间建立了联系,从而使得私人的投机资本一直活跃于农产品贸易中。买卖期货合约是一种投机交易,是基于对不确定性的价格走势的预测所获得回报,因而,期货交易更像是一场赌博,这也使得期货交易一直备受争议。支持者们认为,期货通过商品交易所可以为农业的商业化集中组织和管理提供价格信息和风险控制等服务[2-3]。而一些农民和农民组织则对期货交易持不信任态度,因为期货交易的存在,使得一些非农利益集团利用期货交易来操纵价格和市场。尽管各国在期货交易发展的历史上都对金融投机行为制定了各种限制措施,还是无法改变期货交易的不断增长和投资者对期货的青睐[4]。19世纪后期,在美国的小麦期货市场中,期货合约的虚拟交易额已经超过了大宗商品的现货交易[5]。
在现代经济中,期货市场的存在已经是农业生产的重要组成部分,期货所具有的价格发现功能可以大大降低农产品价格波动的风险。期货的价格发现功能是期货的一个重要功能,国外很多学者也对此展开了研究。Kumar Mahalik等采用向量误差修正模型和二元指数Garch模型分析印度现货、期货商品市场价格发现和波动溢出效应[6]。Cornell研究了成交量的变化量户商品的期货价格和现货价格之间的关系[7]。Bhanumurthy通过分析印度气候的剧烈变化对现货和期货价格形成的影响后认为,价格发现机制的薄弱会最终导致更高的价格波动[8]。Mishra对天然气的期货价格和现货价格进行研究后,发现天然气的期货价格不能预测未来天然气的现货价格[9]。
国内很多学者也对此展开了研究。黄飞雪等利用协整检验的方法研究了金融危机对我国大连商品交易所的大豆和豆粕期货价格之间的关系,认为我国应大力加强农产品期货市场,解决“三农”问题[10]。何诚颖等利用VEC模型和脉冲反应函数对沪深300指数期货和现货的1分钟高频数据分析后认为,沪深300指数期货对价格的发现能力要超过现货价格[11]。赵华等构建ARMAJI-GARCH模型描述了我国金属期货价格的跳跃性行为的价格发现作用[12]。方匡南等利用沪深300股指期货5分钟高频数据,引入分位数回归,分析了不同涨跌幅度的期货价格和现货价格的关系[13]。
在研究期货价格的发现机制时,学者们大多立足于研究期货价格与现货价格之间的关系,鲜有研究商品的期货价格同其上下游行业的商品期货价格的关系。本文选取大豆的期货价格和其下游行业的豆油期货价格进行实证分析,尝试描述它们之间的相关关系。
二、向量自回归(VAR)模型及估计方法
向量自回归模型是一种非结构化的模型,模型通过对现实中的经济数据来确定整个经济系统的动态关系,而不是依靠经济理论。因此在建立VAR模型时不用事先提出理论上的假设,而是通过对现代的经济时间序列所提供的信息来验证各经济变量之间的理论关系。
VAR模型的表达式:
Yt=μ+A1Yt-1+…+ApYt-p+ε1
t=1,2,…,T
其中,
μ=(μ1,μ2,…μk)′;ε=(ε1t,ε2t,…,εkt)′
这是一个含有k个变量的VAR模型,Yt表示k维内生变量向量,p为滞后阶数,T为样本数,A1,…,Ap为k×k维的系数矩阵,ε是k维扰动向量。
三、 变量选择及统计性描述
(一)数据选取
本文所取的数据为大连商品交易所2006年1月9日至2016年8月4日的黄大豆1号和豆油的收盘价的每日数据,共2 005个样本,数据均来自wind资讯。由于期货合约大多是有交割期的,一般都不超过一年,本文为研究方便,数据选取了“连续合约”的数据。在大连商品交易所的期货交易中有黄大豆1号和黄大豆2号两个品种,黄大豆2号的成交量远远低于黄大豆1号的成交量,因此本文选取黄大豆1号代表黄大豆期货的价格走势。本文的所有数据处理均利用软件Eviews8.0。
(二)数据统计说明
通过对两个变量的描述性统计分析(表1),以及黄大豆1号和豆油期货价格走势(图1)可以看出,两个变量的价格趋势具有一定的一致性,价格波动的周期基本一致。豆油作为大豆的下游产品,大豆期货价格的变动与豆油期货的价格变动是具有相关性的,对其进行协整检验,大豆期货价格变动与豆油期货价格存在协整关系,这表明作为大豆的下游行业的豆油期货价格与大豆期货的价格具有长期的均衡关系。

表1 变量的描述性统计分析
注:J-B 表示 Jarque -Bera检验
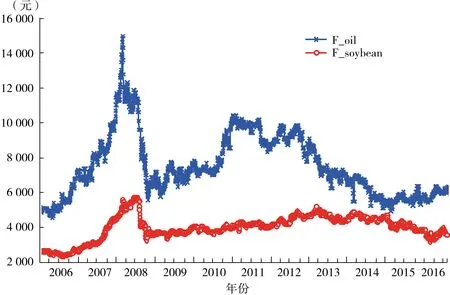
图1 黄大豆1号和豆油期货价格走势
四、 实证研究
本文建立VAR模型对大豆和豆油的期货价格的相关关系进行实证分析。首先运用单位根检验判断两个变量的平稳性,然后确定滞后阶数,建立VAR模型。再对模型的稳定性进行检验后依次进行Granger因果检验,方差分解分析和脉冲响应函数分析。
(一)ADF检验
为了避免所建立的模型出现伪回归问题,建立VAR模型要求所有变量同阶单整。因此,在建立VAR模型之前,首先要求对各变量进行单位根检验,本文采用ADF检验对各变量的平稳性进行检验,检验结果如表2所示。由检验结果可以看出,黄大豆1号(F_soybean)和豆油(F_oil)在1%的显著水平下都是一阶单整I(1)序列,进一步进行协整检验,检验表明两变量协整,说明存在长期稳定均衡关系。
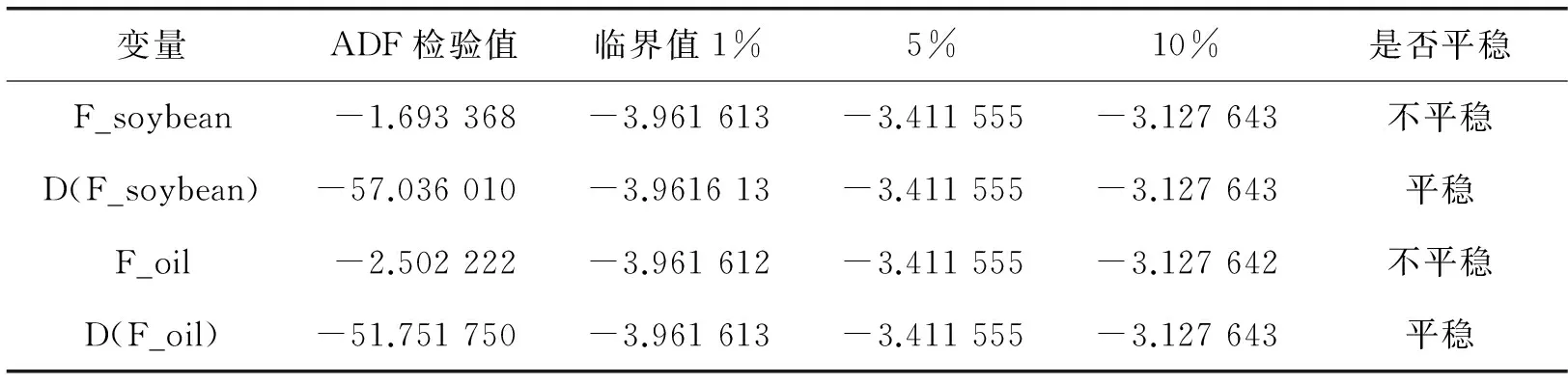
表2 变量的ADF检验结果
(二)构建VAR模型
由上述分析可知,变量F_soybean和F_oil为I(1)序列,如果直接建立VAR模型,会造成模型不稳定而且脉冲响应函数不收敛,致使脉冲响应函数没有意义,为此,本文采用两个变量的一阶差分建立VAR模型。
1.滞后阶数的确定。构建VAR模型时,需要确定滞后阶数,如果滞后阶数过多,会造成需要估计的参数过多,影响模型的自由度;如果滞后阶数过少,则会无法反应模型的整体特征[14]。本文综合考虑LR统计量、FPE最终预测误差、 AIC信息准则、SC信息准则、HQ信息准则,运用Eviews8.0考察滞后阶数,结果如表3所示。在各种检验的结果中,FPE最终预测误差、 AIC信息准则、SC信息准则、HQ信息准则4个指标的检验结果为滞后2期是最佳滞后期,LR统计量检验结果为滞后7期是最佳滞后期,根据多数准则,确定滞后阶数为2,并建立滞后阶数为2期的VAR(2)模型。
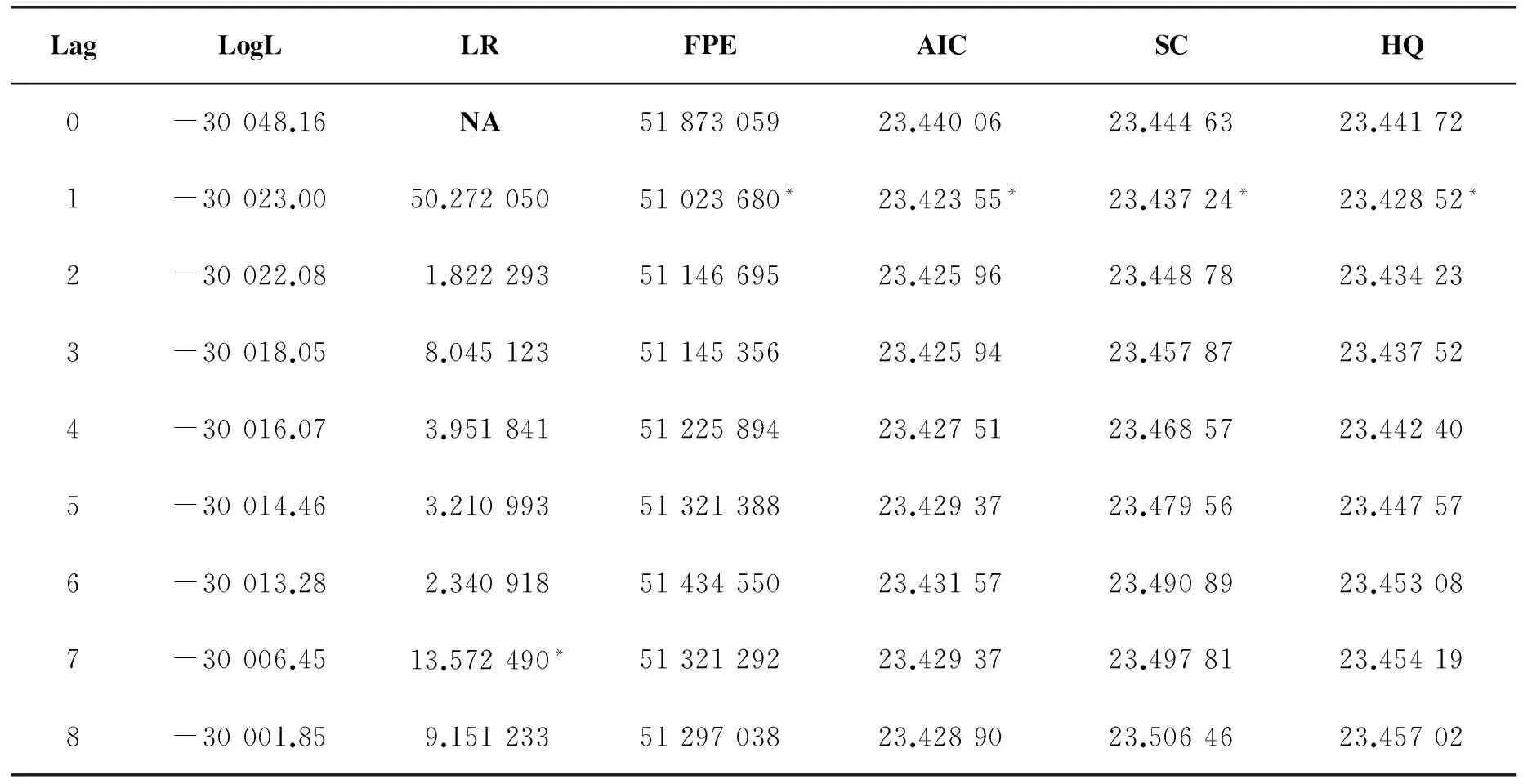
表3 滞后阶数的确定
*indicates lag order selected by the criterion. LR: sequential modified LR test statistic (each test at 5% level)
FPE: Final prediction error.AIC: Akaike information criterion.SC: Schwarz information criterion.
2.模型的稳定性检验。为了确保脉冲响应函数的收敛性,构建VAR模型后,首先要对模型的稳定性进行检验。检验结果如表4和图2所示。表明本文所构建的VAR模型的根的模均小于、而且处于单位圆内,说明本文所构建的VAR模型是稳定的。
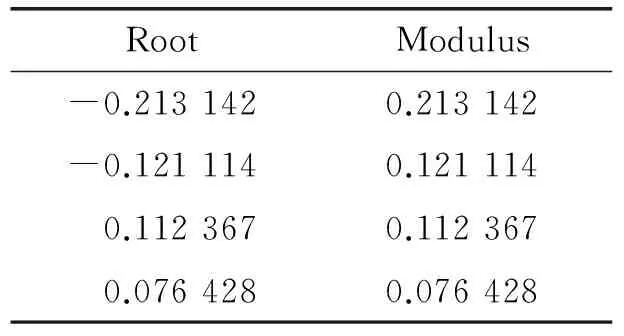
表4 AR Roots Table
No root lies outside the unit circle.
VAR satisfies the stability condition.
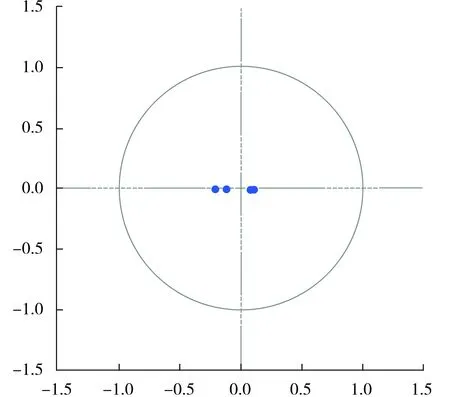
图2 Inverse Roots of AR Characteristic Polynomial
3.Granger因果关系检验。利用VAR模型可以检验经济时间序列的各变量之间的因果关系。为了探讨当黄豆期货价格变动是否能够引起豆油的期货价格变动,豆油期货价格的变动能否引起黄豆期货价格的变动,本文采用Granger因果关系对此进行检验,结果如表5所示。
在D(F_oil)方程中,拒绝D(F_soybean)不是D(F_oil)的Granger原因的原假设,表明大豆期货价格对豆油期货价格具有显著的Granger影响,大豆期货价格是豆油期货价格的Granger原因。
在D(F_soybean)方程中,不能拒绝D(F_oil)不是D(F_soybean)的Granger原因的原假设,表明豆油期货价格对大豆期货价格不具有显著的Granger影响,豆油期货价格不是大豆期货价格的Granger原因。

表5 Granger 因果关系检验
Dependent variable: D(F_oil),Dependent variable: D(F_soybean)
(三)方差分解分析
对VAR进行方差分解分析,可以观察各变量的贡献程度,用来分析在每个结构冲击中,对内生变量变化的贡献度。
表6为D(F_soybean)和D(F_oil)的变化量对D(F_soybean)变化量的贡献程度,结果显示,豆油期货价格变化量对大豆期货价格变化量的贡献度从滞后2期到滞后6期逐渐增加,到滞后期达到0.001 835%,并保持稳定。总的来说,豆油期货价格变化量对大豆期货价格变化量的贡献率很低,说明豆油期货价格变化量对大豆期货价格变化量几乎没有影响,这与上述的豆油期货价格不是大豆期货价格的Granger原因的分析相吻合。
表7为D(F_soybean)和D(F_oil)的变化量对D(F_oil)变化量的贡献程度,结果显示,大豆期货价格变化量对豆油期货价格变化量的贡献度从滞后1期到滞后4期逐渐增加,于滞后4期达到峰值4.432 809%,并保持稳定。由此可以看出,大豆期货价格的变化量对豆油期货价格的变化量具有明显的贡献率,这同时也与上述大豆期货价格是豆油期货价格的Granger原因的分析结果相吻合。
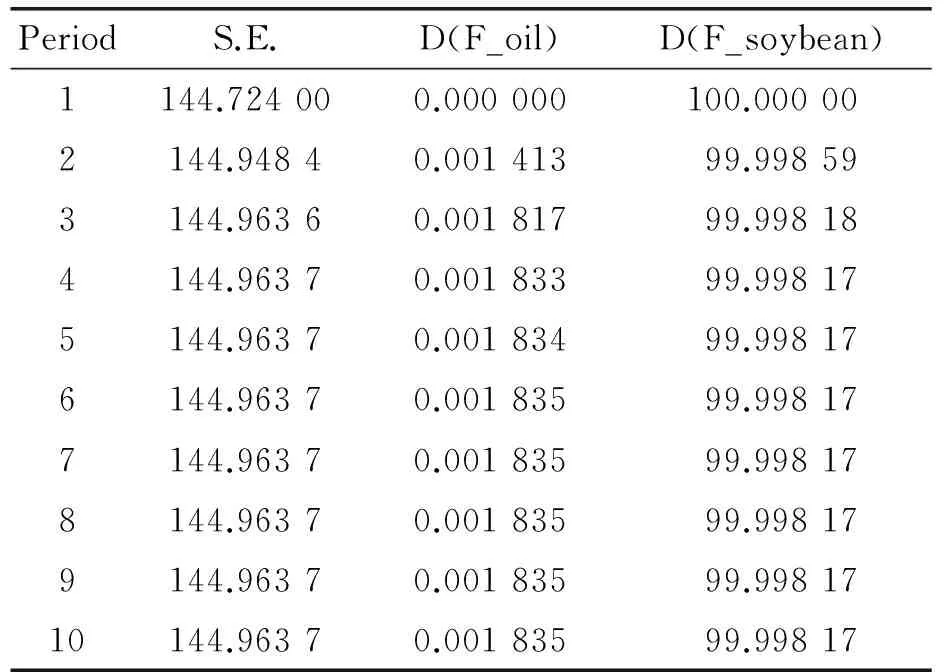
表6 Variance Decomposition of D(F_soybean)
Cholesky ordering: D(F_soybean) D(F_oil)
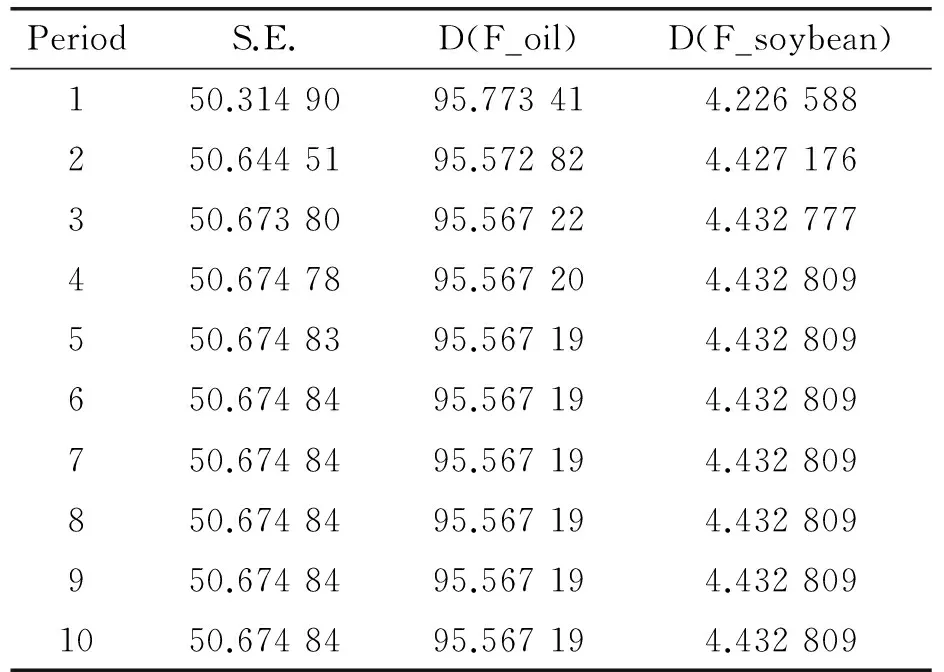
表7 Variance Decomposition of D(F_oil)
Cholesky ordering: D(F_oil), D(F_soybean)
(四)脉冲响应函数
脉冲响应函数所描述的是在其中一个内生变量的随机误差项上施加一个标准差大小的冲击后,对所有的内生变量的当期值和未来值的影响,只有在每个向量都平稳、模型也平稳的状态下,脉冲响应函数才是收敛的,本文满足脉冲响应函数的条件,结果如图3和图4所示。
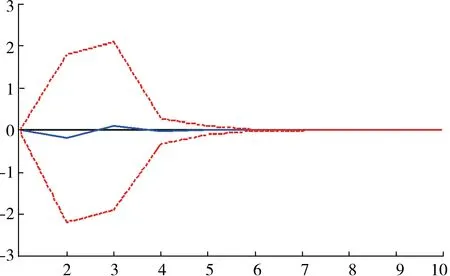
图3 Response of D(F_soybean) to Cholesky One S.D. D(F_oil) Innovation
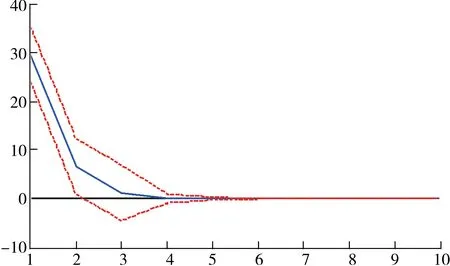
图4 Response of D(F_oil) to Cholesky One S.D. D (F_soybean) Innovation
图3所示,当在本期给豆油期货价格一个正冲击之后,大豆期货价格在前4期上下小幅度震荡,并于第3期达到峰值,此时峰值为0.102 041,即在3期,D(F_soybean)对D(F_oil)的响应是0.102 041,从第4期开始趋于平稳。这表明,当豆油期货价格受到外部条件的某一冲击后,会传递给大豆期货,给大豆期货价格造成同样的冲击,但是这一冲击的作用很微弱,并不显著。
图4所示,当在本期给大豆期货价格一个正的冲击后,豆油期货价格在第1期即达到峰值29.753 32,即在第1期,D(F_oil)对D(F_soybean)的响应是0.102 041。从第1期开始,逐渐下降,到第6期后趋于平稳。这表明当大豆期货价格受到外部条件的某一冲击后,会传递给豆油期货,而且这一冲击具有显著的作用。
五、结 论
本文通过对大连商品交易所2006年1月9日至2016年8月4日的黄大豆1号和豆油的收盘价的每日数据进行ADF检验,序列都是一阶单整的,符合构建VAR模型的条件。并且对所构建的VAR模型进行平稳性检验后显示,模型平稳。
通过Granger因果关系检验,表明大豆期货价格对豆油期货价格具有显著的Granger影响,大豆期货价格是豆油期货价格的Granger原因;豆油期货价格对大豆期货价格不具有显著的Granger影响,豆油期货价格不是大豆期货价格的Granger原因。通过方差分解分析可知,豆油期货价格变化量对大豆期货价格变化量的贡献率很低,豆油期货价格变化量对大豆期货价格变化量几乎没有影响;大豆期货价格的变化量对豆油期货价格的变化量具有明显的贡献率,这同时也与上述大豆期货价格是豆油期货价格的Granger原因的分析结果相吻合。最后,由脉冲反应函数可以看出,当豆油期货价格受到某一外部条件的冲击后,会传递给大豆期货,给大豆期货价格造成同样的冲击,但是这一冲击的作用很微弱,并不显著。当大豆期货价格受到某一外部条件的冲击后,会传递给豆油期货,而且这一冲击具有显著的作用。
结论表明,大豆作为豆油生产的原材料,大豆期货价格的变动明显地顺向影响了豆油期货价格的变动,而豆油期货价格的变动反过来对大豆期货价格变动的影响并不显著。
[1]CRONON W. Nature’s Metropolis: Chicago and the Great West[M]. New York: W.W. Norton, 1992:120-121.
[2]IRWIN S H, D R SANDERS. Financialization and Structural Change in Commodity Futures Markets[J]. Journal of Agricultural and Applied Economics, 2012,44 (3): 371-396.
[3]HIERONYMUS T A. Economics of Futures Trading, for Commercial and Personal Profit[M]. Chicago: Commodity Research Bureau,1977:9-11.
[4]COWING C B. Market Speculation in the Muckraker Era:The Popular Reaction[J]. The Business History Review, 1957, 31(4): 403-413.
[5]Worthy M.Broken Markets: How Financial Market Regulation Can Help Prevent Another Global Food Crisis[M/OL]. London: World Development Movement,2011[2015-05-20].http://www.globaljustice.org.uk/sites/default/files/files/resources/ broken-markets.pdf.
[6]KUMAR MAHALIK MANTU, ACHARYA DEBASHIS,SURESH BABU M. Price Discovery and Volatility Spillovers in Futures and Spot Commodity Markets: Some Indian Evidence[J]. Journal of Advances in Management Research,2014,11(2): 226-211.
[7]CORNELL BRADFORD. The Relationship Between Volume and Price Variability in Futures Markets[J].The Journal of Futures Markets,2000,20(1): 5-18.
[8]BHANUMURTHY N R, DUA P,KUMAWAT L. Weather Shocks, Spot and Futures Agricultural Commodity Prices-An Analysis for India[Z/OL].Working Paper, 2012[2012-02-19].http://cdedse.org/pdf/work 219.pdf.
[9]MISHRA VINOD,SMYTH RUSSELL. Are Natural Gas Spot and Futures Prices Predictable? [J].Economic Modelling,2016 (54): 178.
[10]黄飞雪,王治华. 基于协整的金融危机前后DCE大豆与豆粕期货价格关系的比较[J]. 农业技术经济,2010(6):44-53.
[11]何诚颖,张龙斌,陈薇. 基于高频数据的沪深300指数期货价格发现能力研究[J]. 数量经济技术经济研究,2011(5):139-151.
[12]赵华,王一鸣. 中国期货价格的时变跳跃性及对现货价格影响的研究[J]. 金融研究,2011(1):195-206.
[13]方匡南,蔡振忠. 我国股指期货价格发现功能研究[J]. 统计研究,2012(5):73-78.
[14]李子奈,叶阿忠.高级应用计量经济学[M].北京:清华大学出版社,2012:103-104.
【责任编辑 郭 玲】
Study on the Relationship Between Soybean Futures and Soybean Oil Futures Prices——Basing on the Empirical Analysis of Dalian Commodity
LIU Li-jun1,2, ZHAO Li-san3
(1. School of Business, Agricultural University of Hebei, Baoding, Hebei 071001;2. School of Economics and Trade, Hebei University of Geology, Shijiazhuang, Hebei 050031;3. College of Management, Hebei University, Baoding, Hebei 071002, China)
Soybean is the raw material of soybean oil. Does the change of soybean futures prices affect the change of soybean oil futures prices or vise versa? In this paper, a case study is given to analyze the construction of VAR model with the closing price of yellow bean No.1 and soybean oil in Dalian Commodity Exchange from Jan. 9th, 2006 to Aug. 4th, 2016. Through Granger causality test, variance decomposition analysis and impulse response functions, it indicates that the effects of the change of soybean oil futures prices on the change of soybean futures price are not obvious, while the change of soybean futures prices has obvious influences and high contribution on the change of soybean oil futures prices.
soybean futures prices; soybean oil futures prices; VAR
2016-09-12
国家社科基金重点项目(15AZD006);河北省教育厅人文社会科学重大课题攻关项目(ZD201421);河北省社会科学基金项目(HB14YJ036、HB15YJ052、HB15YJ056)
刘立军(1980—),女,河北承德人,河北农业大学商学院博士研究生,河北地质大学经贸学院讲师,主要研究方向:农业经济管理。
F830.9
A
1005-6378(2017)02-0103-07
10.3969/j.issn.1005-6378.2017.02.015

