PWM逆变器采样通路传导噪声的分析与抑制
刘西强


摘 要
提高开关管的开关频率,可以提高输出电压的电能质量,增强PWM变换器的动态调节性能。然而,较高开关频率的应用使得开关过程引起的高频噪声对控制系统的采样产生更加深刻的影响。本文主要针对PWM逆变器传导噪声产生源和采样调理电路的传导通路进行分析,并利用实验测得噪声传导等效电路中各无源器件的参数。通过对该等效电路进行时域分析,采用一种简单的传导噪声抑制方法。仿真结果与实验结果基本一致,证明了共模传导等效电路模型及其分析的正确性。
【关键词】PWM逆变器 采样 共模传导 抑制
1 引言
PWM调制策略广泛应用于需求高效的电能转换效率与较低的波形畸变率的场合,且在中低功率等级的变换器中的应用尤为突出。随着新型器件的发展,新型MOSFET与IGBT的开关频率日渐增加。由开关器件引起的电磁干扰问题严重影响控制系统的穩定性。当前PWM逆变器的开关频率通常为几十到几百kHz,其引起的电磁干扰噪声中传导噪声频谱较为丰富。EMI滤波器通常设置为抑制开关频率处的开关噪声,并不能滤除所有频次的噪声。电磁干扰包括两项:共模干扰和差模干扰。差模干扰主要是由高频开关引入的差模脉动电流引起的。共模干扰主要是通过开关管在开关过程中对杂散电容的充放电引起的,且共模干扰是传导干扰的主要成分。
针对PWM逆变器的高频共模干扰的分析已进行了很多研究。现有文献中针对PWM逆变器与BUCK变换器的电磁干扰问题展开研究的占大多数,且其噪声传导通路主要集中于变换器与负荷间,而针对共模干扰对采样通路影响的研究较少。采样共模干扰通路中包含多种组件,且各单元在高频工况下的杂散参数较为复杂。研究中三相互感器的数值模型针对高压高频应用中开展,针对采样回路中的三相低压互感器高频模型分析可借鉴三相电力变压器和互感器的高频等效模型解决实际工程问题。
本文针对PWM逆变器的采样通路的传导噪声途径进行分析,并针对共模干扰源与主要传导单元的高频等效模型进行分析与验证。文中尝试采用了一种简单的共模干扰抑制方法,实验验证了该方法的有效性。
2 采样通路共模干扰路径分析
共模电流传导通路有两个方向,一个是前向传导:至逆变器的输入侧。另一个通路是后向传导:至逆变器输出侧。本文讨论的对采样通路的影响,即由后向传导产生。
2.1 共模干扰源
在高频dv/dt及杂散电容的辅助作用下,PWM逆变器产生的共模电压形成共模电流通路。各开关管与底层散热片间装有导热硅脂,使得开关管的集、射极与底层散热片之间构成一个较大的杂散电容。当前常用的PWM逆变器控制策略中,开关频率较高,开关管电压的突变迅速,可高达8.57GV/s。开关管频繁开断,并持续对杂散电容充放电,从而产生传导性共模电流。
以A相为例进行分析。对于阻感性负载,假定A相电流iA>0。由于采用的PWM开关频率较高(12kHz),在iA>0期间,A相上、下桥臂的IGBT会导通多次。若起始时刻VT1导通,则iA流向如图1(a)中的虚线所示。在VT1关断时刻控制系统给关断信号,经过微秒级的死区时间后VT4导通,由于负载电流不能突变,此时开关管VT4实际上尚未导通,A相电流即从VT1向VD4转移,如图1(b)所示,此时,VD2压降为零,Ud、VT1、VD2环路的KVL方程为:
L为环路的杂散电感,包括母排、IGBT内部寄生电感和引线电感等。
因此,A相桥臂的等效电路如图1(c)所示。Cp为开关管与散热器间的等效电容。与Cp相比,母线电容容值非常大,可忽略。Cn是电解电容之后的直流母线正负极对参考地的杂散电容。且A、B、C三个桥壁等效电路相同,将三个桥壁电路进行叠加,可得到如图1(d)所示干扰源模型。当iA<0时,A相桥臂的开关状态分析与iA>0时类似。
2.2 电压互感器模型
高频变压器T型等效模型中,引起传导噪声干扰的杂散参数主要是初次级绕组之间的杂散电容Cps,该电容的存在使得变压器初级向次级耦合能量的能力降低,此时次级绕组对初级绕组相当于一个高频阻抗负载。
在本文的分析中将三相电压互感器看作由三个独立的单相电压互感器构成,见图2。其分布电容等效为三类集总电容,其中包括初级绕组杂散电容Cp,次级绕组杂散电容Cs以及初级绕组与次级绕组之间的杂散电容Cps。其中Cp和Cs分别体现了初级和次级线圈储存的电场能量的能力,Cps表示的是初级次级电场耦合的能力,是影响传导电流大小的重要因素之一,也是分析共模噪声干扰时主要考虑的一个参数。Rp和Rs是初级次级绕组电阻,Lp和Ls分别代表初级次级漏感,T代表理想变压器。Cpg与Csg分别代表初级次级中性点对地的等效杂散电容。
该等效电路中分布电容与二端口网络中各电容有如下对应关系:
Cp=Cpo+(1-k')Cpso
Cs=k'2Cso+k'(k'-1)Cpso
Cps=k'Cpso
其中,Cxo,(x代表p、s、ps)代表折算前次级绕组的等效电路参数。
根据共模电流的传输路径的分布参数可知,共模电流在ABC三相中的大小相等且同向。将图2中ABC三相进行并联等效,结果如图3所示。其各电容参数可以通过阻抗频率分析仪进行测量。
2.3 采样与调理电路分析
电压采样电路的输入端Vap电压信号最大值为4.7V,对应线电压的峰值为580V。如图4所示,将两个输入电压信号做差后进行1.5V的直流偏置,然后经过滤波电路滤除高频谐波分量,最后经反相器送入DSP。调理电路的输出端VabAD为0~3V信号。在此已省略放大器的供电电源电路。
3 仿真和实验
本文采用Saber对三相PWM逆变器传导干扰模型进行了时域仿真和频域分析。实验中,直流母线电压为580V,无源器件的参数采用LCR电桥测量。在开关频率为12kHz条件下,逆变主电路杂散参数见表1,电压互感器的杂散参数见表2。
本文仿真对比了采样电路中的电压信号Vab在PWM控制器开关周期为12kHz与6kHz条件下的采样电压信号。
图5所示为开关频率变化时的Vab波形及其频率特性分析结果。在开关频率为6kHz时,采样效果较好,但仍存在较为明显的正弦“波带”,而开关频率增至12kHz时,采样效果变的更差,从频域分析结果可以看出,随着频率的增加,不仅开关频率处的谐波含量增加,高频段的高频谐波含量也显著增加。
实验参数设置:PWM逆变器的直流输入电压为580V,交流输出电压为380V,直流电容采用四个4700uF的电解电容进行串并联。开关器件选用英飞凌IGBT (BSM150GB12DN2),PWM控制采用SVM控制方式,开关频率12kHz。
测量Vab点电压如图所示。通道二为逆变开环控制的输出电压,其电压有效值基本为指令值。通道四即为采样调理电路的实测波形,采样电路中存在较大的采样噪声,在控制器闭环控制中实际输出电压有效值偏差较大。
从共模电压传导干扰的通路方面考虑,在高频工作条件下,较大的电压互感器的杂散电容使得逆变器产生的共模干扰噪声传递到采样电路。若在不改变实验台架的基础上,若能够在互感器与采样电路间增值电容器,为功率电路产生的传导噪声提供闭合回路,则能够有效抑制传导噪声对采样电路的干扰。
具体方法是在电压互感器后端增置三个10uF共模电容,见图3中的Cfx(x代表A,B,C)。仿真结果见图。从图7可以看出,增值共模滤波电容后,采样通路的采样“波带”的现象得到了有效抑制。
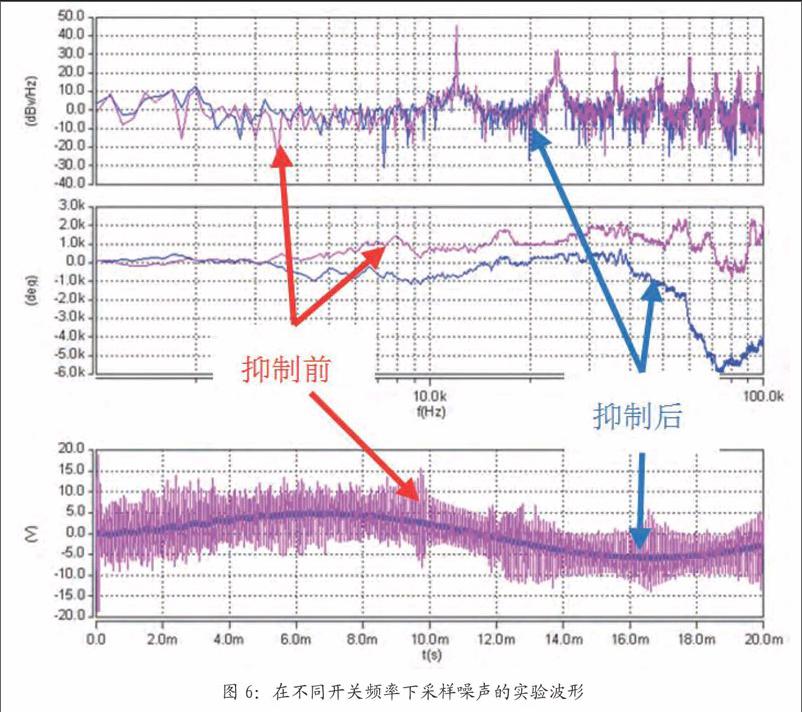
闭环实验波形见图8。从实验波形可以看出,增置共模滤波电容后,采样通路的传导噪声得到了有效的抑制,且逆变闭环输出电压波形稳定。
5 结论
本文针对PWM逆变器产生的共模噪声传导通路进行了详细的分析。共模噪声主要是由开关管与散热器间的杂散电容的充放电作用引起,并通过电压互感器上的杂散电容传递到采样电路。本文在分析等效电路的基础上,采用了一种高频噪声抑制方法,仿真和实验结果的吻合,验证了分析结果的正确性。
参考文献
[1]Ji,Q.,X.B.Ruan,and Z.H.Ye,The Worst Conducted EMI Spectrum of Critical Conduction Mode Boost PFC Converter[J].Ieee Transactions on Power Electronics,2015,30(03):1230-1241.
[2]陈名,孙旭东,黃立培.三相逆变器共模传导电磁干扰的建模与分析[J].电工电能新技术,2012(01):18-21+43.
[3]张晓峰,胡庆波,吕征宇.基于BUCK变换器的无刷直流电机转矩脉动抑制方法[J].电工技术学报,2005(09):72-76+81.
[4]刘勇,赵阳,张宇环.基于Pspice仿真的高频直流变换器的传导EMI噪声关键技术研究[J].南京师范大学学报(工程技术版),2013(01):1-6.
[5]陈锋,曾岳南,暨绵浩.AC/DC Buck变换器的传导干扰分析及抑制[J].机电工程,2006(10):42-43.
[6]裴雪军,张凯,康勇.基于EMI滤波器的逆变器传导电磁干扰的抑制[J].电气传动,2007(12):35-38.
[7]张重远,闫杰,李文峰,基于散射参数的电压互感器高频数学模型[J].电网与清洁能源,2009(02):9-12.
[8]眭晓飞.电压互感器高频无源电路模型建立方法研究[D].北京:华北电力大学,2009.
[9]张元峰,孟进,张向明.三相电力变压器高频传输特性研究[J].电力电子技术,2012(05):22-24.
[10]宋晓婷.高频高压变压器分布参数测量和绕组结构设计[D].大连:大连理工大学,2013.
[11]邵学飞,李威强.浅析高频变压器分布参数的变化趋势[J].电力电子技术,1995(01):44-46.
[12]李佑淮,肖登明,王延安.高频变压器分布参数对逆变电源性能的影响[J].电力电子技术,2008(09):37-38+44.
[13]曾光,金舜,史明.高频高压变压器分布电容的分析与处理[J].电力电子技术,2002(06):54-57.

