柴油机活塞瞬态温度场有限元分析

刘建敏， 何盼攀， 王普凯， 刘艳斌， 韩立军

(1. 装甲兵工程学院训练部, 北京 100072; 2. 装甲兵工程学院机械工程系, 北京 100072)

柴油机活塞瞬态温度场有限元分析

刘建敏1， 何盼攀2， 王普凯2， 刘艳斌2， 韩立军2

(1. 装甲兵工程学院训练部, 北京 100072; 2. 装甲兵工程学院机械工程系, 北京 100072)

利用ANSYS Workbench建立了某高强化增压柴油机的活塞-缸套有限元耦合模型，通过插入命令流的方式完成边界条件的施加，由此得到了活塞的瞬态温度场，在此基础上计算了活塞的瞬态热应力。结果表明：活塞顶面2 mm深度范围内的瞬态温度场波动较为剧烈，但随着深度的增加趋于平缓；顶面瞬态热应力波动达到13.696 MPa，波动幅值较大，对活塞的疲劳寿命造成一定影响。

柴油机； 活塞； 有限元分析； 瞬态温度场； 瞬态热应力

柴油机在正常运行时，缸内的燃气温度和受热部件表面的热流密度呈周期性的变化。由于活塞与高温燃气直接接触，其顶面1～2 mm深度范围内的温度变化十分剧烈[1]，由此产生的瞬态热应力对活塞的疲劳寿命影响较大。因此，对活塞进行应力场和疲劳寿命仿真计算时，单纯地分析稳态温度场已无法保证仿真的准确性。

随着计算机硬件的升级和有限元软件的不断优化，活塞的瞬态传热研究不断趋于成熟，其中多部件耦合传热的方法应用较为广泛[2]。通过活塞-缸套的整体耦合传热分析，将单个部件复杂的边界条件转化成耦合部件的内部导热，不仅提高了计算精度，同时也提高了计算速度。基于此，笔者建立了某高强化增压柴油机的活塞-缸套有限元耦合模型，对其在标定工况下(2 000 r/min)的瞬态温度场进行分析研究，并计算瞬态热应力，得到活塞温度场的波动对活塞热应力的影响规律。

1 传热微分方程

假设部件为常物性导热体，活塞与缸套之间为非稳态导热，则导热方程[3]为

(1)

高温燃气与活塞、缸套之间的传热采用第三类边界条件,即

Φ=hA(tw-tf)。

(2)

式中：t为温度；τ为时间；k为材料的导热系数；ρ为材料密度；c为材料比热容；x、y、z为笛卡尔坐标分量；Φ为对流换热量；h为对流换热系数；tw为物体温度；tf为流体温度;A为活塞与燃气接触面最外层面积。

利用有限元法计算瞬态温度场的一般方程[4]为

(3)

2 活塞-缸套有限元耦合模型

2.1 活塞-缸套的相对位置关系

在活塞瞬态温度场分析中，假设活塞只沿缸套做上下往复运动，忽略其径向摆动，则活塞与缸套的相对位置关系[5]为

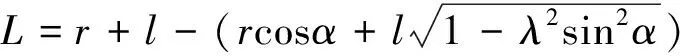
(4)

式中：L为活塞位移；r为曲柄半径；l为连杆长度；α为曲柄转角；λ为连杆比。

2.2 网格划分与边界条件

利用Pro/E软件建立活塞-缸套三维耦合模型，将此模型导入ANSYS Workbench中，并采用Tetrahedrons对三维耦合模型进行网格划分，设定最大网格尺寸为6 mm，最小网格尺寸为2 mm。在划分网格过程中，忽略耦合模型的倒角、圆角等部分细节，并对活塞外表面和缸套内壁面进行相应的细化。图1为划分网格后的活塞-缸套有限元耦合模型剖面，其单元个数为220 518，节点数为376 706。活塞-缸套有限元耦合模型的边界条件如图2所示。

图1 活塞-缸套有限元耦合模型剖面

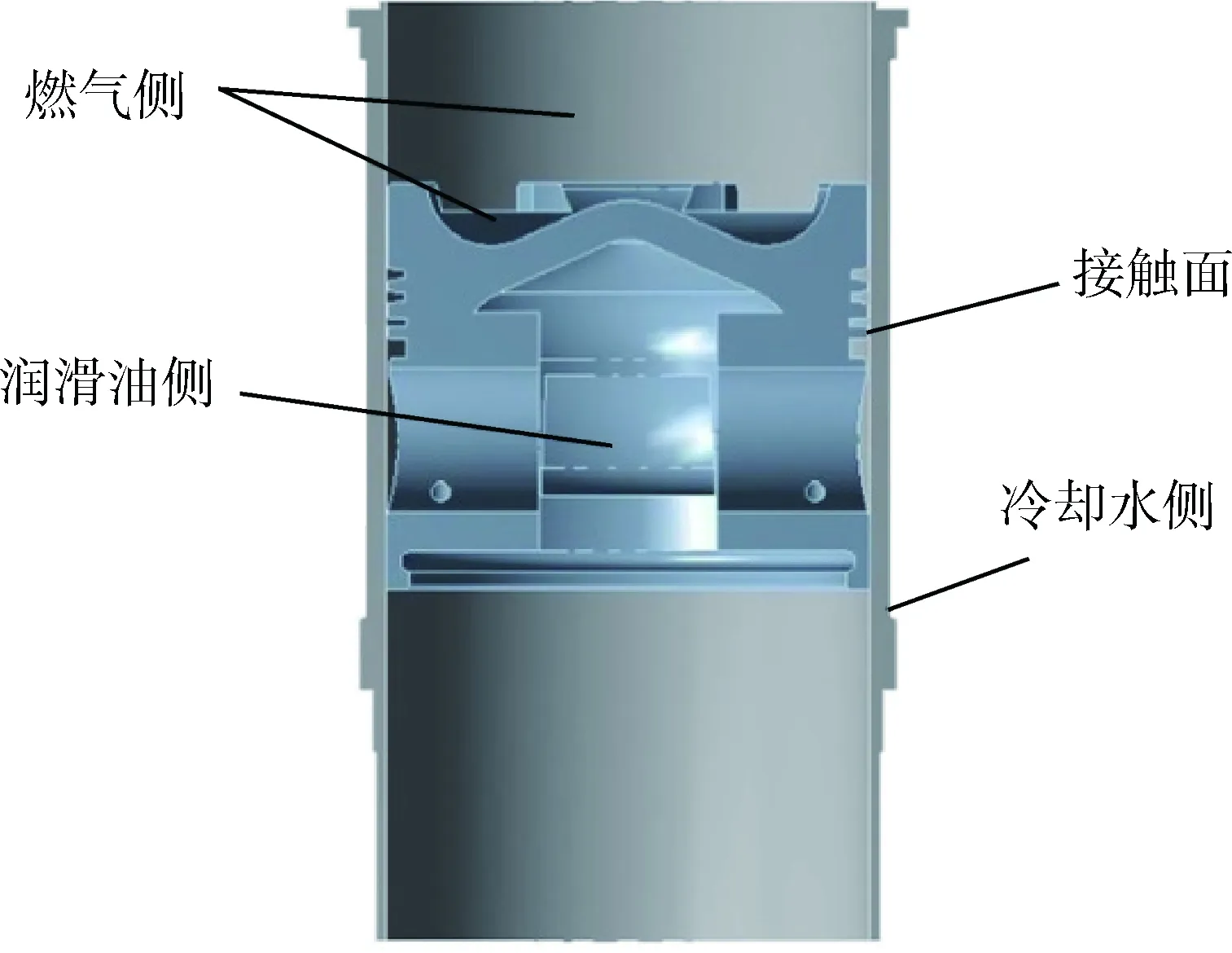
图2 活塞-缸套有限元耦合模型边界条件

3 边界条件的确定

3.1 初始条件

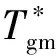
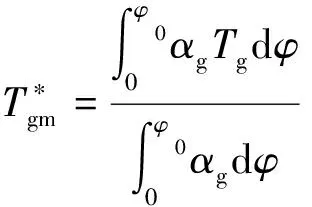
(5)

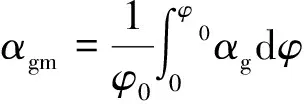
(6)

式中：Tg为燃气瞬时温度；αg为燃气瞬时对流换热系数；φ为曲轴转角；φ0为终了时刻所对应的曲轴转角。

3.2 燃气侧

耦合模型的燃气侧主要包括活塞顶面和与燃气接触的部分缸套内壁面，这2部分与高温燃气之间主要通过对流进行热量交换，因此燃气的瞬时温度和瞬时对流换热系数是计算的关键。基于此，笔者采用零位燃烧模型计算其热力过程，求得燃气瞬时温度；对于高强化的增压发动机，采用Woschni经验公式[6]计算燃气瞬时对流换热系数。其计算结果如图3所示。

3.3 活塞底部

本文研究的柴油机采用机油飞溅润滑的方式对活塞底部进行冷却，其换热系数hoil计算公式为

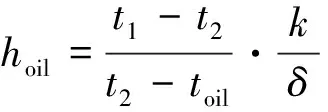
(7)

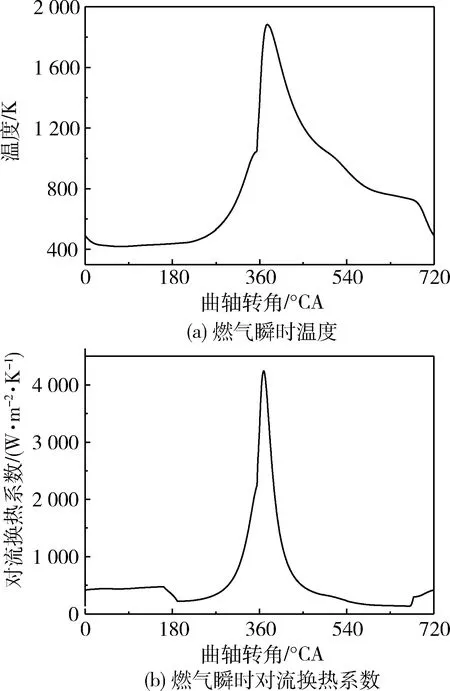
图3 燃气瞬时温度与瞬时对流换热系数

式中：t1为缸内燃气温度；t2为活塞顶面温度；toil为活塞顶下内侧壁面的温度；δ为活塞顶的厚度。

3.4 冷却水侧

气缸套冷却水侧壁面温度沿轴向的变化较为均匀，且与冷却水的温度相近，一般情况下可当作无相变对流换热处理[7]。冷却水的对流换热系数可由努塞尔数确定，而努塞尔数则由迪特斯-波尔特公式计算得到，即

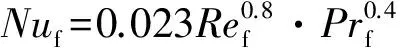
(8)

式中：Nuf为努塞尔数；Ref为雷诺数；Prf为普朗特数。

3.5 接触面边界

活塞与缸套接触面处存在润滑油膜，可将润滑油膜等效成一维热阻施加于接触面处，从而将接触面处较为复杂的边界条件转化为活塞与缸套之间的导热，同时也保证了计算的精度[8]。

4 仿真分析

4.1 瞬态温度场

4.1.1 活塞-缸套瞬态温度场

在进行瞬态温度场计算时，活塞与缸套之间的相对位置及燃气的作用面不断变化，需要准确地确定每个时刻活塞的位移以及换热条件的对应关系。由于在ANSYS Workbench中，瞬态热模块分析范围较为单一，无法实现相关运动学功能。基于此，笔者采用了瞬态动力学模块，在边界条件施加时插入了命令流，以拓展其高级功能，将分析单元更改为SOLID5三维耦合场实体单元，使用其结构-热分析功能，并在后处理中提取温度，从而完成瞬态温度场的直接耦合求解。

以稳态热分析求得的额定转速下活塞-缸套的稳态温度场作为瞬态分析的初始条件。柴油机转速为2 000 r/min时，一个工作循环的时间为0.06 s，瞬态计算采用100个载荷步，则时间步长为0.000 6 s，即7.2 ℃A。经过时间步长的无关性验证，0.000 6 s的时间步长能够达到计算精度。经过计算，得到的活塞上止点时刻(360 ℃A)和最高温度时刻(396 ℃A)的瞬态温度场云图如图4所示。

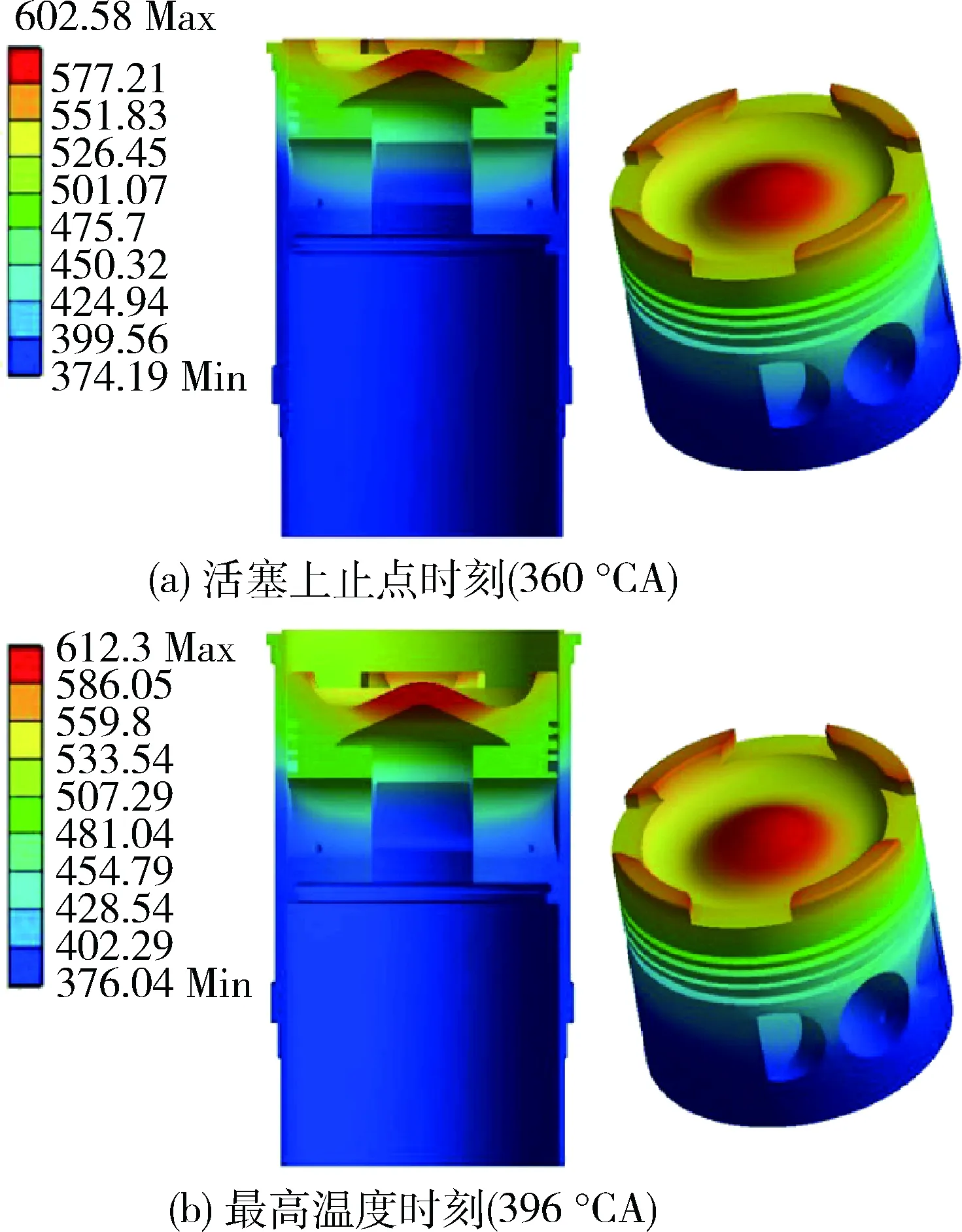
图4 活塞-缸套瞬态温度场云图

由图4可以看出：活塞-缸套耦合模型的温度由上至下逐渐递减，而缸套的总体温度比活塞要低100 K，这是因为缸套外侧冷却水从缸套外壁面带走了大量的热量；同时，由于在做功冲程中缸内的工质燃烧放出大量的热量，使得缸内温度急剧升高，导致活塞表面的温度在短时间内迅速达到最大值。

4.1.2 活塞表层不同深度温度变化规律

图5为活塞表层不同深度处的温度变化曲线。可以看出：在一个工作循环中，活塞顶面温度与缸内燃气温度几乎同步变化，此时的温度波动也最为剧烈(8.79 K)；随着深度的增加，温度波动趋于平缓，当深度>2 mm时，温度波动范围很小(<1 K)；同时受材料热惯性影响，温度波动的峰值也出现了延迟。

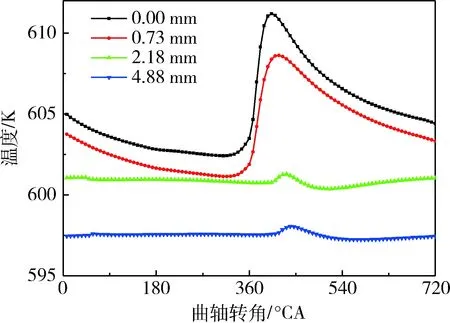
图5 活塞表层不同深度处的温度变化曲线

4.2 瞬态热应力

为了分析温度波动对活塞热负荷的影响，在瞬态动力学模块中对活塞位移、活塞销孔面处沿销孔轴线方向的移动和转动、活塞底面沿活塞轴线方向的移动施加约束，由此求得活塞在一个工作循环中不同时刻的瞬态热应力。

由于每个时刻的最大瞬态热应力均出现在活塞顶部下表面中心处，因此以该处的热应力为标准，对最大热应力时刻(57.6 ℃A)和最小热应力时刻(662.4 ℃A)的瞬态热应力分布云图进行分析，如图 6所示(为便于分析，对活塞顶面中心、顶面边缘和活塞顶部下表面中心3处的热应力进行了标注)。可以看出：活塞顶面中心的热应力波动最大，达到13.696 MPa，顶面边缘处热应力波动为6.450 6 MPa；随着深度的增加，热应力波动幅度不断减小，在活塞顶部下表面处基本保持恒定。

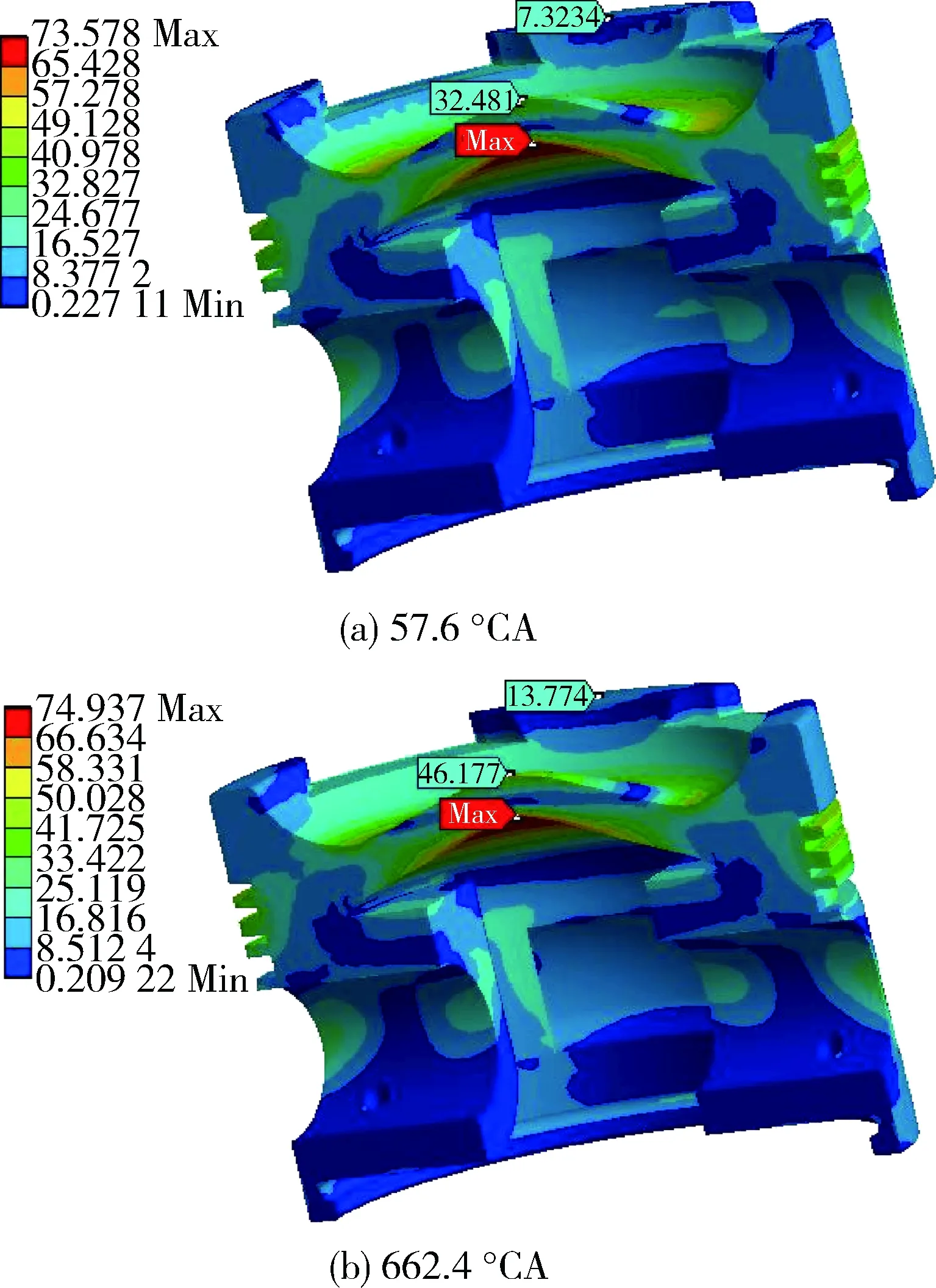
图6 活塞-缸套瞬态热应力场云图

由于活塞工作时还承受交变的燃气压力、销座支反力、侧推力和惯性力等机械负荷，因此需要进行热机耦合分析，以考察活塞实际的应力场分布情况。但因为活塞顶面热应力波动较大，特别是柴油机实际工作时易受外界各种因素的影响而发生改变，活塞顶面有可能产生更大的瞬态热应力，从而导致热机耦合分析的难度也相应增加。

5 结论

利用有限元软件计算了活塞-缸套有限元耦合模型的瞬态温度场，在此基础上得到了活塞的瞬态热应力场。结果表明：活塞顶面2 mm范围内温度场的波动较为显著，最高温度波动达到8.79 K；活塞顶面中心处的应力波动达到13.696 MPa，波动幅度较大，这说明温度场的波动对活塞顶面的热应力有较大影响，是活塞顶面出现疲劳损伤不可忽视的因素。

[1] 原彦鹏，张卫正，程晓果，等.高强化内燃机活塞瞬态温度场分布规律研究[J].内燃机工程，2005,26(4):35-38.

[2] 孙秀峰，冯立岩，许锋.内燃机活塞组有限元分析研究进展[J].车用发动机，2002(10)：10-13.

[3] 杨世铭，陶文铨.传热学[M].北京：高等教育出版社，1998.

[4] 浦光益.ANSYS Workbench基础教程与实例详解[M].北京：高等教育出版社，2013：202.

[5] 袁兆成.内燃机设计[M].北京：机械工业出版社,2008:21.

[6] 姚仲鹏，王新国.车辆冷却传热[M]. 北京：北京理工大学出版社，2001：17-25.

[7] 白敏丽，蒋惠强，陈家骅.发动机活塞组-缸套整体耦合系统瞬态温度场数值模拟[J].小型内燃机，1994，22(4)：12-17.

[8] 高鹏，韩振南.柴油机活塞-缸套的瞬态传热有限元分析[J].矿山机械，2015，43(2):120-125.

(责任编辑: 尚菲菲)

FEA on Transient Temperature Field of Diesel Engine Piston

LIU Jian-min1, HE Pan-pan2, WANG Pu-kai2, LIU Yan-bin2, HAN Li-jun2,

(1. Department of Training, Academy of Armored Force Engineering, Beijing 100072, China; 2. Department of Mechanical Engineering, Academy of Armored Force Engineering, Beijing 100072, China)

A coupling finite element model of certain turbocharged diesel engine piston and cylinder is established by using the software of ANSYS Workbench. The transient temperature filed is obtained by inserting the command flow into the boundary condition, and accordingly the transient thermal stress is calculated. The result shows that the transient temperature field fluctuation is active within 2 mm in depth on the piston top, but the fluctuation decreases with the increase of depth; the thermal stress fluctuation on the piston top reaches 13.696 MPa, the level is higher, which affects the fatigue life of piston.

diesel engine； piston; FEA; transient temperature filed; transient thermal stress

1672-1497(2017)02-0044-04

2017-01-14

国家“973”计划项目

刘建敏(1963-)，男，教授，博士。

TK421+.1

A

10.3969/j.issn.1672-1497.2017.02.010