基于遗传算法的变电站巡检机器人任务路径规划方法研究
王 锐,莫志超,彭向阳,庞小峰,饶章权
(1.广东电网有限责任公司 电力科学研究院,广州 510080;2.中航工业洛阳电光设备研究所,河南 洛阳 471009)
基于遗传算法的变电站巡检机器人任务路径规划方法研究
王 锐1,莫志超2,彭向阳1,庞小峰1,饶章权1
(1.广东电网有限责任公司 电力科学研究院,广州 510080;2.中航工业洛阳电光设备研究所,河南 洛阳 471009)
近年来,随着变电站巡检机器人在变电站中的广泛使用,巡检机器人路径规划问题越来越成为亟待解决的问题;巡检机器人在已知的拓扑地图中标记了待执行巡检任务的停靠点,不同任务需要从初始点出发经过不同的一系列停靠点再返回初始点,如何规划路径是机器人面临的问题;首先分析了路径规划面临的问题,然后通过分析拓扑地图的特征,对地图进行等价简化,再对问题进行建模使用遗传算法求解巡检任务路径规划的近似最优解;通过仿真实验证明,提出的基于遗传算法的路径规划方法是可行有效的,为变电站巡检机器人任务路径规划提供了一种有效方法。
变电站机器人;路径规划;遗传算法;进化算法;中国邮差问题
0 引言
近年来,变电站巡检机器人在变电站巡检中占有了越来越重要的地位。尤其在少人或无人值守的变电站,巡检机器人更是担当了主要角色。巡检机器人巡航时间受到电池影响,如何提高巡检效率成为亟待解决的问题。如何在最短时间内完成所下定的巡检任务成为研究的方向。
巡检机器人在扫描完变电站环境之后会生成一个无向连通拓扑图,在拓扑图的边上会标记有若干的停靠点。不同任务需要从初始点出发经过不同的若干个停靠点再返回初始点。这是一个近似的中国邮递员问题[1]。求解此类问题目前研究有以下几大类算法:1)动态规划算法[2],通过寻求优化的搜索算法求得较优的解;2)模拟进化算法,如蚁群算法,遗传算法,粒子群算法等[3];3)DNA算法[4]。本文通过对问题分析,提出基于遗传算法的解决方法,有效解决了巡检机器人路径规划问题。
1 巡检路径规划面临的问题
1.1 路径规划原理
变电站机器人巡检是按照预先设定好的路径进行行走,在路径上有停靠点,机器人到达停靠点停车进行动作。不同任务会选择不同的停靠点,如何从初始点出发以最短的时间完成任务并返回初始点是本文要研究的目标。由于机器人在停靠点执行动作时间相同,如何以最短的路径代价通过所有停靠点并返回是问题的核心。
机器人巡检路径构成了一个连通无向图[5],如图1所示,表示为G=(V,E),V表示所有路径顶点集合,E表示所有路径集合。使用S表示所有停靠点集合,每个路径包含若干个停靠点。
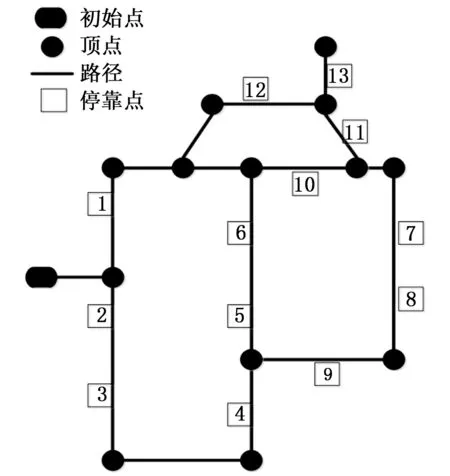
图1 机器人巡检拓扑图
机器人巡检过程中会优先巡检同一条路径上所有停靠点。例如任务中含有2和3停靠点,机器人在从初始点出发,巡视2号停靠点之后一定会先巡视3号停靠点。这与中国邮差问题中经过街道一样。所以可以将机器人巡视要经过的停靠点转换为需要经过的路径。本文将路径上停靠点最小编号作为路径编号。
1.2 路径规划难点
巡检机器人路径规划问题可以总结为求从初始点出发经过图上选定的若干条路径并返回初始点的最短代价。即给定一组待巡检的路径集合{e1…en},求出一个集合排列的顺序使得从初始点出发按顺序经过排列中的路径然后返回初始点的路径最短。2个点之间行走路径按照Floyd算法[6]求解。此问题类似于中国邮差问题[7],路径集合{e1…en}的所有排列有n!个,从n!个排列中找到代价最小的排列在n较大时这几乎不可能。求解最优排列问题可以使用动态规划算法[8],穷举所有可能的解。
1.3 动态规划算法
动态规划算法是求取最优解的一种算法。根据机器人当前位置,在图中进行广度优先搜索,只保留第一层的搜索结果作为下一巡检目标的备选集。将机器人移动到备选集中的一个位置,在此位置再进行广度优先搜索[9],继续移动。如图2所示,当巡检全部停靠点时,从初始点出发,首先搜索到1和2号停靠点,机器人选择1号停靠点,在1号停靠点搜索下一个备选集为2、6、10、12号停靠点,重复此过程,可以将所有可行路线遍历,求出代价最小的路径。
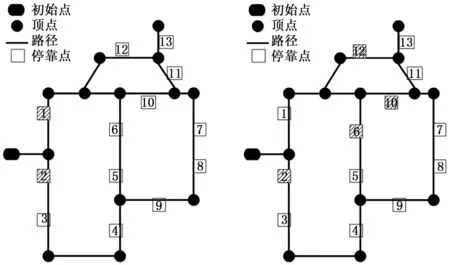
图2 机器人巡检动态规划算法示意图
在问题描述中已说明巡检时会将路径上所有停靠点一次巡检,即巡检2号停靠点是机器人会将3号停靠点巡检。所以在搜索算法中需要搜索的次数为待巡检的路径个数n,每次搜索到的备选集个数约为2~4个。可得算法时间复杂度在2n~4n。在待巡检路径n较多时此算法求得最优解需要的时间是不能忍受的,本文提出了基于遗传算法的求解方法。
2 基于遗传算法的求解方法
首先通过分析拓扑图的特征对拓扑图简化,减少参与计算的路径;再根据动态规划算法给出路径排列的等价模型;最后给出遗传算法的选择、交叉、变异、适应度模型使用遗传算法进行求解。
路径规划方法的具体步骤如图3所示,首先初始化算法:简化拓扑图以减少计算路径,再使用Flord算法计算点到点最短路径和代价并存储到持续存储;然后根据输入任务点序列使用本文提出的遗传算法进行迭代求解;最后输出最优个体作为最优任务序列。
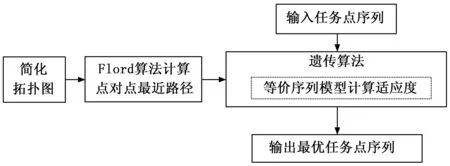
图3 路径规划方法步骤
2.1 拓扑图简化
在机器人巡检拓扑图中存在一些“死胡同”,这些“死胡同”总是需要进入再退出。无论何时巡检“死胡同”内的停靠点,进入、退出的代价是固定的。如图4所示,13号停靠点在一条“死胡同”中,巡检13号停靠点必须从图中空心顶点出发再回到图中空心顶点,这类在“死胡同”内的停靠点在不同的路径集合{e1…en}的排列中的代价是固定的,所以在计算最优排列是可以忽略这些点所在的路径。
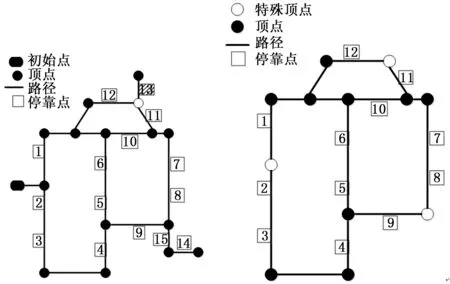
图4 巡检路径简化示意图
具体算法流程:
1)寻找图中度为1的顶点,不存在则结束;
2)寻找顶点所在边的另一顶点(兄弟顶点);
3)将顶点标记到兄弟顶点;
4)删除顶点所在边,返回1)。
如图4所示,左边图经过简化之后变为右边的图。
2.2 路径排列等价模型
路径集合{e1…en}的所有排列组合有n!个,但是其中有很多是无效的巡检序列,例如{e1,e2,e4,e5}集合的一个排列{e1,e4,e2,e5}是一个无效序列,因为从e1到e4的过程必然经过e2,e5中一个。对于{e1,e2,e4,e5},根据动态规划算法可知,在e1下一个巡检路径只能是e2,e5中一个。
在此本文给出一个转换算法,将任意排列转换为符合搜索逻辑的序列。算法过程如下:
1)输入任意排列E={e1…en},元素个数为num。初始化n=1,输出排列R={E(1)},即将输入排列第一个加入输出排列。
2)广度优先搜索寻找E(n)下一步备选集合B={ei…ej}。
3)C=B-R,即从备选集合移除已存在R中的元素。
4)将C中元素按在E排列中顺序排序,将C(1)加入R尾部。n=n+1。
5)若n 6)将E(n)加入R尾部,结束。 例如{e1,e4,e2,e5},e1之后备选集合为{e2,e5},e2在{e1,e4,e2,e5}中顺序靠前选择e2。e2之后备选集合为{e5,e4},e4在{e1,e4,e2,e5}中顺序靠前选择e4。最后得到等价排列为{e1,e2,e4,e5}。 2.3 遗传算法 首先需要给出一个排列序列的代价。本文路径长度计算使用Floyd[10]算法求得每对顶点之间的最短路径,机器人到巡检序列中一个路径代价为机器人从当前位置巡检路径近处的顶点,再将路径上停靠点依次巡检所走的路线总长度。机器人从初始点开始将排列序列所有路径巡视完并按最短路径返回初始点,总路线长度为此排列序列的代价。计算一个排列序列的代价总是计算其有效的等价序列的代价。 遗传算法[11]需要计算每个个体的适应度,此问题中适应度与排列序列代价成反比。本文使用基准对比的方法求得适应度。首先随机一个基准排列序列,求得其代价作为基准代价;任何一个排列序列的适应度为基准代价除以待求序列的代价。将此方法记为f(R),R为排列序列。 选择运算[12]:遗传算法使用选择运算来实现对群体中的个体进行优胜劣汰操作。适应度高的个体被遗传到下一代群体中的概率大;适应度低的个体,被遗传到下一代群体中的概率小。选择操作的任务就是按某种方法从父代群体中选取一些个体,遗传到下一代群体。本文采用轮盘赌选择方法,基本思想:各个体被选中的概率与其适应度函数值大小成正比。设群体大小为n,个体i的适应度通过f(R)求得,记为Fi,则个体i被选中遗传到下一代群体的概率为: 交叉算子[13]作为遗传算法重要的部分,2个父个体通过交叉算子产生带着2个父个体共同信息的子个体。本文采用顺序交叉法作为交叉算子。顺序交叉法为从父代A随机选一个编码子串,放到子代A的对应位置;子代A空余的位置从父代B中按B的顺序选取(与己有编码不重复)。同理可得子代B。如: 父代A: 872 | 139 | 0546 父代B: 983 | 567 | 1420 交叉后: 子代A: 856 | 139 | 7420 子代B: 821 | 567 | 3904 变异算子[14]增加了遗传算法全局搜索能力,避免遗传算法陷入局部最优解。本文采用逆转变异算法,在个体中随机挑选两个逆转点,再将两个逆转点间的基因交换。如14527,随机选择2,4位置交换变异为12547。 本文增加了精英保留策略[15],将最优的个体复制到下一代中。遗传算法具体流程如图5所示。 图5 遗传算法流程图 遗传算法首先要设定结束条件,本文设置结束条件为迭代次数100次和不出现更优秀个体次数10次。当超过设定迭代次数或者超过设定不出现更优秀个体次数没有出现更优秀个体时结束算法。设置交叉概率为90%,即选择的2个父个体有90%就行交叉产生自个体。设置变异概率为1%,每个个体有1%的概率产生随机变异。 为验证本文提出的基于遗传算法求解路径规划的有效性,本文利用仿真手段进行验证。实验数据在visualstudio2015上使用C#编程仿真得到。实验所用拓扑图6所示,路径权重按照最小权重路径归一化结果,如图6中所示。 图6 实验拓扑图 仿真实验测试的机器人任务是巡检停靠点5,6,10,11,12,13,14,15。实验结果如图7所示,随着迭代次数的增加群体评价代价逐渐降低,在迭代20次之后趋于稳定。在迭代30次的群体中取最优个体作为算法的解。本文提出的方法得出的巡检序列为1,12,13,11,15,14,5,6,10;然后返回初始点。巡检代价为65。与使用动态规划求得最优一致,表明本文提出的基于遗传算法的求解方法是迅速且有效的。 图7 仿真实验结果图 本文通过与基于改进遗传算法的机器人路径规划与仿真[16]所提出的算法进行对比,实验结果如图,8所示,实验表明本文通过拓扑图的简化和路径等价模型减少了求解的迭代次数,可以更加迅速地收敛到最优解。 图8 对比实验图 通过实际运行本算法在路径教较少情况下总是能找到最优解,在路径较多的情况下也可以找到比较良好的解,充分满足了变电站巡检机器人任务路径规划的需求。 本文首先分析研究了变电站巡检机器人任务路径规划的问题,将其抽象为路径排序问题。通过分析动态规划算法,得出其时间复杂度高不适用于解决此问题;然后根据变电站巡检路径拓扑图的特点,将图进行简化减少了参与计算的路径个数,减少计算复杂度;再根据动态规划的方式给出路径排列的等价模型;最后建立遗传算法模型对问题进行求解。通过仿真实验分析得出:本文提出的基于遗传算法的路径规划方法有效解决了变电站巡检机器人任务路径规划问题。 [1] 高敬振, 高 勃. 中国邮递员问题50年[J]. 运筹学学报, 2013, 17(1):17-28. [2] 费 蓉, 崔杜武. 中国邮递员问题的动态规划算法研究[J]. 计算机研究与发展, 2005, 42(2):294-299. [3] 严 露. 粒子群算法研究与应用[D]. 成都:电子科技大学, 2013. [4] 李 玮, 王 雷. 中国邮递员问题的DNA计算[J]. 计算机应用, 2009, 29(7):1880-1883. [5] Kay E. Graph Theory with Applications[M]. London: Macmillan, 1976. [6] Floyd R W. Algorithm 97: Shortest path[J]. Communications of the Acm, 1962, 5(6):345-345. [7] 管梅谷.关于中国邮递员问题研究和发展的历史回顾[J]. 运筹学学报,2015,19(3):1-7. [8] Coaker P B. Applied Dynamic Programming[M]. Princeton: Princeton University Press, 1962. [9] Eckstein D M. Parallel processing using depth-first search and Breadth First search[J]. Algorithm Synthesis A Comparative Study, 1977:8-23. [10] 石为人, 王 楷. 基于Floyd算法的移动机器人最短路径规划研究[J]. 仪器仪表学报, 2009, 30(10):2088-2092. [11] 武广号, 文 毅. 遗传算法及其应用[M]. 北京:人民邮电出版社, 1996. [12] 钟求喜, 谢 涛, 陈火旺. 遗传算法中解个体的生存策略[J]. 计算机工程与科学, 2000, 22(1):14-17. [13] 熊 军, 高敦堂, 沈庆宏,等. 遗传算法交叉算子性能对比研究[J]. 南京大学学报:自然科学版, 2004, 40(4):432-437. [14] 邝航宇, 金 晶, 苏 勇. 自适应遗传算法交叉变异算子的改进[J]. 计算机工程与应用, 2006, 42(12):93-96. [15] 朱 灿, 梁昔明. 一种多精英保存策略的遗传算法[J]. 计算机应用, 2008, 28(4):939-941. [16] 李 刚, 鱼佳欣, 郭道通,等. 基于改进遗传算法的机器人路径规划与仿真[J]. 计算技术与自动化, 2015(2):24-27. ResearchofSubstationInspectionRobotpathPlanningMethodBasedonGeneticAlgorithm WangRui1,MoZhichao2,PengXiangyang1,PangXiaofeng1,RaoZhangquan1 (1.Electric Power Research Institute of Guangdong Power Grid Co., Ltd., Guangzhou 510080, China;2.AVIC Luoyang Electro-optical Equipment Research Institute, Luoyang 471009, China) In recent years, substation inspection robot is widely used in substations, but inspection robot path planning problem is a serious problem. Inspection robot has marked task stops in topology map, different tasks require starting from the initial point and through a series of stops and then returns to the initial point, how to planning the path is a problem. First, this paper analyzes the path planning problems, second proposed a map equivalent deformation method by analyzing the topological map features, finally used the genetic algorithm to calculate the approximate optimal solution. Simulation results show the method based on genetic algorithm this paper proposed is an effective method to solve substation inspection robot path planning problem. substation inspection robot; path planning;genetic algorithm; evolutionary algorithm; Chinese postman problem 2016-10-22; 2016-11-21。 王 锐(1988-),男,湖北潜江市人,工学硕士,工程师,主要从事变电站机器人智能巡检及高电压试验研究工作。 彭向阳(1971-),男,湖北黄冈市人,工学硕士,教授级高级工程师,长期从事输电线路及高电压技术工作。 1671-4598(2017)04-0153-03DOI:10.16526/j.cnki.11-4762/tp TP A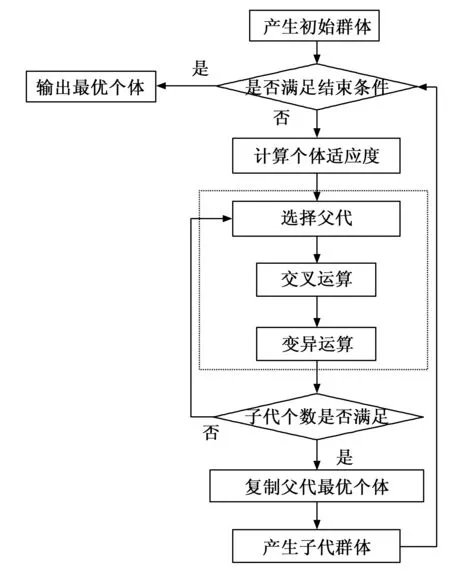
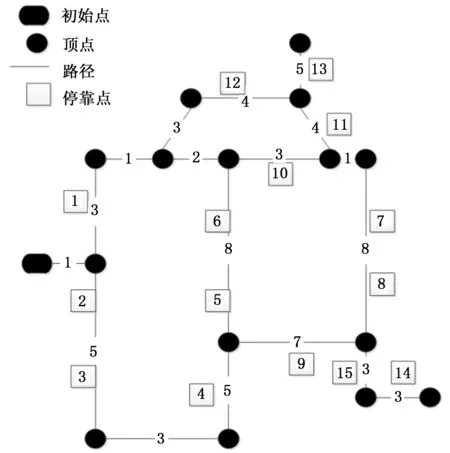
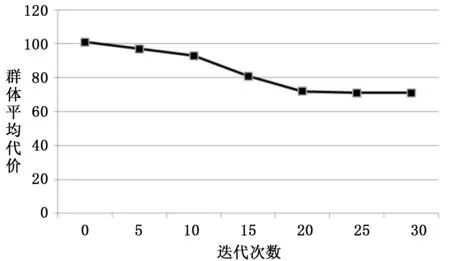
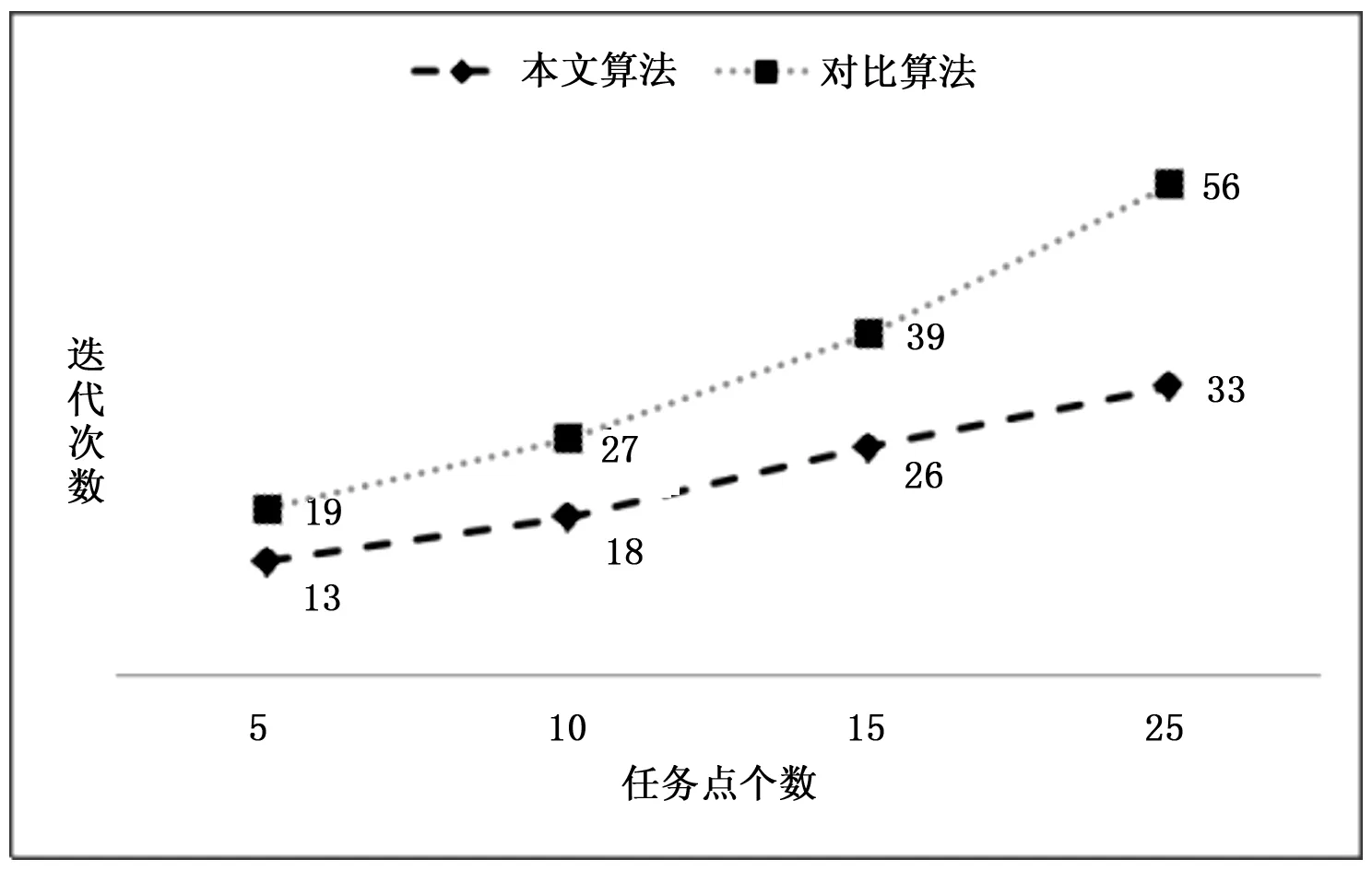
3 仿真实验分析
4 结束语

