Anti-synchronization Between Two Coupled Networks with Unknown Parameters Using Adaptive and Pinning Controls∗

Tian-Tian Sun(孙田田),Shi-Xing Li(李时兴),and Wei-Gang Sun(孙伟刚)

1School of Science,Hangzhou Dianzi University,Hangzhou 310018,China

2School of Mathematics and Statistics,Zhejiang University of Finance and Economics,Hangzhou 310018,China

1 Introduction

Synchronization of complex networks has gained increasing interest over the past decade as a fundamental networked model in understanding the relationship between node dynamics and network topology.[1−3]Since the varieties of node dynamics and network topology,how to realize the considered synchronization is an interesting problem. Presently there have many emerging networked dynamical models,e.g.,introducing time delays,[4]nonlinear and discontinuous coupling[5−6]and white noise.[7]Noted that inner synchronization and outer synchronization[8]are two types of network synchronization.When the synchronization does not appear,the adaptive control,impulsive control,pinning control and sampling data control have been explored to realize the synchronization,see the summarized article.[9]For example,Wanget al.used the M-matrix to study the pinning synchronization of nonlinearly coupled networks with time-varying delays.[10]From existing works on the synchronization,[4−5,7−8,10]the node dynamics and network topology are given beforehand.Recently the synchronization of uncertain networks has been an emerging focus where the node dynamics or network structures are unknown.The research goal is to design the control schemes to identify unknown information in the network model,e.g.,identifying the parameters in the node dynamics and connecting topologies.Wu and Lu[11]investigated the complete outer synchronization between two uncertain networks with an unknown parameter vector of node dynamics,while the network connections inside each network are given.Zheng[12]studied the parameter identification and synchronization of uncertain general complex-variable chaotic delayed networks via adaptive-impulsive control.Liuet al.[13]used a hybrid feedback control to study the parameter identification based on lag synchronization in drive-response networks with unknown parameters.

Outer synchronization was proposed to deal with the dynamics between two coupled networks.Because of diverse interactions between two networks,realizing the outer synchronization is challenging. The pioneering work[8]realized the outer synchronization by open-plusclosed-loop control method.For outer synchronization between two networks with different topological structures,Tanget al.[14]proposed the adaptive controllers.Asheghanet al.[15]studied robust outer synchronization between two complex networks with fractional order dynamics.Compared to complete synchronization,anti-synchronization[16]characterized by vanishing of the sum of relevant state variables widely exists in many chaotic systems. For the networked systems,Wuet al.[17]studied the anti-synchronization between two networks with node dynamics and coupling structures being determined.Wanget al.[18]investigated finite-time anti-synchronization of memristive neural networks with stochastic perturbations.Noted that the above-mentioned works[17−18]on the anti-synchronization employed all the controlled nodes and did not involve the node dynamics with unknown parameters.Usually the known dynamics and topology do not re flect the characteristics of many real networks(e.g., flock of robots)with evolving couplings.

Inspired by the above discussions,we apply the pinning control to reduce the number of controlled nodes.For the coupled networks with unknown parameters in the node dynamics,we design two types of adaptive controllers to realize anti-synchronization.By Lyapunov stability theory,we obtain two theorems on the anti-synchronization.Finally we provide some numerical examples to illustrate the obtained theoretical results.

The remainder of this paper is organized as follows.In Sec.2,preliminaries and network models are shown.Section 3 studies the parameter identification by the adaptive and pinning controls.Section 4 provides numerical examples to show the efficiency of the proposed adaptive schemes.Finally,conclusions and remarks are given in Sec.5.

2 Model Presentation and Preliminaries

Consider the network model between two coupled networks,which is given by

are state variables of networksXandY.εis the coupling strength.The node dynamicsf(x):Rn→Rnis a continuously differential function.The coupling matricesAandBdenote the connection topological structures inside networksXandY,which are de fined as follows:if there is a link from nodesitoj,thenaij/=0,otherwise,aij=0.The entries ofBare de fined analogously.AandBare de fined as outer-coupling matrices with the sum of each row being zero. Γ∈Rn×nis an inner-coupling matrix,which determines the interaction variables.The quantity C(X,Y)(C(Y,X))is the interaction from networkX(Y)to networkY(X).In the original work on the outer synchronization,[8]C(X,Y)is the open-plus-closedloop controller.[19]Generally,we choose C(Y,X)=0,and C(X,Y)=ui,i.e.,the designed controllers.

From existing works on outer synchronization,[8,14]we see that the node dynamics and network topology are known,further they all dealt with complete outer synchronization.Therefore the research goal of this study is to design the controllers to identify unknown parameters in the network model based on anti-synchronization.In reality,determining the system parameters in advance is important for designing robust systems and challenging because the parametrical values vary by some uncertainties.When the node dynamics contains unknown system parameters,Eq.(1)becomes

Throughout the rest of this paper,some useful assumptions and lemmas are presented as follows:

De finition1NetworksXandYachieveantisynchronization if

Assumtion 1Forx,y∈Rnbeing time-varying vectors,there exists a positive constantLsatisfying

where Γ is a positive de finite matrix.

Assumtion 2The nonlinear functionf(x,t)satis fiesf(−x,t)=−f(x,t),i.e.,an odd function ofx.

Lemma 1(Schur Complement[20]).The following linear matrix inequality(LMI)(

whereA(x)=AT(x),C(x)=CT(x),is equivalent to one of the following conditions:

(i)A(x)＞0 andC(x)−BT(x)(A(x))−1B(x)＞0;

(ii)C(x)＞0 andA(x)−B(x)(C(x))−1BT(x)＞0.

3 Anti-Synchronization Between Two Uncertain Networks

3.1 Adaptive Control

In this subsection,we design adaptive controllers to realize anti-synchronization and identify unknown parameters in the node dynamics.The main results are summarized in the following theorem.

Theorem 1Under Assumptions 1 and 2.The antisynchronization of coupled networks(2)with different topological structures(A/=B)is achieved with the following adaptive control schemes:

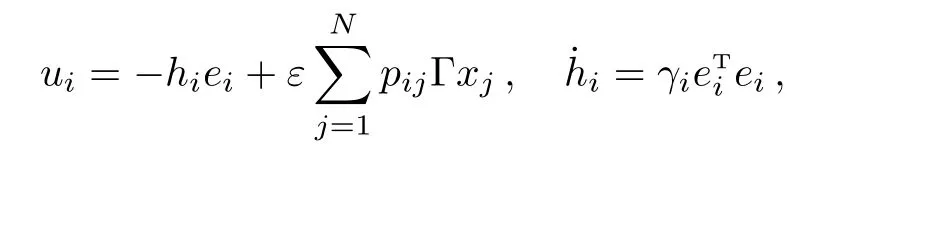
whereγi,ζij,ηi(i,j=1,2,...,N)are arbitrary positive constants.

ProofUsingei=yi+xigives

whereh∗iare suitable positive constants,which are to be determined.

The time derivative ofV(t)along the trajectories of error system(4)yields

Corollary 1When the coupling matrices(A=B)are identical,then the controlleruiis simpli fied as:

3.2 Adaptive Pinning Control

In this subsection,we apply adaptive pinning control to achieve anti-synchronization.The pinning control means that we only control a small fraction of nodes to realize the synchronization of the whole network.In this case,we need that the coupling matricesA,Bare identical and symmetrical.Suppose that the firstm(1≤m＜N)nodes of networkYare controlled;otherwise,rearrange the order of the nodes.The controlleruiis chosen as

The anti-synchronization error of coupled networks(2)reads as

Theorem 2Suppose that Assumptions 1 and 2 hold and the coupling matrix

is symmetric and irreducible.Ifλmax(A2)＜−L/ε,then the anti-synchronization of networks(2)is achieved.

ProofSelect a Lyapunov function as follows,

whered∗i(i=1,2,...,m)are positive constants to be determined below.

Then the derivative ofV(t)along the trajectories of Eq.(5)gives

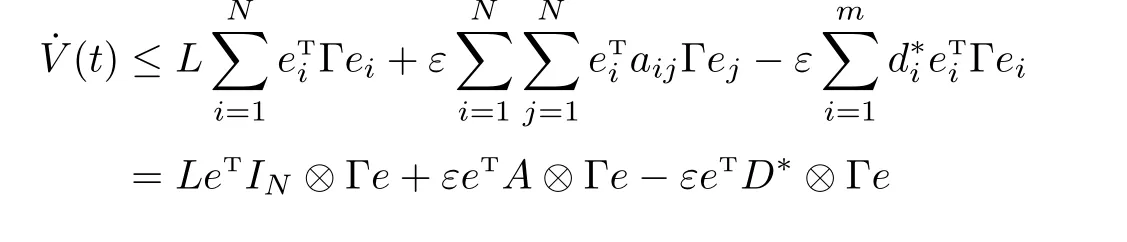
Ifλmax(A2)＜−L/ε,we have Θ2＜0. By Schur Complement,we choose suitable positive constantsd∗i＞synchronization of networks(2)happens.

4 Numerical Examples

In this section,we will provide numerical examples to show the effectiveness of the proposed control schemes obtained in the previous section.In the numerical simulations,the node dynamical equations are taken as the Chua’s circuit,[21]that is,

whereϕ(xi1)=bxi1+(1/2)(a−b)[|xi1+1|−|xi1−1|]anda=−1.27,b=−0.68,α=10.00,β=14.87,θi=1.Since the chaotic attractor is bounded in a certain region and previous results obtained in Ref.[22],the Chua’s circuit satis fies Assumptions 1 and 2.The system can be rewritten in the following form,i.e.,

In what follows,we set Γ=diag(2,2,2)and introduce the quantitiesei1(t)=|yi1(t)+xi1(t)|,ei2(t)=|yi2(t)+xi2(t)|,ei3(t)=|yi3(t)+xi3(t)|,i=1,2,...,N,t∈[0,+∞),to measure the process of anti-synchronization.

4.1 Adaptive Control

In this subsection,we use the control schemes(3)in Theorem 1 to achieve the anti-synchronization and identify the unknown parameter in the node dynamics.The coupling con figuration matrixA=(aij)andB=(bij)are chosen to be

Fig.1 Anti-synchronization errors of ei1(t),ei2(t),ei3(t)by adaptive control.

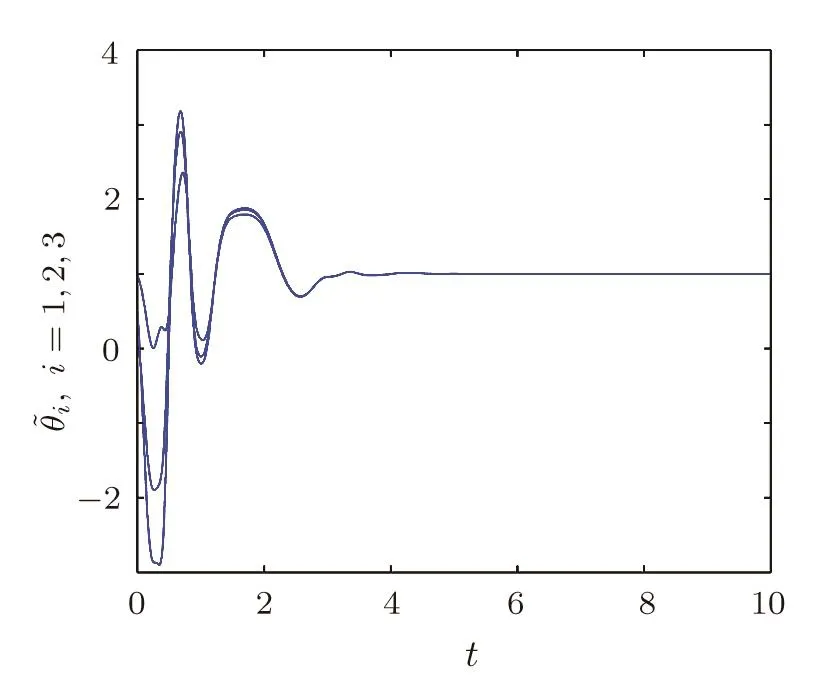
Fig.2Theestimated unknown parameters 1,2,3)by adaptive control.

4.2 Adaptive Pinning Control

In this subsection,we design a pinning control scheme to realize the anti-synchronization.In this case,we choose two identical and undirected coupling matrices as follows:

Fig.3 Anti-synchronization errors of ei1(t),ei2(t),ei3(t)by adaptive pinning control.

According to the obtained results in Ref.[22],we setL=5.7175 andε=5.Based on Theorem 2,we need pin the first three nodes,which satis fiesλmax(A2)＜−1.1435.The corresponding numerical results are shown in Figs.3–4. The time evolutions of anti-synchronization errors are shown in Fig.3.Figure 4 shows that the proposed adaptive controllers and update laws can identify the unknown system parameter.For other pinning schemes,such as low-degree pinning,random pinning,we could calculate the pinning number of nodes using this conditionλmax(A2)＜−L/εwith different values ofLandε.

Fig.4The estimated unknown parameters˜θi(i=1,2,...,10)by adaptive pinning control.

5 Conclusions

The dynamics between two coupled networks has attracted considerable attention,where the designed control schemes for realizing synchronization is important,however the networked system usually has unknown information,how to successfully identify the information is meaningful for designing robust systems.In this paper,we have investigated anti-synchronization between two coupled networks with unknown system parameters in the node dynamics. Besides classical adaptive control,we have designed adaptive pinning schemes to realize the anti-synchronization and obtained the criteria for the pinning number of nodes.Numerical results show that the anti-synchronization is achieved by the designed controllers and the unknown system parameters are fully identi fied. In the future,we will investigate the relationship between dynamics(synchronization or consensus)and topology(e.g.,number of spanning trees[23])in deterministic networks.

[1]S.Boccaletti,V.Latora,Y.Moreno,et al.,Phys.Rep.424(2006)175.

[2]X.F.Wang and G.R.Chen,Int.J.Bifurc.Chaos 12(2002)885.

[3]J.Chen,H.Zhang,L.Qiao,H.Liang,and W.Sun,Commun.Nonlinear Sci.54(2018)202.

[4]G.Al-Mahbashi,M.S.M.Noorani,and S.A.Bakar,Nonlinear Dyn.82(2015)1569.

[5]J.Wang J.Feng,C.Xu,and Y.Zhao,Nonlinear Dyn.67(2012)1635.

[6]S.Zheng,J.Franklin I.353(2016)1460.

[7]Y.Sun and D.Zhao,Chaos 22(2012)023131.

[8]C.Li,W.Sun,and J.Kurths,Phys.Rev.E 76(2007)046204.

[9]A.Arenas,A.D´ıaz-Guilera,J.Kurths,et al.,Phys.Rep.469(2008)93.

[10]J.Wang,J.Feng,C.Xu,et al.,Neurocomputing 177(2016)89.

[11]X.Wu and H.Lu,Neurocomputing 82(2012)157.

[12]S.Zheng,Complexity 21(2016)131.

[13]H.Liu,W.Sun,and G.Al-Mahbashi,Adv.Differ.Equ.2017(2017)122.

[14]H.Tang,L.Chen,J.Lu,and C.Tse,Physica A 387(2008)5623.

[15]M.Asheghan,J.M´ıguez,M.Hamidi-Beheshti,and M.Tavazoei,Chaos 21(2011)033121.

[16]C.Kim,S.Rim,W.Kye,et al.,Phys.Lett.A 320(2003)39.

[17]Y.Wu,W.Sun,and S.Li,Commun.Theor.Phys.55(2011)835.

[18]W.Wang,L.Li,H.Peng,et al.,Neural Process.Lett.43(2016)49.

[19]E.Jackson and I.Grosu,Physica D 85(1995)1.

[20]S.Boyd,L.Ghaoui,E.Feron,and V.Balakrishnan,Linear Matrix Inequalities in System and Control Theory,SIAM,Philadelphia,PA(1994).

[21]L.O.Chua,M.Itoh,L.Kocarev,and K.Eckert,J.Circuits Syst.Comput.3(1993)93.

[22]Y.Wu,C.Li,A.Yang,et al.,Appl.Math.Comput.218(2012)7445.

[23]W.Sun,S.Wang,and J.Zhang,J.Appl.Anal.Comput.6(2016)65.