混凝土重力坝接触爆炸的响应及破坏特性分析
徐强 曹阳 陈健云 李静 刘静
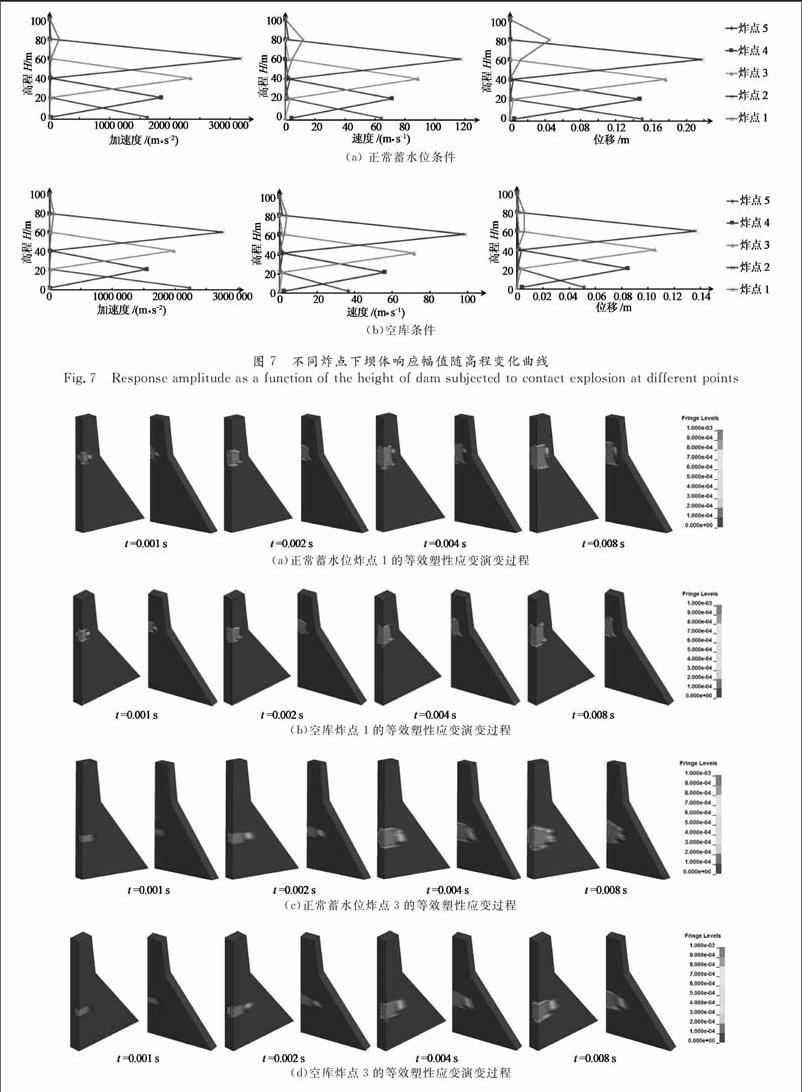
摘要:运用显式非线性动力分析程序LS_DYNA模拟正常蓄水位及空库条件下混凝土重力坝接触爆炸。考虑爆炸荷载作用下混凝土的高应变率的影响,采用HJC(Holmquist-Johnson-Cook)本构模型模拟坝体混凝土的损伤破坏及塑性变形的破坏特性。首先构建炸药空气水混凝土试块模型并对其进行了模型验证。然后构建炸药空气库水坝体地基之间的动态全耦合模型,并对正常蓄水位与空库条件下TNT炸药接触爆炸的大坝动态响应及破坏特征进行了分析。研究结果表明:运用该方法研究混凝土重力坝水下接触爆炸引起的结构动力响应问题,具有稳定的可靠性,弥补了试验研究的不足。正常蓄水位下,在上游布置炸点对坝体的动力响应及损伤程度影响更大,因此在研究大坝抗爆性能时,应重点关注正常蓄水位条件下大坝上游侧炸点水下接触爆炸时大坝的破坏特性。
关键词:混凝土重力坝;HJC本构模型;水下接触爆炸;响应;破坏特性
中图分类号:TV331 文献标识码:A
改革开放以来,国内建设了很多高坝,如已建的三峡大坝、溪洛渡拱坝等。大坝作为水工建筑物的一部分,其安全性是国家安全防护的重中之重。随着现代战争技术与武器的发展,大坝已经成为战争中重要的打击与争夺对象,特别是近年来恐怖袭击频繁,防止大坝结构冲击和研究大坝的抗爆性能至关重要,因此对爆炸荷载作用下的水工大坝破坏特征开展研究具有重大的现实意义。
20世纪末期,随着计算机的发展,对爆炸荷载作用下大坝的数值计算研究迅猛发展。目前,国内对于大坝爆炸荷载作用的研究主要是将理论、实验和数值模拟相结合,并且主要集中在重力坝、拱坝和土石坝方面。在重力坝的研究中,张社荣等采用SPH-FEM耦合算法分析了混凝土重力坝水下爆炸的损伤,用SPH法模拟爆炸点附近的坝体变形破坏,用FEM法模拟爆炸点远处的变形破坏并对水下接触爆炸与非接触爆炸的损伤严重性进行了对比,建立了全耦合模型分析水下爆炸冲击荷载下重力坝的破坏特点;李本平通过模拟炸弹连续打击混凝土重力坝,研究大坝的破坏效应;Yu,徐俊祥和刘西拉对混凝土重力坝水下爆炸建立了全耦合模型,以坝体、坝基、炸药、水、空气为计算域模拟了混凝土重力坝的水下爆炸动力响应。对于拱坝,张社荣和王高辉运用数值全耦合模型,考虑混凝土高应变率效应,采用三维有限元法分析了水下不同位置爆炸冲击荷载下高拱坝的破坏模式,并针对重力拱坝的结构特点分析了大坝在水下爆炸荷载作用下的破坏机理。考虑土石坝的爆炸破坏,刘军等运用显式非线性动力分析程序LS-DYNA对爆炸荷载作用下的大型土石坝进行了数值模拟计算,土石坝在爆炸荷载作用下,在爆炸接触部分发生局部破坏;宋娟等运用共节点算法、接触算法和任意拉格朗日欧拉(ALE)算法模拟了土坝中的爆炸,并且考虑了黏性边界、三维一致黏弹性边界和远置边界,分别模拟计算了3种算法及3种边界下的破坏特性,并对结果进行了比较分析。童桦、罗松南等对应力波在混凝土中的传播进行了研究。
随着碾压混凝土技术的发展,国内已建成许多混凝土重力坝,其安全也是水利工程的核心问题。大坝遭到爆炸袭击,必然造成巨大的灾难,对于混凝土重力坝工程结构的防护和对其抗爆性能的研究逐渐引起关注。重力坝爆炸荷载作用下的破坏按空间位置分为水下爆炸、库区近空爆炸、坝体爆炸。研究表明,水下爆炸比其他爆炸形式具有更大的破坏性,水下爆炸根据炸心距的不同也会对大坝产生不同的损伤破坏。对于水下爆炸的研究已有很长的历史。1948年Cole R H出版的《水下爆炸》分析了水下爆炸的机理,并推导了水下爆炸冲击波超压计算公式,得到广泛的理论与实践运用。近代,随着计算机计算能力的提高,水下爆炸研究在数值模拟方面得到了迅速发展,已经成为重要研究方法之一。
本文运用显式非线性动力分析程序LS-DYNA模拟混凝土重力坝水下爆炸。考慮爆炸作用荷载下混凝土的高应变率,通过在上下游不同位置设置炸点,分析上游水库正常蓄水位和空库爆炸时混凝土重力坝的损伤破坏、结构动力响应及其抗爆性能,为混凝土重力坝的抗爆安全评估和抗爆防护设计提供理论参考。
1坝体混凝土及坝基岩体本构模型
1.1坝体混凝土本构模型
HJC本构模型是一种率相关混凝土本构模型,综合考虑了混凝土材料的大应变、高应变率及高压效应。HJC本构模型用等效强度取代静态屈服强度,如图1(a)所示,HJC屈服方程如式(1)所示。
(1)式中:σ*,p*为量纲为1的标准化等效应力和标准化静水压力,它们是由实际等效应力和静水压力除以材料的准静态单轴抗压强度fc'得到的;A为混凝土材料标准化的凝聚力强度;B为混凝土材料标准化的压力硬化强度;C为混凝土材料的应变率系数;N为混凝土材料的压力硬化指数;D为混凝土材料的损伤度,其中0≤D≤1;p为静水压力;ε*为混凝土材料的特征化应变率,其值为真实应变率ε与参考应变率ε0的比值。
材料的损伤累积用损伤度D来表示。材料的损伤累积主要来自于等效塑性应变、塑性体积应变和静水压力的影响,如图1(b)所示,HJC损伤演化方程如式(2)所示。
(2)式中:△ε0,μp分别为一个计算循环周期内的等效塑性应变和塑性体积的应变增量;εfp,μfp分别为常压下破碎的等效塑性应变和塑性体积应变。
混凝土损伤常数EF,min是混凝土破坏时允许的最小塑性应变,满足式(3)。
(3)式中:D1,D2为材料损伤常数;T*=T/f'c表示的是材料所能承受的标准化最大拉伸强度,T为材料的最大拉伸强度。