Dynamic Weapon Target Assignment Based on Intuitionistic Fuzzy Entropy of Discrete Particle Swarm

Yi Wang, Jin Li, Wenlong Huang, Tong Wen

1 State Key Laboratory of Astronautic Dynamics, Xi’an 710043, China;

2 Northwest University School of Information and Technology, Xi’an 710127, China

3 Air Defense and Antimissile Institute, Air Force Engineering University, Xi’an, 710051, China

* The corresponding author, email: wangyi_kgd@sina.cn

I.INTRODUCTION

WTA (Weapon Target Assignment), a kind of NP（Non-deterministic Polynomial） problem, belongs to nonlinear integer programming[1], with characteristic being discrete, dynamic, nonlinear, random, and having large-scale solutions.The most frequently–used intelligent algorithms are Genetic Algorithm [2], Particle Swarm Optimization Algorithm [3], Differential Evolution Algorithm [4], etc.Compared with traditional methods, intelligent algorithm is apparently superior when solutions are more than 50,000.For some large scale 0-1 knapsack problems,it is hard to get the optimal solutions, while for target assignment and multiple-attribute decision making, sub-optimal solution is just required when they it meets certain demanding index [5].Therefore, this paper aims to take optimal solution as a standard for solution algorithm evaluation.

Kenndy [6] presented DPSO which is based on basic particle swarm optimization algorithm, aiming to solve the 0-1 knapsack problem.Even though DPSO can identify the scope of optimal value solution, it often has problems of convergence-slow and convergence-free when solving large scale or complicated discrete problems.In view of this, domestic and abroad scholars has tried to improve it [7-9].Paper [7] proposes a disturbance mechanism to control the diversity of particle swarm, but the result is always local optimal value.In order to solve the problem of discrete and combinatorial optimization,paper [8] puts forward an improved DPSO,which can effectively reduce the divergence of swarm searching and speed up convergence.So, it is more likely to obtain the local optimum.With mutation and crossover operator of genetic algorithm, paper [9] advances a multi-criteria minimum spanning tree DPSO in purpose of solving the problem of local optimal value.

Considering the deficiency of DSPO, this paper combines intuitionistic fuzzy set theory and DSPO together, and introduces intuitionistic fuzzy entropy as a basic parameter for measure and velocity mutation.Through designing two sets of improved IFPSO, it is expected to solve the pseudo random problem of DPSO in final searching stage, and intensifies the ability of searching global best value, which provides a new method to effectively solve the large scale integer programming problem such as 0-1 knapsack problem and WTA problem.

I.INTUITIONISTIC FUZZY ENTROPY AND DPSO ANALYSIS

2.1 Intuitionistic fuzzy entropy

Fuzzy entropy is measure for fuzzy degree of fuzzy set A.The entropy of a fuzzy set can be taken as a reflection.Takefor example, as to all the fuzzy sets on X,E:.Intuitionistic Fuzzy Sets (IFS),presented by Atanassov [10], is a great development of fuzzy theory by Zadeh (ZFS).IFS adds a non-membership function which considering membership degree, non-membership degreeand hesitating degreeso as to depict the objective world more precisely.IFS surpasses ZFS in expressing ability and reasoning accuracy, so it arouses many scholars’interests [11-13].

This article proposes Intuitionistic Fuzzy Entropy of Discrete Particle Swarm Optimization (IFDPSO) and makes it applied to Dynamic Weapon Target Assignment (WTA)

Intuitionistic Fuzzy Entropy (IFE) is an extension of fuzzy entropy theory, and it is of superiority in describing particle swarm state and its relationship with energy change.Therefore, it has been applied to analyzing the swarm change of DPSO [14].Here, take IFE as a measure for particle swarm, and resume there is an effective region with a radiusRin the center of each particle’s best location.And it is supposed that all the particle in this effective region gather around the region; particles out of the effective region should not gather around here and they are isolated points.

Definition 1Choose the best location of each particle in different generations as aggregating pointi(i=1,2,…N), and set the distance for each particle to getibeDkj,(k=1,2,…N).Therefore, the radius of the effective regionRi=K*max(Dkj), whereKis a random number among [0,0.5].

Definition 2Define that in generationt,if particlek’sDkjRi,the particle are called as “isolated point”, and all the particle countersTxare requested to add 1.Based on this, we can get

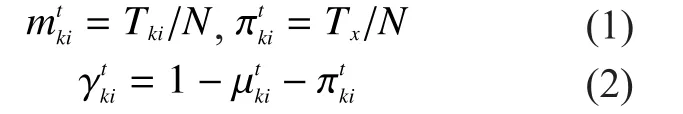
Definition 3In generationt, based on the IFE in paper [15],Etcan be defined as :

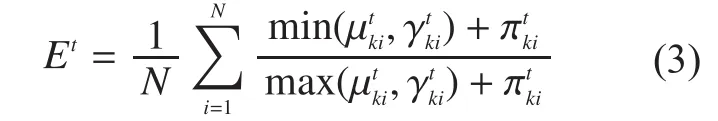
Here,Et→[0,1].

2.2 DPSO Solution Procedure Analysis on 0-1 Knapsack Problem

Based on BPSO [6], DPSO can convert velocity mutation to the possibility value of position mutation by Sigmod function, the formula is as follows:

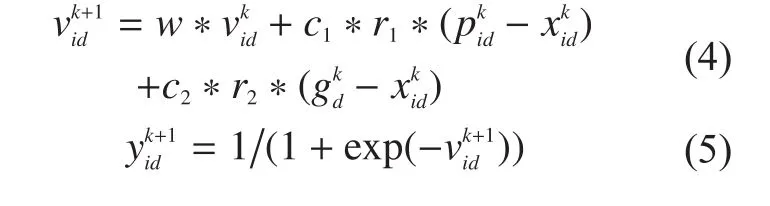
Fig.1 Viriation of DPSO in any two-dimensional velocity mean

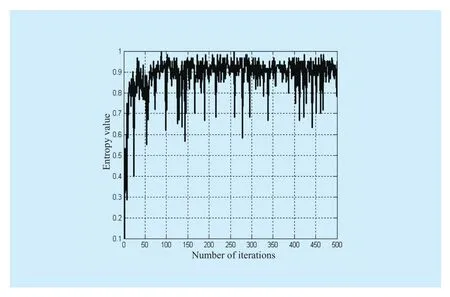
Fig.2 Relative variation of IFE

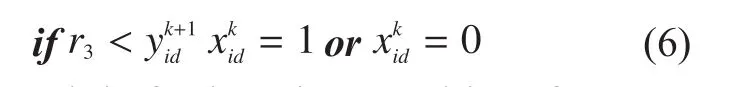
Here, k is for iterations, and k+1 for present iteration; w represents inertia weight, w<1, which is mainly balancing the global and local adjusting ability of algorithm; c1 and c2 are respectively represent the social cognition parameter and individual cognition parameter of particles.Generally, w, c1 and c2 are all non-negative real numbers, and r1 and r2 are random numbers in 0～1.

In view of the characteristics of BPSO and DPSO, it is known that swarm activity directly influences the effect and final result of algorithm searching.So, in this paper, IFE is used to be the measure of swarm activity.Through the analysis of small-scale 0-1 knapsack problem, we can see that the particles’position mutation in interaction process can be reflected by velocity mutation of intuitionistic fuzzy swarm entropy and particles in different dimensions.At the early stage, DPSO adopts two-way initiation and computer simulation to show the variation of all the particles in any two-dimensional mean and the relative variation of IFE.As shown in figs.1-2.

From fig.1, the dimensional velocity fluctuates around certain stable value after 50 times of interaction process.At this time, the entropy is stable.At the initial stage, the velocity mean is over 6, and after the conversion by Sigmod function, the variation of most particles in each dimension is 1.Since velocity decay usually takes some time, and the particles keep in a high state of aggregation, so the entropy stays low even though the velocity is big, as shown in fig.2.With the velocity decay and randomization of particles, the variation of particles in each dimension is relatively average and entropy stays in a high level.At this time, the whole particle swarm is in an active state, so, velocity can’t decay to 0 but fluctuates around a certain value.From fig.1, it can be seen that the value stays around ±1.5, and vitiates between 0.4～0.6 , as the final stage of IFE shown in fig.2, which indicates that velocity exerts an stimulating and restrictive functions on IFE.

Based on the above analysis, we can get that the variation of IFE reflects the active degree of particle swarm, that is variation of system energy caused by the swarm.In the final solution stage of DPSO, the velocity decay of particles enhances the distribution probability of particles in each point, which also enhances the probability of searching the optimal value.On the other hand, the fluctuation of velocity retain stable and in a limited range.That is to say, among a certain quantity of iterations, position mutation of particles in a certain dimension can’t be great, which makes the system energy fluctuate at a high level and so do IFE.However, it is not a real global searching but a pseudo-random searching, which makes the algorithm fail to explore the neighborhood of optimal value.So the point of this paper is to improve DPSO in local exploring in order to make sure this algorithm search better solutions in limited iterations.

II.DPSO BASED ON IFE

Through the solution procedure analysis of DPSO, we can see that the key of improving the algorithm is to effectively control the velocity so as to make it explore in practicable range.In view of this, two improved IFDPSO(Discrete PSO Algorithm based on IFE, IFDPSO) schemes are put forward.

3.1 Two improved IFDPSO schemes

Scheme 1:change the basic velocity iteration method of DPSO to:

Here we adopt velocity mutation mechanism to avoid the stagnation of the algorithm in the final stage of searching.Based on the fluctuation of entropy, we can get the entropy difference of iterationtand setvelocity mutation formula 1as :

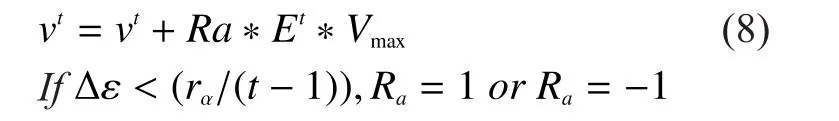
Scheme 2:In view of above analysis, it is known that the final stage searching of DPSO can find the sub-optimal solution only when time is enough.Therefore, it is necessary to enhance the local exploration of DPSO.When swarm entropy rises, it is time to conduct velocity fluctuations for all the particles to search for their neighborhood, leading some particles to get around the global optimum, which enables the particles to find the result closer to the global optimum.Here, we adopt iteration formula (4) and employ velocity mutation mechanism and position mutation strategy.

（1） Velocity mutation mechanism:setvelocity mutation formula 2as :

（2） Position mutation strategy:letbe fitness of particleand global optimal value beIfthe position information of this particle will be updated to the global optimal value with unchangeable velocity information, and the number of mutation particles should not surpass half of swarm.

3.2 Process of IFDPSO

For the purpose of clear elaboration of the process, we choose IFDPSO1 in scheme 2 as an example because IFDPSO in scheme 1 doesn’t adopt position mutation strategy and the rest procedures are same to IFDPSO1.

Step1:Swarm initiation.According to the velocity and position of particles under constraintandsetas stagnation index,as stagnation generation number, andE0as initiation entropy.

Step2:to update the velocity and position of particles in accordance with iteration formula (4)-(6), and update the historical optimal valueand global optimal valuebased on evaluation function, with constantly comparing present global optimal valueand the previous iteration optimal valueIf they are not equivalent, keep updating particles; if equivalent, thenand keep updating and recordof each generation.

Step3:ifand entropythen it is time to take position mutation strategy and initiation for velocity, whereis a measure for the diversity of swarms; if, it is supposed to adopt formula (9)for velocity mutation.

Step4:ifEkdecays fast in the early stage,andit is required to have a reverse operating for velocity in each dimension or do initiation again.

Through variation of entropy, the two schemes of IFDPSO can monitor swarm activity to get the regulation of it and identify the changes in exploring process.The former can guarantee the diversity of particles in different dimensions by two cognitive adjusting parameters and velocity mutation mechanism;the latter can change the state of swarms so as to make sure searching quality of swarms by velocity mutation mechanism and position mutation strategy.Different from the situation that velocity of particles gradually decays in DPSO, IFDPSO is superior, which can make velocity mutation of particles more random,so particles can be distributed to more positions, at the same time the increasing velocity of particles also stimulate the whole swarm to be better in local exploration.Moreover,compared with the pseudo-random searching of DPSO, IFDPSO can monitor the operating results of each generation, and adopt position mutation mechanism and inferior solution particle replacement to regulate swarm variation,so as to make sure the proportion of particle searching other positions in the final stage of solution and avoid the problem of local optimal value caused by velocity mutation to get better solution.

3.3 IFDPSO Solution on 0-1 knapsack problem

The solution object in this paper is 0-1 knapsack problem in integer programming.Since the number of alternative solutions is growing exponentially with the increase of problem scale, so random searching is the most effective solution.But it is difficult to get a better result in limited iterations.Take 0-1 knapsack problem for example, qualityciand pricepi(i=1,2..n) are randomly generated between1～100, wherenrepresents item types,and knapsack capacity is 0.8 times the total mass.Here is the basic knapsack problem model:

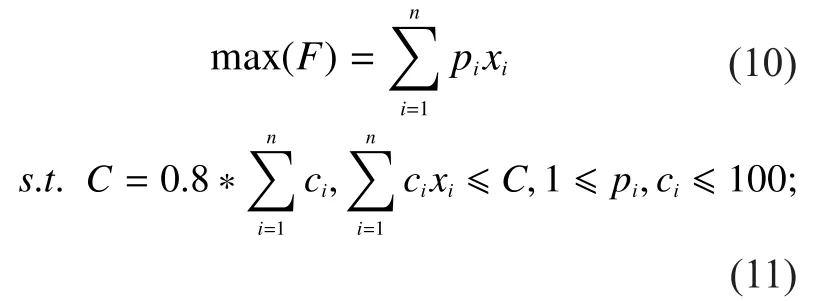
Convert constraints to penalty function,then formula (10) can be set for minimum solution as follows,

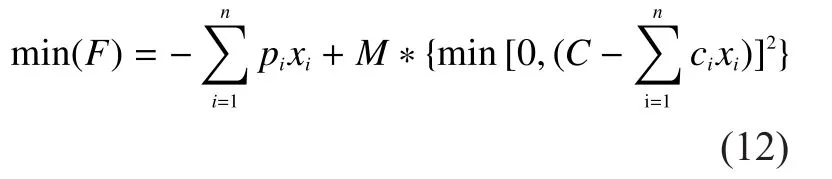
Here,Mis penalty function.X=(x1,x2…xn)represents vector, wherexi=0 or 1,i=1, 2, …,n,Mis a big positive number.

For the sake of observing the effect of velocity and position mutation on algorithm performance, two derivative algorithms for IFDPSO are designed.

Derivative algorithm 1:convert velocity mutation 1 to velocity mutation 2, and then put it to IFDPSO1 in which position mutation has been removed.Here mark it as IFDPSO2.

Derivative algorithm 2:set IFDPSO as IFDPSO3 to observe the effect ofeoon IFDPSO.Makeand the number of particles in each mutation must be a half of whole swarm.

Therefore, formula IFDPSO and IFDPSO1～3 can be generated.There is no need for parameter setting of IFDPSO, andis generated randomly in each generation; parameter setting for position mutation of IFDPSO1 issetfor IFDPSO1 and IFDPSO2; setfor IFDPSO3 and make it a must that the number of particles in each mutation must be a half of whole swarm.

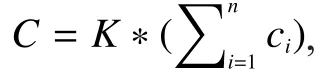
Table 1and table 2 reveal the relative data of 5 types of DPSO in the solution of large and medium scale, and fig.3 shows 5 types of DPSO on n=200 knapsack problem, which is divided into two for better observation.When problem scale increases from 40 to 200, the IFDPSO and IFDPSO1～3 are clearly superior to DPSO.From table 1, we can see that the series of IFDPSO can find the optimal value 1.8108e+003 in limited iterations on n=40 knapsack problem.From the result of solutions, it is clear to see that the performance of IFDPSO is the best while DPSO is the worst.Comparing IFDPSO1and IFDPSO3, it can be found that the fluctuation of IFDPSO1 is big,so the performance is inferior to IFDPSO3,and the only difference in setting iswhich can show the effect ofon solution.Wheneo=0.5, most particles are to be converted and then gathered in the neighborhood of present optimal value after velocity mutation.If mutation frequency is high, the optimal value searched by particles is limited in neighboring small range.In view of this, IFDPSO3 adoptseo=rand/t,which randomly decreases astincreases, so, it just works on part of particles that are far from the optimal value, especially in the final searching stage.Since IFDPSO2 employs IFDPSO in velocity mutation 1, so itis possible for velocity to occur big jumps in the late stage, which enables searching mechanism switch between global and local searching so as to get better solution than that by DPSO.It is close to IFDPSO3 in performance.

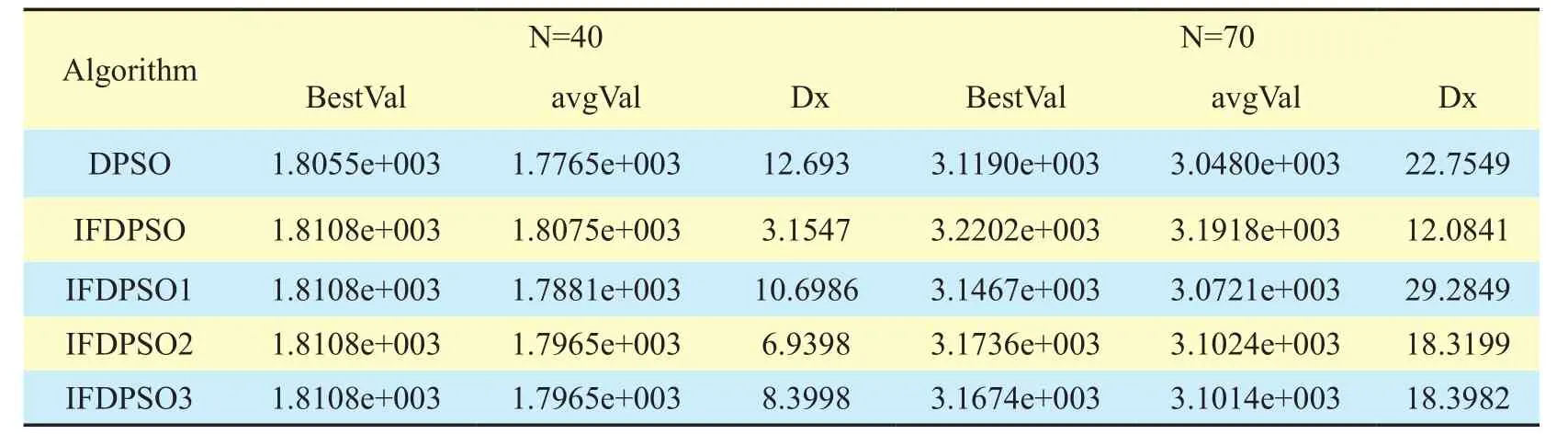
Table I Performance of all types of DPSO on low and medium scale 0-1 knapsack problem

Table II Comparison of all types of DPSO on large scale 0-1 knapsack problem

Fig.3 Performance of DPSO,IFDPSO,IFDPSO1～3 on n=200 knapsack problem

Table 2 shows that in solution of such asn=110, 200 big scale knapsack problem,the performance of IFDPSO is much better than other types of DPSO.Similar ton=70 knapsack problem, the performance of these algorithms is becoming poorer as the scale of problem is getting larger.Because the practical range of random knapsack problem is relatively large, so, IFDPSO has more advantages in positioning this range and deep exploring better results close to optimal value.Especially, the larger scale, the better performance.As it shown in fig.3(1)(2), there is an obvious derivation in the solution curve of IFDPSO from other DPSO algorithms, which indicates that IFDPSO is likely to find the result close to optimal value in the solution of large scale 0-1knapsack problem.

In conclusion, IFDPSO proposed in this paper is of many advantages.It takes IFE as measure for swarm and basic parameter for velocity mutation.With combination of position mutation strategy, two schemes of IFDPSO have been set up and four types of improved IFDPSO and IFDPSO1～3 have been designed,which have effectively solved the pseudo-random searching problem of DPSO in the final stage.And its strong capability of local exploration makes sure the IFDPSO possibly search as much as possible sub-optimal positions and its neighborhood, and intensifies the algorithm ability for searching global optimal value.The experimental data prove that a series of IFDPSO algorithms are more effective than DPSO especially in the solution of large scale problem (0-1 knapsack problem), which provides a new approach for WTA as NP problem with characteristic of being discrete, dynamic,non-linear, random and having huge solution space.

IV.IFDPSO BASED ON WTA

4.1 WTA problem setting

Similar to large scale 0-1 knapsack problem,it is also impossible to predict the optimum in the solution of WTA.Almost all the algorithms can only find approximate solutions,and there are more uncertainties under the real battle circumstance.Therefore, the paper only focuses on testing the performance of IFDPSO on WTA model in range of

4.2 WTA model setting

Based on WTA problem setting and basic WTA model [16], we propose a new improved WTA model, concerning that shifting firepower of fire unit for attacking targets is a dynamic process, marked aswhich is jointly decided by time and resource constraints of shifting firepower.

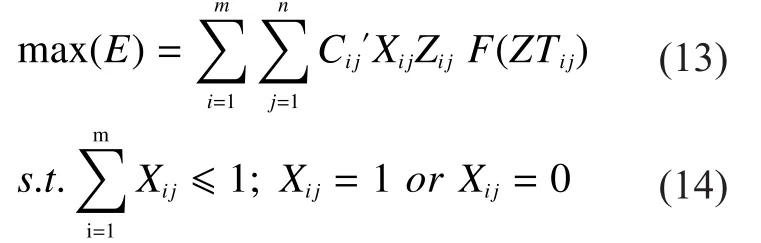
Once the target of shifting firepower is changed, the assigned sequence of shifting firepower is supposed to be changed as well,so formula (13) needs to be recalculated.Moreover, it takes time for sequence allocation if there are too many targets.So, it should be taken into consideration that how to intercept multiple-batch targets in the rangeHere is new model:

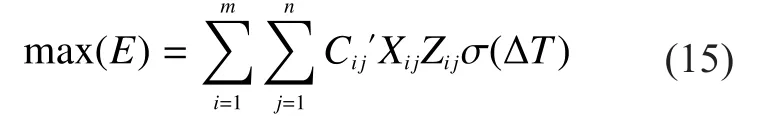
4.3 WTA experiment and result analysis

Based on what we have mentioned above, we get that each assigned fire unit can only shoot one target, and there is constraint for every target, shown in formula (14).There formula(15) can be converted to the followings:

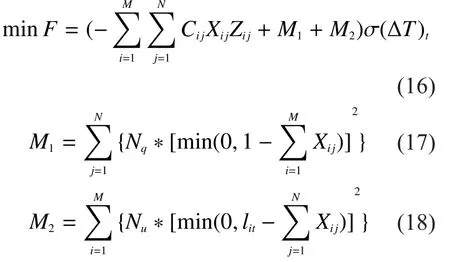
Here, formula (16) represents a converted evaluation function,means assignment calculation should be conducted in the number.Formula (17) and formula (18), as two constraints of formula (16), indicate that each target can be shoot by only one fire unit and the targets of every fire unit should be no more than spare target passagesin the numbertM,Nrespectively refer to fire unit and its shooting targets, andare big enough positive numbers.Formula (16) approximately can be taken as a knapsack problem.When all the fire units can shoot all the targets, thenwhich is a limiting case.

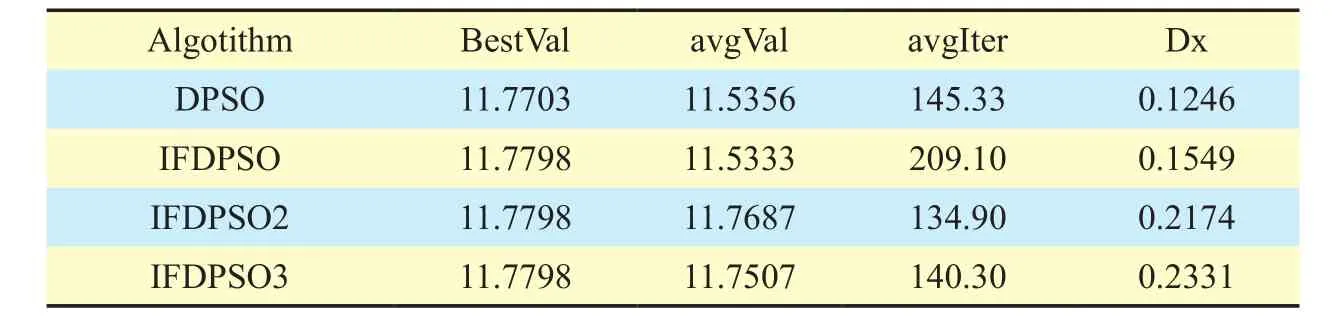
Table III Relative data for four serial DPSO algorithms in the solution of WTA problem

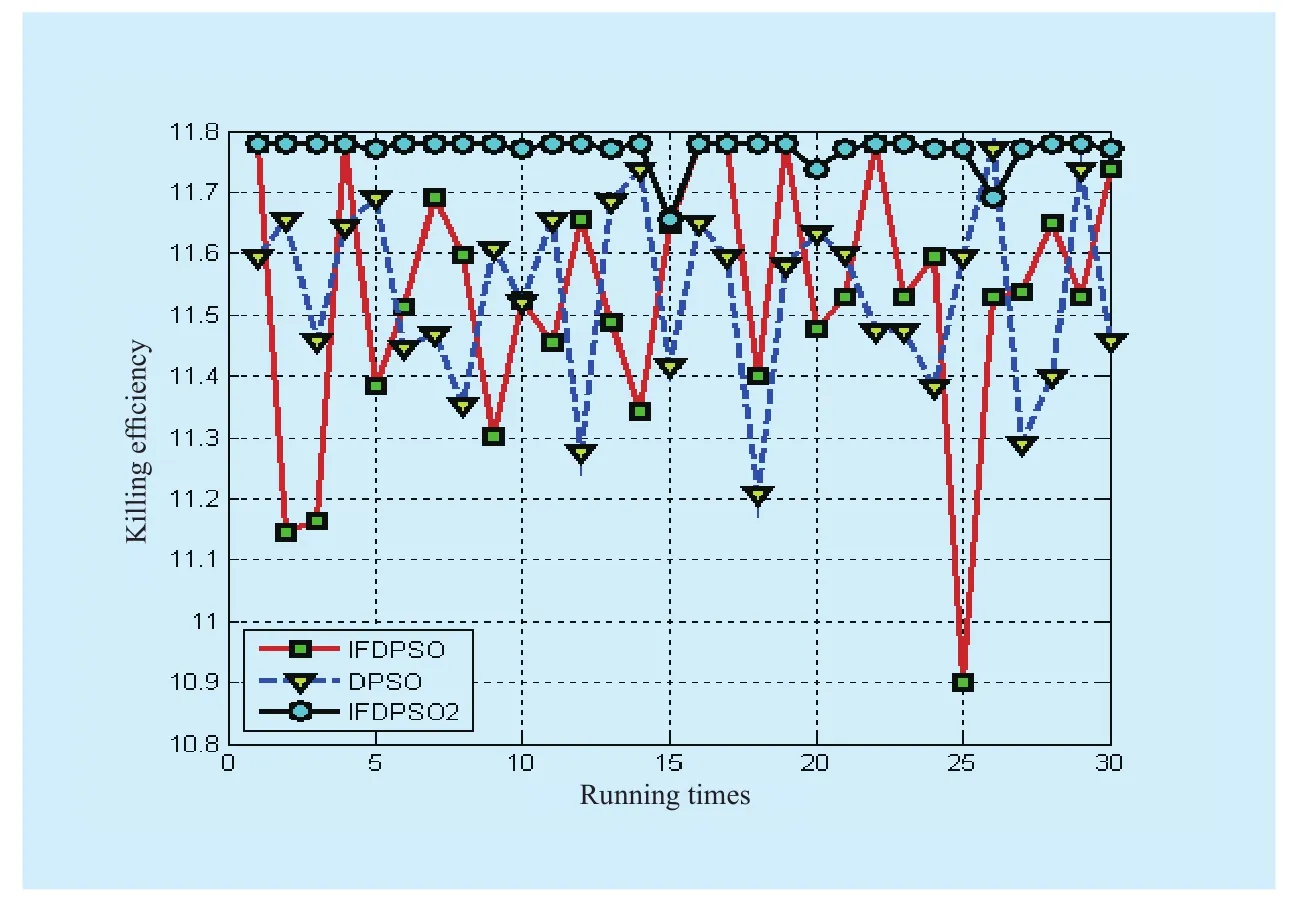
Fig.4 Three DPSO algorithms performance on WTA problem

Alternative solution encoding method isX1×NM=(x11,x12...x1N,x21,x22...x2N, .......xM1,xM2...xMN), wherexijmeans if fire unit shoots,and iterationT=300.Taking DPSO as compassion method, each algorithm should be operated independently for 30 times.Evaluation criteria include BestVal, avgVal, avgIter and Dx.Relative data on target assignment in WTA problem can be shown in tables.3 and fig.4 as follows.

As the table.3 shows, the optimal value is 11.7798 and at this point, all the passages of 3 fire units respectively shoot 18 targets.Comparatively, IFDPSO2 and IFDPSO3 are of best performance.Although occasionally fail to find optimal value, the results are still in an acceptable range.It is known from table.3 that the results of IFDPSO2 and IFDPSO3 are too close, so the data images of IFDPSO2、DPSO and IFDPSO are just given in this paper.From fig.4, we can see that data fluctuation of IFDPSO is big, and optimal value finding times is less than 17%, so is DPSO.So, this paper converts it to an unconstrained optimization problem.But the distribution of solutions is still decided by constraint setting.Too many constraints and large scale of problem always result in small feasible region and shallow exploration.Under this circumstance, locking feasible region probability of IFDPSO is relatively low, and there are some quick convergences in certain poor positions and poor solutions as a result.Comparatively, IFDPSO2 and IFDPSO3 can conduct global searching in certain range and switch between global searching and local searching.Once local searching is blocked, the algorithm will launch global searching as velocity decays, so, it can avoid local optimal value to some extent.

Relative data about assignment efficiency of fire unit onn=28 batch targets shown in table 4 and fig.5 as follows.

The optical value for the present problem is 4.2546.As table 4 shows, average value gap between IFDPSO and DPSO is not big and both algorithms fail to find the optimal value completely while IFDPSO2 and IFDPSO3 really make it.Moreover, avgIter in table 3 and 4 indicates that the iteration number of IFDPSO2 for two different scales of assignment problems is the least.Based on fig.5, compared with big fluctuation of solution carves in IFDPSO and DPSO, the performance of IFDPSO2 is very stable.Therefor, IFDPSO2 should be the best choice for WTA no matter from the perspective of solution quality or solution effi-ciency.The WTA problem in this paper is just an abstract for target assignment in commanding process, omitting some human factors for the purpose of making algorithm find a result that is approximately close to optimal value.Obviously, IFDPSO2 performance meets the solution requirement.

If we can largely improve weapon system performance or change operating principles,for example, multiple-overlapping of damage zone in operational process, the constraints will be looser.Therefore, theoretically IFDPSO is of better performance on massive attacking targets.

V.CONCLUSIONS

Through analyzing the defects of DPSO, an adjusting parameter for balancing two cognition, velocity mutation and position mutation are designed, and then two sets of improved algorithms and derivations for IFDPSO are put forward, in which the performance of these algorithms has been tested by experiments on solving 0-1 knapsack problem in integer programming.Compared with pseudo-random searching of DPSO in the final stage, it is proved that the serial IFDPSO algorithms are superior to DPSO, and the performance of the serial IFDPSO algorithms is various in solving 0-1 knapsack problem with different settings.On large scale problems, IFDPSO is of the best performance and less influence by knapsack capacity, and IFDPSO1 is comparatively poorer.On medium scale or strict constraint problems, the two derivative algorithms IFDPSO2 and IFDPSO3 perform even better.While on dynamic WTA problem, IFDPSO2 is more likely to find the optimal value with high stability and operating efficiency, which is the best choice for the solution of dynamic WTA problems pr esented in this paper.

ACKNOWLEDGEMENTS

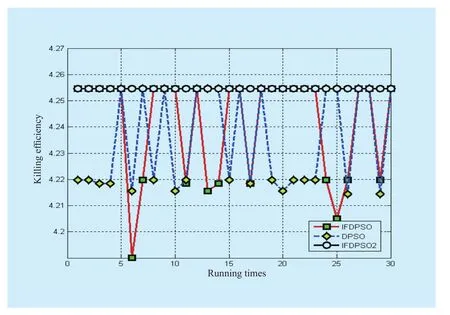
Fig.5 Three DPSO algorithms performance on single fire unit of WTA problem

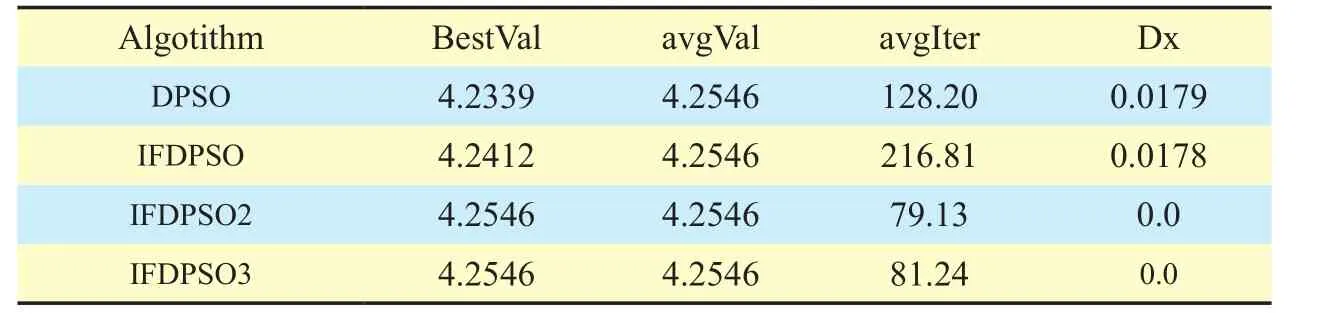
Table IV Four DPSO algorithms performance on single fire unit of WTA problem

The authors would like to thank the referees for their constructive comments as well as helpful suggestions from the Editor-in-Chief which helped in improving this paper significantly.The works described in this paper are supported by The National Natural Science Foundation of China under Grant Nos.61402517, 61573375; The Foundation of State Key Laboratory of Astronautic Dynamics of China under Grant No.2016ADL-DW0302;The Postdoctoral Science Foundation of China under Grant Nos.2013M542331,2015M572778; The Natural Science Foundation of Shaanxi Province of China under Grant No.2013JQ8035; The Aviation Science Foundation of China under Grant No.20151996015.

[1] Lloyd S P.Witsenhausen H S, “Weapon allocation is NP-complete, Proceedings of the Summer Simulation Conference”,Nevada, USA :IEEE, vol.85, no.5, pp 1054-1058, May, 1986.

[2] WANG Lei, NI Ming-Fang, YANG Kuan-Si, WEI Hou-gang, YU Zhan-ke, “Direct Comparison-Improved Combined Chaotic Genetic Algorithm for Solving Weapon-Target Assignment Problem”,Journal of System Simulation, vol.26, no.1,pp 125-131, January, 2014.

[3] GU Jiaojiao, ZHAO Jianjun, YAN Ji, CHEN Xuedong, “Cooperative weapon-target assignment based on multi-objective discrete particle swarm optimization-gravitational search algorithm in air combat”,Journal of Beijing University of Aeronautics and Astronautics, vol.41, no.2,pp 252-258, February, 2015.

[4] XUE Yu, ZHUANG Yi, GU Jing-Jing, CHANG Xiang-Mao, WANG Zhou, “Strategy Selecting Problem of Self-Adaptive Discrete Differential Evolution Algorithm”,Journal of Software,vol.25, no.5, pp 984-996, May, 2014.

[5] Masoud Asadzadeh, Saman Razavi, Bryan A,Tolson, David Fay, “Pre-emption strategies for efficient multi-objective optimization: Application to the development of Lake Superior regulation plan”,Environmental Modelling &Software, vol.54, no.4, pp 128-141, April , 2014.

[6] Kennedy J, Eberhart R C, “A discrete binary version of the particle swarm algorithm, Proc of the World Conf on Systemics”,Cybernetics and Informatics, Piscataway: IEEE Service Center,vol.81, no.4, pp 4104-4109, April, 1997.

[7] Zhang G F, Jiang J G, Xia N, et al, “Solutions of complicated coalition generation based on discrete particle swarm optimization”,Acta Electronica Sinica, vol.41, no.2, pp 323-328, February, 2014.

[8] Xu J Y, Li W L, Wang J J, “Rearch on the divergent analysis and improvement of discrete particle swarm algorithm”,Journal of System Simulation, vol.25, no.15, pp 4676-4681, August,2013.

[9] Guo W Z, Chen G L, “An efficient discrete particle swarm optimization algorithm for multi-criteria minimum spanning tree”,Pattern Recognition and Artificial Intelligence, vol.25, no.4, pp 597-604, April, 2013.

[10] Atanassov K, “Intuitionistic fuzzy sets”,Fuzzy Sets and Systems, vol.20, no.1, pp 87-96, January, 1986.

[11] Fatih Emre Boran, Diyar Akay, “A biparametric similarity measure on intuitionistic fuzzy sets with applications to pattern recognition”,Information Sciences, vol.255, no.5, pp 45-57, May,2014.

[12] Chunqiao Tan, “A multi-criteria interval-valued intuitionistic fuzzy group decision making with Choquet integral-based TOPSIS”,Expert Systemswith Applications, vol.38, no.3, pp 3023-3033,March, 2011.

[13] Ting-Yu Chen, “Bivariate models of optimism and pessimism in multi-criteria decision-making based on intuitionistic fuzzy sets”,Information Sciences, vol.181, no.3, pp 2139-2165, March,2011.

[14] Wang Y Z, Lei Y J, “Adaptive particle swarm optimization algorithm based on intuitionistic fuzzy population entropy”,Journal of Computer Applications, vol.28, no.11, pp 2871-2873, November, 2008.

[15] Wang Y, Lei Y J, “A technique for constructing intuitionistic fuzzy entropy”,Control and Decision, vol.22, no.12, pp 1390-1394, December,2007.

[16] LIN Min, WANG Cheng- Fei, “Dynamic Weapon Target Assignment Method Based on Chaotic Artificial Fish Swarm Algorithm”,Command Control & Simulation, vol.36, no.5, pp 63-67,May, 2014.