土层锚杆蠕变模型研究

陈浩璞+蔡思燕

摘 要：文章以某基坑土层灌浆锚杆为试验对象，由蠕变试验曲线建立三参数的蠕变经验模型，蠕变模型为蠕变位移与荷载水平、时间的组合函数，模拟结果表明位移与荷载、时间的关系函数均采用幂函数是合适的，能为类似土层参数、施工条件下土层锚杆的变形监测及预测提供一定的参考。

关键词：土層锚杆；蠕变模型；蠕变位移

1 概述

随着国内城镇化进程的加速，城市建设往地下空间不断拓展，形成了大量的边坡工程和深基坑工程。锚固技术以其经济有效性被广泛应用于临时支护或永久性加固工程[1]。基坑支护工程中对于锚杆关注最多的是其基本试验和验收试验，蠕变试验做的很少。对于土层锚杆的蠕变，文献[2]进行了土的室内土工试验和土层锚杆的原位测试，表示了土锚蠕变量与锚固荷载及时间的依赖关系，提出了软土层锚杆蠕变收敛的荷载水平上限。文献[3，4]通过对基坑土层灌浆锚杆的拉拔蠕变试验，建立了相应的锚杆拉拔蠕变模型，发现土层锚杆的时间损伤效应比较明显，其长期抗拔力相比瞬时抗拔力有一定的下降。文献[5]研究了粘性土层中常规注浆锚杆的蠕变试验曲线，得到了锚杆拉拔刚度随时间的变化关系，发现锚杆抗拔力随时间增长逐渐降低。总体而言，目前针对土层锚杆蠕变的研究还不够深入，已建立的蠕变模型也只能反映单一荷载水平下的蠕变曲线，对多级荷载水平的蠕变曲线簇适应性不强。因此，本文拟基于某基坑锚杆的拉拔蠕变试验曲线，建立一个能适应各级荷载水平蠕变曲线的蠕变经验模型，以期为土层锚杆的变形预测提供参考。

2 工程背景

2.1 试验方法

某基坑进行了土层灌浆锚杆的蠕变试验[4]。锚杆位于粉质粘土层中，粉质粘土的物理指标如下：重度18.6kN/m3，粘聚力14.4kPa，摩擦角16.9°。锚杆钻孔直径为0.1m，锚杆长7.5m，其中自由段6.0m，锚固段1.5m，锚杆倾角20°。锚杆施工顺序为先钻孔再注浆，锚杆安装完成后最后进行二次注浆，注浆所用材料为水灰比1：1砂浆。

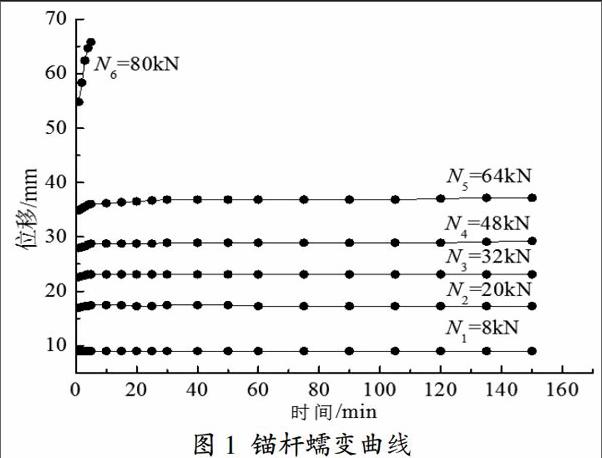
在进行蠕变试验前先进行锚杆的基本试验，得到锚杆的最大破坏荷载Nc=80kN，作为蠕变分级加载的基准。蠕变试验依次按照荷载等级N1（=0.1Nc）、N2（=0.25Nc）、N3（=0.4Nc）、N4（=0.6Nc）、N5（=0.8Nc）、N6（=1.0Nc）逐级加载，每隔一定时间记录一次蠕变位移，每级至少加载150min，若蠕变位移小于0.01mm/min，可加载下一级，否则继续观测，直至破坏为止。

2.2 试验结果

根据Bolzman叠加原理，将试验得到的梯级加载蠕变曲线转化为分别加载下的蠕变曲线，如图1所示。

3 蠕变模型建立

3.1 蠕变模型建立

由图1可知，锚杆蠕变位移既和锚杆拉拔荷载有关，也是时间的函数。根据文献[6-8]，蠕变经验模型中描述位移与时间关系的函数常用的有对数函数、双曲线和幂函数，描述位移与荷载关系的函数常用的有幂函数和双曲线函数。通过试拟合发现，位移与荷载关系函数、位移与时间的关系函数均适合采用幂函数，两者结合即可得到锚杆蠕变位移关于荷载水平以及时间的组合函数表达式：

式中，s为锚杆蠕变位移（mm），Nr，i（=Ni/Nc）为荷载水平，t为每级荷载加载时间（min），a、b、c均为模型待定参数。

3.2 蠕变模型验证

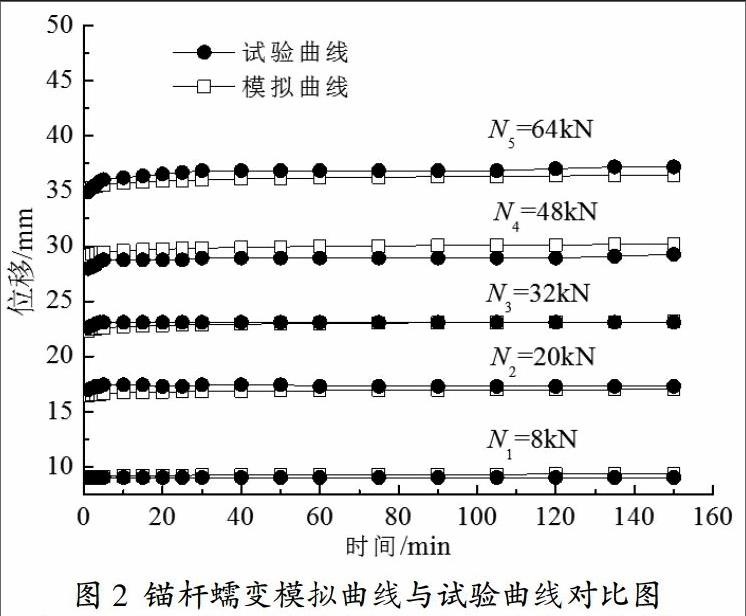
通过最小二乘法回归分析，可以得出本文模型的最优参数a=40.661，b=0.654，c=0.007。根据回归分析得到的参数代入式（1），得到本文建立的模型为

绘出各级荷载水平下的模拟曲线，与试验曲线对比如图2所示。从图中可以看出，每级荷载水平下的蠕变模拟位移与试验实测位移相差均不超过3.5%，模拟曲线与试验曲线非常接近，从而证明本文模型的合理性，说明锚杆蠕变位移与荷载、时间的关系函数均采用幂函数是合适的，能正确描述锚杆蠕变曲线的发展规律，且较准确预测锚杆在各级荷载水平下、各个时刻的蠕变位移，可为类似土层参数、施工条件下土层锚杆的变形监测及预测提供一定的参考。

4 结束语

（1）本文建立的锚杆蠕变经验模型为蠕变位移与荷载、时间的关系函数的组合函数，模拟结果表明位移与荷载、时间的关系函数均采用幂函数是合适的。（2）本文建立的蠕变经验模型只有三个参数，简单实用，能为类似土层参数、施工条件下土层锚杆的变形监测及预测提供一定的参考。

参考文献

[1]程良奎.岩土锚固的现状与发展[J].土木工程学报，2001（03）：7-12+34.

[2]侯学渊，李象范.饱和软地层中土锚的时间效应[J].同济大学学报（自然科学版），1987，15（2）：147-156.

[3]许宏发，卢红标，钱七虎.土层灌浆锚杆的蠕变损伤特性研究[J].岩土工程学报，2002，24（1）：61-63.

[4]许宏发，孙远，陈应才.土层锚杆蠕变试验研究[J].工程勘察，2006（09）：6-8+53.

[5]马永琪.北京地区粘性土中锚杆蠕变特征[J].工程勘察，2014（S1）：731-734.

[6]孙钧.岩土材料流变及其工程应用[M].北京：中国建筑工业出版社，1999.

[7]CC维亚诺夫.土力学的流变学原理[M].杜余培译，北京：科学出版社，1987.

[8]卢萍珍，曾静，盛谦.软黏土蠕变试验及其经验模型研究[J].岩土力学，2008，29（4）：1041-1052.