AGV路径纠偏控制器设计与分析

朱晓祥+陈乃军+殷邦革

摘 要：AGV路径导航算法是提高AGV运行效率的关键问题之一。为了避免AGV在作业过程中受到外界不确定因素影响而偏离既定路径，文章对差速驱动四轮AGV进行了PID控制器设计，能够完成自动纠偏任务。首先，进行AGV运动学建模，分析位置偏差和角度偏差与左、右驱动轮速度差和电机输出电压之间的关系；然后，以位置偏差和角度偏差为输入，以左、右驱动轮速度差为输出，设计PID控制器，对AGV的运动路径进行控制。最后，对PID控制与常规闭环控制进行Matlab仿真对比，验证了PID控制算法的高效性和鲁棒性。

关键词：AGV；运动学；MATLAB；PID控制器

引言

随着科技的进步，AGV（Automated Guided vehicle）作为一种集传感器技术、人机技术和运动控制等技术于一体的综合控制系统，已广泛应用于工农业、物流和军事等诸多领域，成为现今装配生产线、柔性制造和仓储物流智能体系中的关键设备之一。工业AGV作业的环境复杂多样，为快速、准确、安全地完成作业任务，运动控制技术成为AGV路径规划和路径跟踪的关键研究技术[1]。AGV是一类强耦合性、时变的高非线性复杂系统，作业过程中容易受诸多非线性、不确定因素的干扰，精确数学模型的建立相当困难[2]。为了改善AGV控制系统的控制性能，本文运用PID控制的算法，输入变量采用AGV行驶过程中的位置偏差和角度偏差，输出变量采用左、右驱动轮速度差，设计PID控制器，快速、准确地对行驶路径进行纠偏。

1 AGV运动学模型

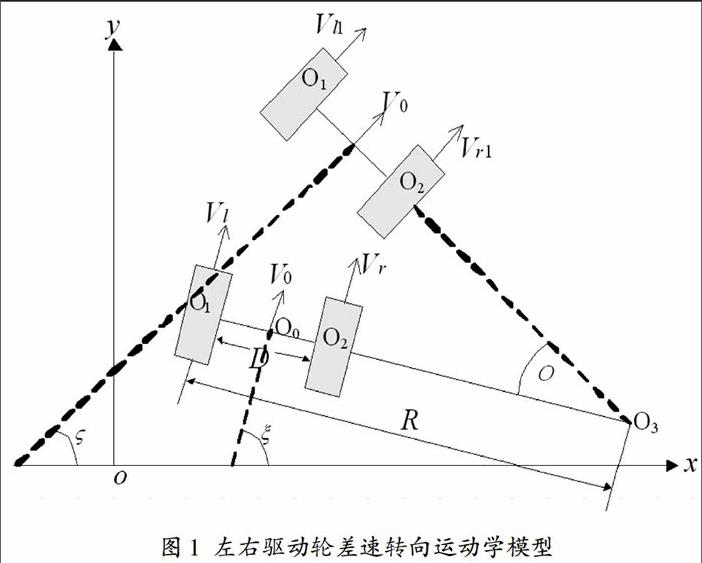
论文的研究对象选用二轮差速转向的四轮AGV。AGV车体的前面两轮为自由轮，后面两轮为独立驱动的驱动轮，由于AGV的运动状态的改变主要是通过调整左右驱动轮的轮速来实现，因此，在不影响运动学分析的情况下，将AGV的的运动模型简化为左右驱动轮的运动[3]。如图1所示。

根据简化模型，建立坐标系。图中xoy为平面坐标系，O1、O2分别为左、右驱动轮的中心和左右驱动轮轴线中心，O3为绕体运动的瞬时圆心。O1O2为两轮的轴间距，其长度为D。Vl、Vr、V0分别为左、右驱动轮和车体中心的速度，车体中心速度大小代表车体的速度，方向代表车体行驶方向。R为车体瞬转向半径。？琢為行驶方向与x轴的之间的夹角。假设w为瞬时角速度。

根据图1所示运动学模型，可知左、右驱动轮速度与角速度w的关系为：

车体运动的速度为：

综上所述：可求得AGV的瞬时角速度w和瞬时转向半径R：

通过改变Vl、Vr的大小关系，可以实现差速驱动AGV的运动方式的改变。

车体经过一小段时间 t，车体中心从O0运动到图1中所示状态。假设车体运动方向上的偏差距离为L，角度偏差为β。 t时刻后，车体运动方向与x轴之间的夹角为γ。

在此运动过程中，由几何分析和机械运动原理可知：

综上所述：车体瞬时转过的圆心角等价于车体运动过程中的角度偏差β。

由此可计算出，AGV在运动过程中的角度偏差和位置偏差与左、右驱动轮速度之间的关系：

AGV在运动过程中， 量一般很小，sinβ≈β，于是得到：

为了精确描述AGV运动过程中，左、右轮驱动速度差与角度偏差和位置偏差的关系，将运动偏差方程与驱动系统的电压和传递函数结合起来，建立系统的动态响应状态方程[4]。

驱动系统中采用两个相同的永磁直流电机，通过Matlab工具箱，将高阶系统转换成低阶系统后，左、右驱动电机的速度、电压和传递函数之间的关系如下：

式中：K和电动机的反电动势有关的常量；U表示电动机的电枢电压；Tm表示电动机的时间常数。

当AGV在行驶过程中，受到外界干扰，偏离预定行驶路径时，控制系统接收到偏差距离反馈的电压信号，改变电动机两端的电枢电压来调整左、右驱动轮转速，纠正AGV的位置偏差和角度偏差。在不改变车体行驶速度的条件下，电压增量和速度增量的数学关系式如示：

由此可知，通过传递函数，可通过改变电压的变化量来控制左、右驱动轮的速度差，实现差速转向和纠偏的目的。电压增量与运行偏差关系如图2所示。

令：x1=？驻V（s），x2=β（s），x3=L（s），则：x=（？驻V，β，L）为状态变量， U作为输入，距离偏差L和角度偏差β作为输出，可得状态方程如下：

通过建立整个控制系统的状态方程，可以看出AGV行驶路径的位置偏差和角度偏差与AGV的行驶轨迹有着复杂的非线性关系。同时，从状态方程中也可明确显示输入电压与角度偏差和位置偏差之间的关系，为控制器的设计提供了理论基础。

2 PID控制器的设计

控制器的输入变量为位置偏差L和角度偏差β [5]。利用PID控制器控制AGV的驱动电机调节左、右驱动轮的速度，实现AGV位置和角度的调整，达到纠偏的目的。位置偏差和角度偏差可由公式（5）和（6）求得。当AGV车体的轴中心点在行驶方向中心的左边时，取L值为负，反之则反；当角度偏差β以顺时钟方向时为负，反之则反。

将选取的永磁直流电机的传递函数简化为二阶系统，得到其传递函数[6]：

在Matlab/Simulink中，建立PID控制器的仿真模型，如3所示。该系统框图由常规闭环控制器和PID控制器两部分组成。

3 仿真结果分析

系统的输入信号为单位阶跃信号，通过仿真，获取仿真曲线，并对比常规闭环控制器和PID控制器与模糊PID控制器的仿真曲线。控制系统误差响应仿真结果如图4示。

4 结束语

通过系统仿真曲线的对比可知，PID控制系统的稳定性比常规闭环控制系统的稳定性更好。在系统中采用PID控制算法，提高了系统的抗干扰能力和减小了振荡幅度。通过计算可知，PID控制器的误差响应的超调量在3%左右，响应时间为0.5s，与常规闭环控制相比，减小了系统的超调量、缩短了系统的响应时间、改善了系统的控制性能。通过MATLAB软件对PID控制算法的动态仿真，验证了PID控制算法的高效性，提高了控制系统的鲁棒性，为AGV运动过程中的纠偏问题提供了一定的理论参考。

参考文献

[1]廖华丽，周祥， 丰，等.基于模糊控制的AGV寻迹算法[J].哈尔滨工业大学学报，2005（7）：896-898.

[2]任柯燕，顾幸生.基于模糊PID对AGV的纠偏控制[J].控制工程，2006（s2）：54-57.

[3]秦闯.基于DSP的AGV控制系统的设计及仿真[D].哈尔滨：哈尔滨工业大学，2014.

[4]刘景柠.AGV路径跟踪控制研究[D].赣州：江西理工大学，2015.

[5]Kova■ic Z， Bogdan S. Fuzzy controller design. Theory and applications[J]. Macromolecular Chemistry & Physics， 2006， 205（17）：23-29.

[6]刘金琨.先进PID控制及其MATLAB仿真[M].电子工业出版社，2003.