基于BP神经网络的区域电离层延迟改正模型研究

董利银

摘 要：电离层研究有着不可忽视的重要性，许多前沿的技术与电离层的研究进展相关。文章对JSCORS实测的电离层数据进行了区域电离层电子含量二阶多项式模型的建立，在结合神经网络技术基础上，建立一个区域电离层电子含量的融合模型。该模型融合了二阶多项式以及神经网络，建模过程中以中误差作为精度评定指标，对两种建模方法进行了横向对比，在0到1点、2到3点，融合模型的拟和中误差相较于二阶多项式精度分别提高了18.1%、22.5%。该工程实例结果表明，神经网络融合模型精度高于二阶多项式模型。

关键词：VTEC；区域电离层延迟；二阶多项式；BP神经网络

1 概述

电离层研究有着重大的意义，许多重要的科学技术都与电离层的研究进展息息相关。由于电离层作用于地球大气层表面，对无线电传播的各项技术都产生了不可估量的影响。更加精确的电离层研究会有效提高卫星导航系统的测速、定位等方面的精度。此外，我国正在建设第二代北斗卫星导航系统，对于电离层延迟的研究对我国的太空发展计划有重要的战略意义。

电离层是距离地球表面约60km至1000km范围内的地球大气，在太阳紫外线、X射线等作用下，大气分子逐渐电离而产生大量自由电子和离子，呈现混沌状态，GPS信号穿过电离层时，其传播速度会发生变化，变化程度主要取决于电子密度和信号频率。对于GPS测量而言，这种延迟误差在天顶方向可达十几米[5]。

目前，为满足各种测量以及定位导航服务。人们根据电离层的各种性质建立了许多的电离层模型，如国际参考电离层模型等。随着空间需求的不断提高、大规模的GPS跟踪网的建立，有必要对电离层模型更加精化。为此，本文利用了中国江苏省CORS基站的数据，通过二次多项式对这些数据进行建模，然后，采用BP神经网络技术来弥补二次多项式的模型偏差产生一种新的修正模型，称为融合模型进行区域电离层延迟改正模型建立。

2 模型构建

2.1 二阶多项式模型

区域电离层的二阶多项式模型在模拟区域VTEC的过程中被广泛应用，是一种精度较高的电离层延迟改正模型。不足之处在于其對数据密集分布有强烈依赖性。对于数据密集和缺乏数据的区域的精度有极大的差别。对于实测数据密集的区域，延迟改正效果非常好。但对于实测数据稀缺的区域却有很大的误差，甚至部分穿刺点的总电子含量会出现负值[5]。

目前国内外电离层研究领域关于该模型的研究分为3参数，6参数，9参数等。根据大量研究表明，9参数模型相较于其他参数选取有着更好的效果和拟合精度。因此，本文将采用9参数模型。

该模型垂直方向的总电子含量预测模型表达式如下：

其中（φ0，λ0）表示测区中心点地理纬度和经度；（φ，λ）表示IPP的纬度和经度；S0是测区中心点在建模时段中间时刻t0的太阳时角，S为IPP在建模时间段的任意观测时刻点t的太阳时角；Eik为待定系数，其中，

（1）式逐项展开形式如下：

将N个测站已知数据代入，得到误差方程组合矩阵形式可以写成：

利用最小二乘法将X9×1的矩阵值求解出来，即VTEC模型的9个系数，其中

然后利用二阶多项式模型的表达式计算已知穿刺点的VTEC值。

2.2 BP神经网络模型及其构建

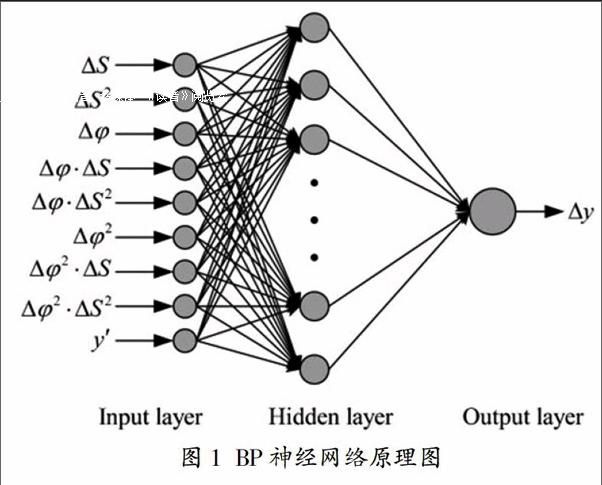
BP神经网络是一种前馈型网络[6]。它集合多个简单处理能力的神经元。通过这些神经元的复合来实现复杂的映射，对于BP算法中隐含层的选择依然是一个有待推敲的问题。由于隐含层数量多有助于增加人工神经网络单元处理能力，但是这样也会让训练过程更加的复杂。一般情况下，隐含层数目是由少到多实验的过程。本文的神经网络模型结构如图1。其中有9个输入层，1个输出层，此外还有多个隐含层节点[4]。对于输入的讯息，首先从输入层传播到隐藏层，经过激活函数将隐含层的数据传输到输出节点。

该模型将以每组数据的八项特征值为输入层， 以VTEC真值为输出层进行模拟，从而建立模型。本文的神经网络模型有8个输入层，1个输出层，此外还有23个隐含层。本文选取的学习速率是1.5h，平滑因子参数为0.7，分级迭代级数为14，训练控制误差为0.3。如上的训练过程结束后，我们将得到指定区域内预测模型。预测值与真值作差即可得残差以及中误差。

计算多项式模型的拟合偏差值，将已知参数带入表达式中，可得到已知点的二阶多项式的模型预测值。此时，二阶多项式预测模型相对真值的拟合偏差值的计算公式为：

2.3 建立基于BP神经网络的融合模型

根据前文二阶多项式的部分，我们得到了一个偏差较大的二阶多项式预测模型并计算出该模型相对于真值的拟合偏差。我们将该偏差值作为输出层进行神经网络训练，以期得到模型偏差值的预测值，进而改正二阶多项式模型形成全新的BP融合模型。利用式（7）即算得建立的神经网络及二阶多项式融合模型（BP-DPM模型）的VTEC预测值VTECpred。

该模型将以每组数据的九项特征值（包括二阶多项式的拟合值）为输入层，以VTEC二阶多项式拟合偏差为输出层进行模拟，从而建立模型。相对于人工神经网络模型来说，该模型加入了一个输入层，即为每个穿刺点处的二阶多项式拟合值[4]。

2.4 模型精度评定

我们在利用以上几种方式对区域电离层的总电子含量预测进行建模时，还有一个最重要的问题就是要将每种模型的建模精度进行计算，以保证我们的建模工作成果可靠。

如上介绍了三种电离层预测模型的建模过程和计算公式。利用我们已经提取得到的电离层电子含量VTEC真值，可以计算出各个模型的中误差。本文用中误差来表征模型的计算精度。式（8）即为建模的精度表征：

其中，i为检验样本，n为样本个数。

3 工程实例

本文所提及的建模数据均采用JSCORS于2010年11月19日0：00～4：00的数据（其中包含了穿刺点（IPP）编号，测站位置，IPP经度，IPP纬度，观测时间，VTEC真值），将其分为建模数据和模型数据检验组。这些测站均匀分布于北纬30°至35°、东经116°至123°区域范围内，共68个测站。这些数据中的电离层穿刺点VTEC真值的获取方法为双频GPS观测值或根据CORS观测数据利用相位平滑伪距方法从CORS数据中提取出。将其分为建模数据组和检验数据组，选取其中的3个测站数据组进行建模，另外33个测站数据进行检验。

在此工程实例中，我们选取0到1时、2到3时共3200组数据，按照上文叙述的方法先利用最小二乘法求出二次多项式模型的其他八个参数，代入得到二次多项式的模型值。接着进行中误差计算，得到模型数据和检验数据的中误差。利用所得到的二次多项式和真值的残差继续进行神经网络融合模型的建立，最后进行0到1时和2到3时的建模结果中误差比较。

如图2是0到1时二项式模型和融合模型中误差的比较，明显看出几乎所有测站的融合模型的VTEC中误差均小于多项式模型的。图3是2到3时的模型中误差比较，同样可以明显的看出几乎所有测站的融合模型的VTEC中误差均小于多项式模型的，并且融合模型的中误差曲线相较于多项式模型更加平稳，最大中误差值峰值低于二阶多项式，更好的预测电离层电子总含量。

将所有测站的模型中误差置于表1中比较，可以对比得到在0到1点、2到3点，神经网络融合模型的拟合中误差相较于二阶多项式精度分别提高了18.1%、22.5%。

4 结束语

在文中，我们建立了一个9参数的二阶多项式电离层延迟改正模型并计算出其拟合残差以及中误差。建立了一个神经网络电离层延迟改正模型并计算出其中误差。利用二阶项电离层延迟改正模型的计算残差建立并评估了一个二阶多项式以及神经网络的融合模型。

综合两个时段的结果，神经网络融合模型的拟合精度相较于二阶多项式模型分别提高18.1%和22.5%。通过中误差对比，神经网络融合模型更加平稳，总体中误差值更低，预测效果更佳。

通过对数据结果以及建模過程进行分析，不难得出如下结论：

（1）在中国的江苏省区域神经网络与二阶项的融合模型精度高于单独的二阶多项式模型。

（2）在中国江苏省区域内，所研究的二阶多项式改正模型有着更大的中误差，而融合模型模拟效果更加稳定，曲线更加平稳，精度更高。

参考文献

[1]胡伍生，高成发.GPS测量原理及其应用[M].北京：人民交通出版社，2002：1-13，58-75，91-102.

[2]袁运斌，霍星亮，欧吉坤.精确求定GPS信号的电离层延迟的模型与方法研究[J].自然科学进展，2006，16（1）：40-48.

[3]胡伍生.神经网络理论及其工程应用[M].北京：测绘出版社，2006：1-134.

[4]W.S.Hu，D.Y.Zheng，W.F.Nie.Research on methods of regional ionospheric delay correction based on neural network technology.Survey Review，2014（46）：167-174.

[5]吴宇航，陈秀万，等.电离层延迟改正方法评述[J].全球卫星定位系统，2008（33）.

[6]Yunbin Y， Xingliang H， Jikun O. Models and methods for precise determination of ionospheric delay using GPS. Progress in Natural Science，2007，17（2）：187-196.