等效均匀化方法在基于棒尺度的精细功率计算上的应用

刘琨+陈长+王杰+田超+陈定勇

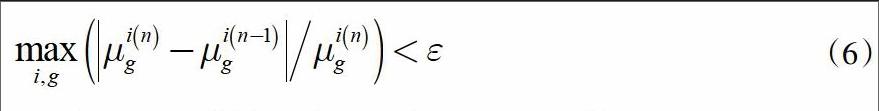
摘 要：在堆芯计算过程中，通过采用基于棒尺度的中子扩散方程求解，可以充分考虑燃料组件内的局部非均匀性对于栅元中子注量率的分布影响，获得基于燃料棒的精细少群中子注量率分布，从而提高燃料栅元的微观反应率计算精度。相应地，在均匀化参数计算过程中采用等效均匀化方法（SPH），用以保证在“组件输运-堆芯扩散”过程中基于棒尺度的计算网格上的中子反应率守恒。研究表明：等效均匀化方法提高了堆芯扩散计算过程中棒功率的计算精度。

关键词：反应堆；中子擴散方程；等效均匀化方法

1 概述

在堆芯计算中，中子学方法要求在堆芯物理求解过程中充分考虑组件内存在的局部非均匀性对于燃料棒栅元的中子注量率分布的影响，获得基于棒尺度的精细少群中子注量率分布，从而提高燃料棒栅元的各种围观反应率的计算精度。而传统压水堆燃料管理计算中，堆芯物理采用基于节块方法的中子扩散求解器进行燃料管理计算和核设计计算分析（如SIMULATE-3[1]，SMART[2]等），在获得堆芯各节块的中子注量率等物理计算结果的基础上，采用功率重构方法，获得堆芯内燃料棒的精细功率分布结果。使用节块方法进行堆芯计算时，生成组件少群参数的过程中已经将组件均化处理为节块计算所需的信息（节块少群宏观截面及不连续因子等），组件内的非均匀特性被均匀化处理，实际上无法得到组件内各栅元真实的通量分布。通过节块方法和精细功率重构的方法和真实堆芯内栅元均匀化方法进行功率计算求解是存在着差异的。需要针对核反应系统开展栅元均匀化的通量求解。

为了实现堆芯层面的栅元均匀化计算需求，同时满足堆芯中子注量率计算效率，本文采用SRAC程序[3]进行二维组件的共振计算和输运计算，获得组件少群均匀化参数；采用CITATION程序[4]进行三维堆芯的扩散计算，以获得堆芯内各栅元网格内的中子注量率分布。本文采用SPH等效均匀化方法[5]，进行少群截面的修正。通过引入能群相关的SPH（Super homogenization）因子，进而实现对少群截面参数调整，保证均匀化前后反应率守恒。

2 等效均匀化方法实现

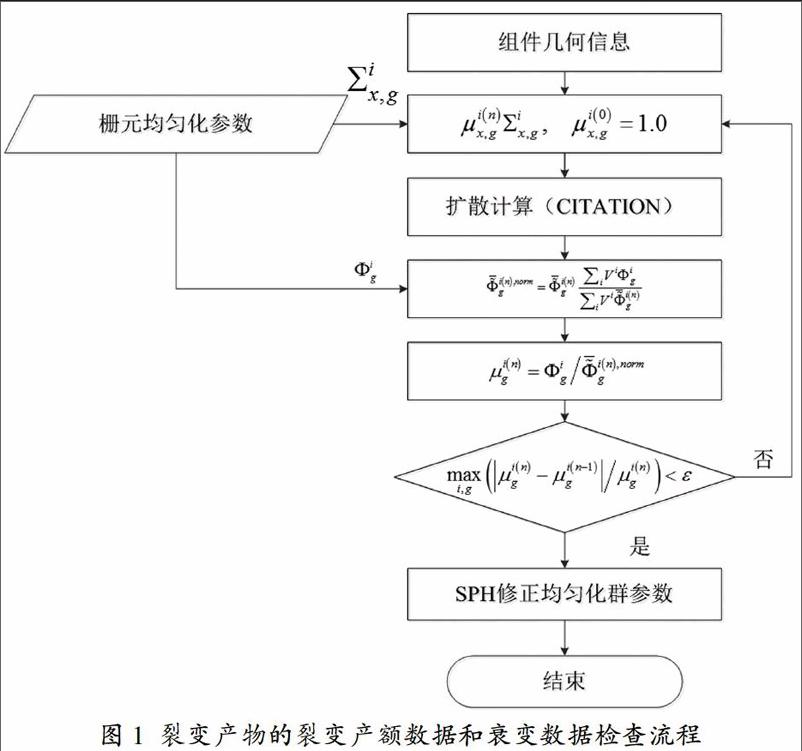
组件输运程序（SRAC）和堆芯扩散程序（CITATION）计算SPH的计算流程。在SPH迭代过程中，输运计算所获得组件均匀化参数如式（1）所示：

采用SPH修正后的中子学参数进行扩散计算，如式（2）所示。

式中，i-空间均匀化区域标识，g-能群标识。

最终获得各区域的各中子能群的平均中子注量率（式（3）），并保证总的中子注量率积分守恒进行反应率归一，如式（4）所示。式下次迭代所需的能群相关的SPH因子计算结果

其中，？滋■■=1.0，迭代收敛准则ε（10-4）用于判断SPH因子迭代收敛，如式（6）所示。

图1给出了参数均匀化过程中，SPH因子的计算流程。

3 数值验证

OECD-L336 C5基准题由L.C. Lefebvre 等人定义，该问题描述了一个1/4对称的堆芯，其中UOX和MOX燃料组件棋盘式布置方式。采用该基准题进行程序进行SPH计算模块的验证。均匀化栅元栅距为1.26cm，组件采用17×17压水堆组件排布方式，外部慢化剂反射层厚度为21.42cm，堆芯外围为真空边界条件。

表1给出了CITATION和DORT[8]进行栅元均匀化求解后堆芯keff结果比较。棒相对功率偏差结果则如表2所示。当前计算结果表明：在进行堆芯反应性计算时，CITATION和DORT的计算结果吻合较好；棒的相对功率偏差的均方根结果显示主要的棒功率偏差出现在组件-组件或组件-反射层的交界面附近，这是由于中子注量率梯度变化较大导致的。针对堆芯扩散求解方法计算时采用的少群参数进行SPH因子修正，用以保证组件输运计算到堆芯扩散计算过程中的中子注量率守恒。

4 应用分析

基于现役压水堆燃料组件几何和材料定义，进行了单组件的建模计算，分析了等效均匀修正对于棒尺度的精细功率计算结果的影响，比较了等效均匀修正对于。通过SRAC程序产生SPH修正的均匀化两群群常数，使用CITATION进行相应的堆芯扩散求解。当前选取组件内具有较强非均匀性的算例（控制棒插入和带有20根钆棒装载方式），进行了相应的反应性计算分析。组件示意图如图 2所示。

表3给出了等效均匀化对于计算算例的无限增殖因子（kinf）的结果。结果表明：由于控制棒的插入或是可燃毒物钆棒的装载，组件内非均匀性较强，因此在进行基于棒尺度的精细功率计算时，通过采用SPH修正因子，保证组件输运计算和堆芯扩散计算的反应率守恒，保证了中子学计算的精度。

5 结束语

在基于栅元均匀化的全堆棒尺度的中子扩散方程求解中，通过SPH等效均匀化因子进行中子反应截面的修正，进而保证在“组件输运-堆芯扩散”计算过程中的中子反应率守恒，从而保证了基于棒尺度的精细功率计算的准确性。OECD-L336基准题验证了当前的SPH修正计算流程的正确性。通过现役压水堆燃料组件的棒尺度精细功率建模计算结果表明，采用SPH等效均匀化因子，针对于具有较强的非均匀问题，可以有效的保证中子学计算的准确性。

参考文献

[1]DiGiovine AS， Rhodes JD. SIMULATE-3： Advanced Three-Dimensional Two-Group Reactor Analysis Code. User' Manual[R]. Studsvik Scandpower， 2005.

[2]Greg HH， Richard CA. Nodal Code Developments at FRAMATOME/BWFC[C]. Proceedings of Topical Meeting on Advances in Reactor Physics， Knoxville， Tennessee， USA， 1994.

[3]Okumura K， Kugo T， Kaneko K， et al. SRAC2006： A Comprehensive Neutronics Calculation Code System[R]. Japan Atomic Energy Agency， 2007.

[4]Fowler TB， Vondy D， Cummingham GW. Nuclear Reactor Analysis Code： CITAITION[R]. Oak Ridge National Laboratory， 1969.

[5]Hebert A. A Consistent Technique for the Pin-by-Pin Homogenization of a Pressurized Water Reactor Assembly[J]. Nuclear Science and Engineering， 1993， 113 （3）： 227-238.

[6]Grundmann U， Mittag S. Super-Homogenisation Factors in Pinwise Calculations by the Reactor Dynamics Code DYN3D[J]. Annals of Nuclear Energy， 2011， 38 （10）： 2111-2119.

[7]Lefebvre LC， Mondot J， West JP. Nuclear Energy Agency. Benchmark Calculations of Power Distribution within Assemblies[R]. 1991.