前端带小电容整流器的感应电机变频驱动控制

(1.湖南电气职业技术学院,湘潭411101;2.湖南工程学院 湘潭411101)

0 引 言

感应电机由于具有技术成熟、可靠性高、成本低、维护性好等优点,在变频驱动应用中得到了广泛使用[1-3]。而在低成本三相感应电机(以下简称IM)变频驱动应用中,例如空调系统和小功率变频器,通常采用二极管整流器作为前端直流源,因为不控整流器成本较低,可靠性高[4-6]。如图1所示,在这类传动系统中,直流侧通常使用较大电解电容器来平衡瞬时输入和输出功率差异,以及抑制电压尖峰[7-8]。但直流侧电解电容的使用将会显著增加系统体积重量,同时由于电容自身可靠性不高,加上其寄生电感可能导致的电压尖峰,将导致系统可靠性进一步降低。

图1 前端带二极管整流桥的感应电机驱动系统

为了提高系统可靠性,越来越多的文献报道了对电解电容器运行监控的研究[9-11]。其中离线监测技术由于需要额外的测量和电容模型的相关参数,导致了监测的复杂度,因此不利于工程实践[12]。而文献[13]提出的实时在线监测技术不能应用到如图1所示的主电路拓扑结构中。另一方面,也有越来越多的文献开展了对变频器控制技术的研究,以期尽量减少直流母线电容的容值,但这些研究绝大部分是基于前端为三相可控整流供电或单相整流桥供电的变频器,不适用于图1的系统[14-17]。而且这些研究方案都采用了传统的闭环电流解耦控制来调节电机的转矩和磁链,若直流电容进一步减小将仍然导致变频器输出功率波动。因此文献[18]加强了电流控制的复杂度来应对,综合应用了弱磁控制、抗饱和控制和过调制控制等方法,但这将导致控制器动态性能的减弱。

本文在前述文献研究基础上,设计了一种带小电容不控整流器供电IM变频驱动系统的新型复合控制方案。控制方案在磁场定向电机模型控制模式(以下简称FOMMC)的基础上实现了与六角形电压矢量边界控制模式(以下简称HVVMC)的结合和灵活切换,同时综合运用了转速估计算法,故也是一种无速度传感器方案。其中在FOMMC控制模式下,控制器根据转矩指令和转子磁链指令生成输出电压参考,而在直流电压较低时,则采用HVVMC模式以实现最大电压利用率。最后通过1.5 kW的IM驱动控制平台,结合使用20 μF薄膜电容器对控制策略的有效性进行了试验验证。

1 新型IM驱动控制器设计

1.1 IM动态数学模型

IM的定子电压和磁链动态方程可以表示为如下的矢量形式[19]:

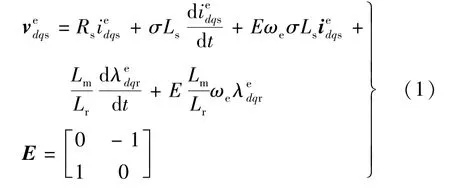
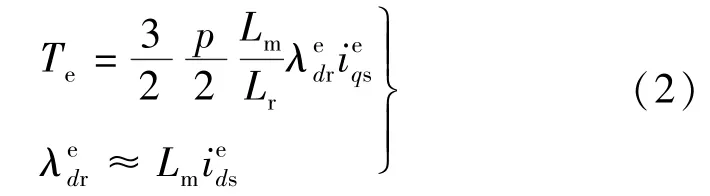
式中:p为极对数,式(1)中定子电压方程可写成:

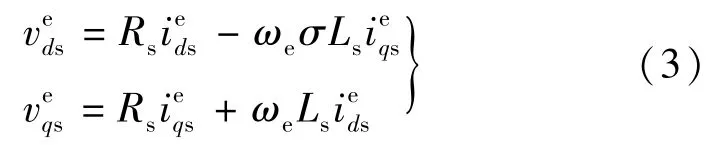
1.2 新型控制器模式切换结构

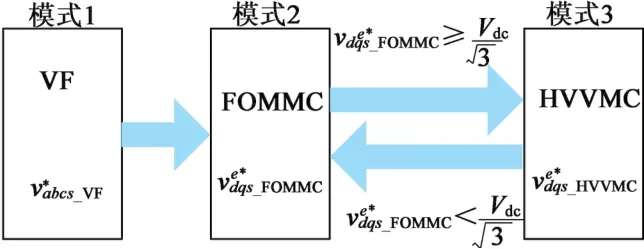
图2 新型控制器模式切换结构

1.3 新型控制器原理分析

图3为d-q旋转坐标系下式(4)和式(5)的图形化描述,图中还绘出了电压矢量六边形边界,其中垂直于d轴的实线为电磁转矩指令,平行于d轴的虚线为转子磁链指令。当电压参考在电压矢量六边形边界以内时,根据模式切换原理,将工作在FOMMC模式,基于单机模型可得输出定子电压指令:

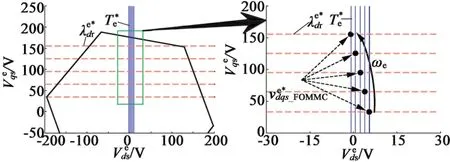
图3 FOMMC模式下的电压矢量选择

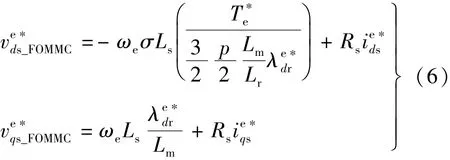
从图3中还可以看出,直流电压下降将导致电压矢量六边形边界缩小,或转速持续上升都可能使旦超过边界,控制器将转为HVVMC模式。在HVVMC模式下,控制器将根据最大直流电压尽可能生成所需要的电磁转矩,同时调节磁链使得在电机工作在弱磁区域。在实际IM驱动中,FOMMC模式一般在转速较低时应用,而HVVMC模式一般在转速较高时使用,基于此,假设HVVMC模式下的定子电阻压降可以忽略,该假设将不影响电机的控制性能。故在HVVMC模式下的定子电压方程可以简化:

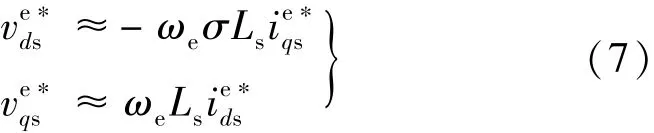
结合式(2)的第一式和式(7),可以得到转矩指令和d,q轴电压之间的关系:

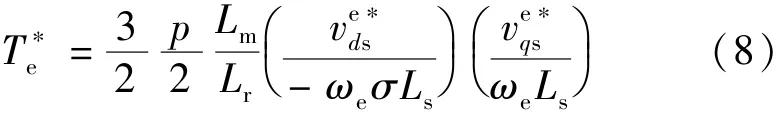
其中转矩指令的轨迹在d-q轴电压平面将构成双曲线。在图4中,转矩曲线与旋转电压矢量六边形之间的交点即为在HVVMC模式下的输出电压矢量,而矢量六边形的边界取决于直流母线电压的大小。每个旋转电压矢量六边形的边界具体可以描述为如下形式[18]:

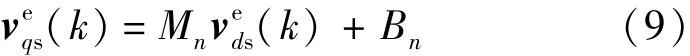
式中:Mn和Bn是由每个给定六边形边界所确定的常量。

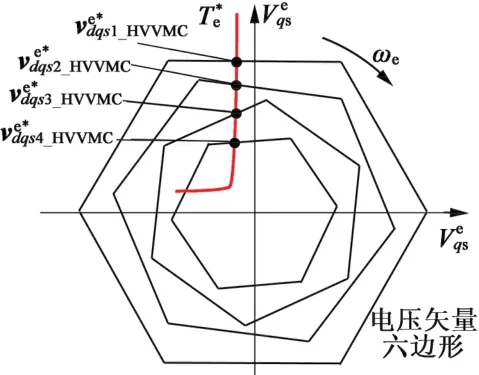
图4 HVVMC模式下的电压矢量选择

在图4中还可以看出,式(9)对应的六边形边界和电磁转矩曲线有两个交点,也就是说在HVVMC模式下可提供两个定子电压指产生所需的转矩,具体如图5所示。但是,考虑到vHVVMC是唯一能满足所需定子磁链的电压矢量,所以选择其作为真正的输出,具体的表达式如下:

式(10)所描述的算法可以在直流母线电压波动时迅速对电压矢量求解以获取需要的电磁转矩。

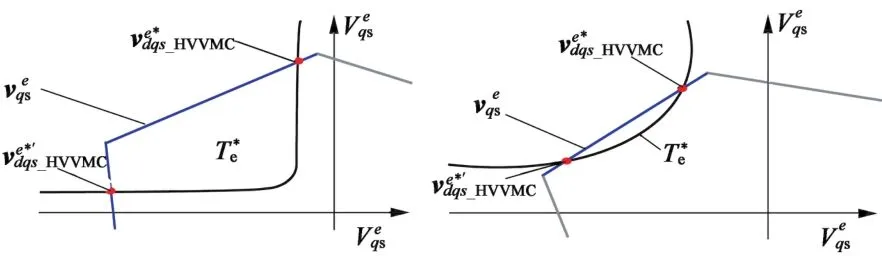
图5 电压矢量可行解选择

进一步可以对HVVMC算法下如何使得电机运行在弱磁工作区进行分析。如图5所示,一个给定的转矩指令轨迹将和旋转电压矢量六边形进行交叉,交叉点即电压指令,当直流电压下降时,交叉点也随着q轴向下移,有较低的q轴电压分量。从式(7)可以看到,较低q轴电压分量意味着降低d轴电流,从而将减小在给定转子速度下的磁链。这也意味着自动弱磁和最大电压利用率可以同时实现,而不需要增加一个额外的控制。

此外,FOMMC模式和HVVMC模式之间的快速平滑切换是可行的,也不需要额外的控制,因为电机FOMMC模式下电磁转矩控制中不包含积分项,这是和传统转矩电流闭环控制是不同的。模式的平滑切换将对变频器使用小电容非常有利,因为可以应对频繁的直流电压波动。

1.4 参数扰动补偿

考虑到磁饱和和测量计算误差将导致式(6)的第一式、第二式,式(10)的第一式、第二式中的电机参数发生扰动,进而使转子磁链在FOMMC和HVVMC模式下波动,同时上述这些公式计算得到电压若存在偏差,则进一步导致不正确的定子电流,从而加大电机运行损耗。图6为测量得到的当电机参数Ls,Rs和σLs存在偏差时定子电流的变化曲线,测量时的转速保持在60%额定速度和70%额定转矩,具体试验用的电机主要参数如表1所示。

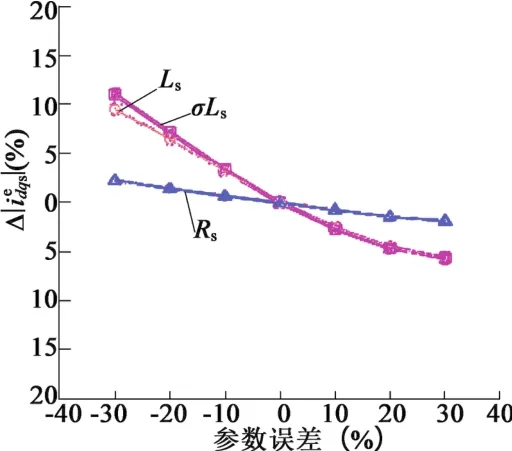
图6 电机参数扰动导致的电流偏差

表1 试验用IM主要参数

考虑到工程实践中采用对电机参数扰动的在线补偿是实现较好电机控制性能的有效方案,因此本文采用了一种电压扰动状态滤波器设计。图7为状态滤波器的控制框图。从图7中可看出采用了一个PI型龙伯格电流观测器来估计参数变化导致的电压扰动。因为电压指令v前馈给电压扰动观测器,所以可在其输出得到电压扰动值Δqs_D。由于 HVVMC模式下电压指令位于电压矢量六边形边界上,所以定子电流含有6倍频谐波,因此引入了谐振滤波器。

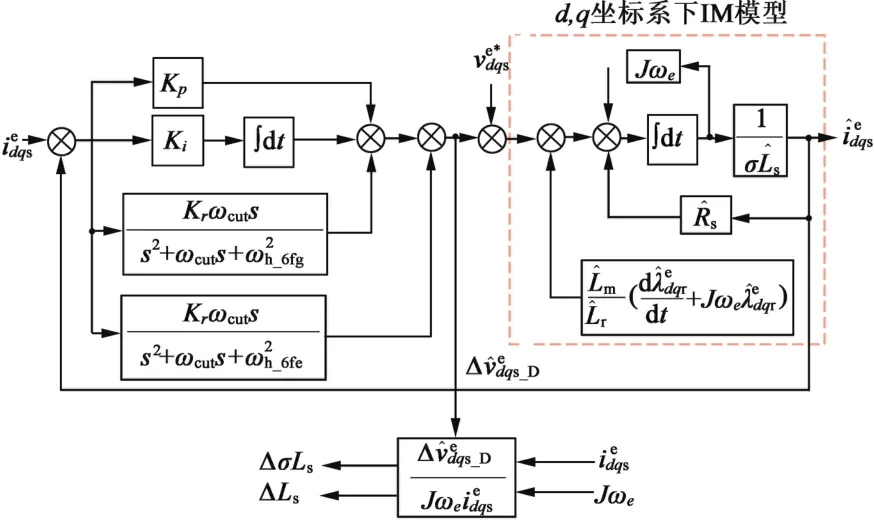
图7 状态滤波器设计

通过对图7中的状态滤波器结构推导可以得到s域下的方程如下:

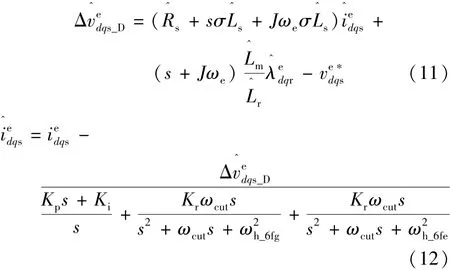
式中:Kp和Ki为PI调节器的比例和积分参数,Kr为谐振增益;而ωh_6fg,ωh_6fe和ωcut分别为6倍频电网频率、6倍频同步频率和截止频率;上标“^”代表了变量的估计值。将式(12)代入式(11)可以得到:

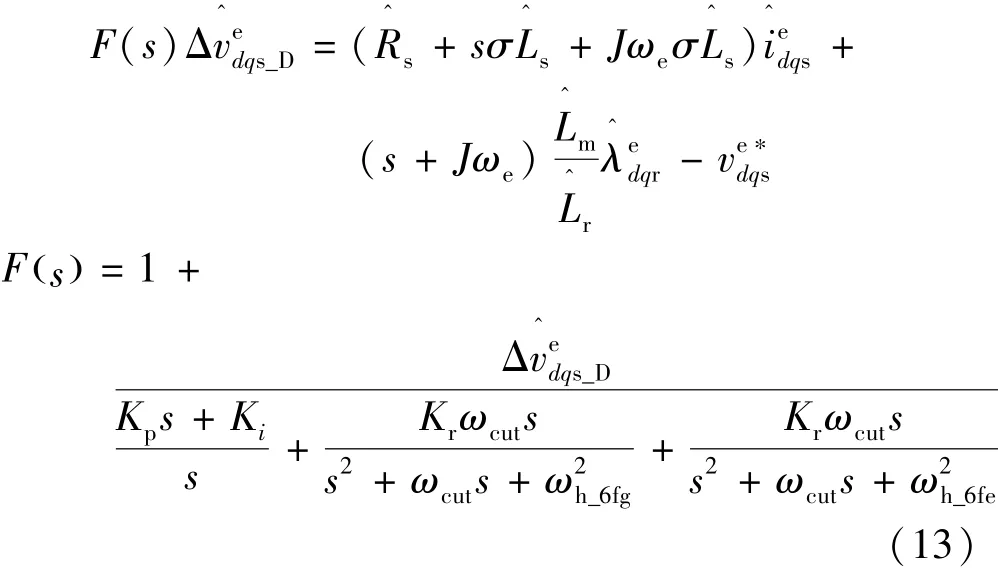
根据终值定律,稳态时即s→0,进而d,q轴电压扰动可以通过将式(1)代入式(13)得到:

式中:ΔRs=-Rs;ΔσLs=-σLs。 基于转子磁场定向原理,式(14)可简化:

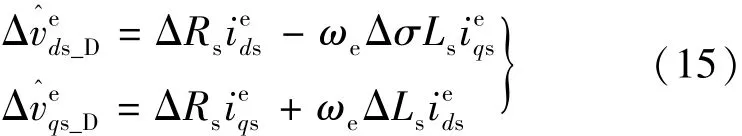
式中:ΔLs=-Ls。从式(15)可以看出,将定子电阻导致的压降忽略,则有:

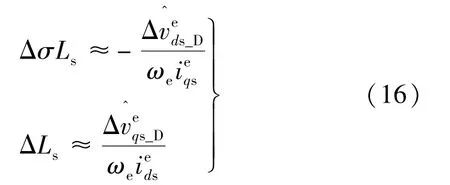
图8为在60%额定速度和70%额定转矩时对参数扰动的补偿仿真结果。图中ΔLs被模拟具有+15%的偏差,在t=1 s后进行了参数补偿,约1 s后转子磁链偏差修正降低至零。仿真结果显示通过参数扰动补偿,可以在参数不匹配的情况下也可得到定子电流和转子磁链的精确控制。

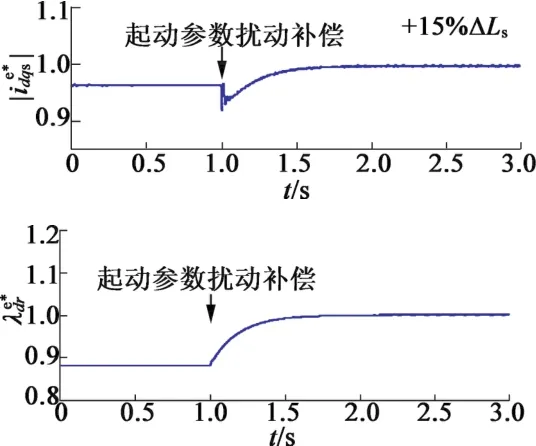
图8 参数扰动补偿仿真结果

1.5 新型驱动控制器框图

图9为新型IM驱动控制的整体框图,它采用了文献[21]中所涉及的转子位置观测器,故也是一种无速度传感器控制方案。从框图中可以看出,变频器的参考电压矢量有3个输入途径,首先是电机起动过程采用的VF模块可以输出参考电压,但起动结束后则将其屏蔽;然后是FOMMC模块开始运行,接收到转速PI外环的输出后通过运算得到电压参考;当直流电压降低导致FOMMC模块生成的电压参考超过限制值时,则自动切换到HVVMC模块,该模块在转速PI外环输出的转矩指令基础上综合使用状态滤波器实现参考电压的输出。得到参考电压指令后,PWM模块将生成控制脉冲实现电机驱动控制执行。

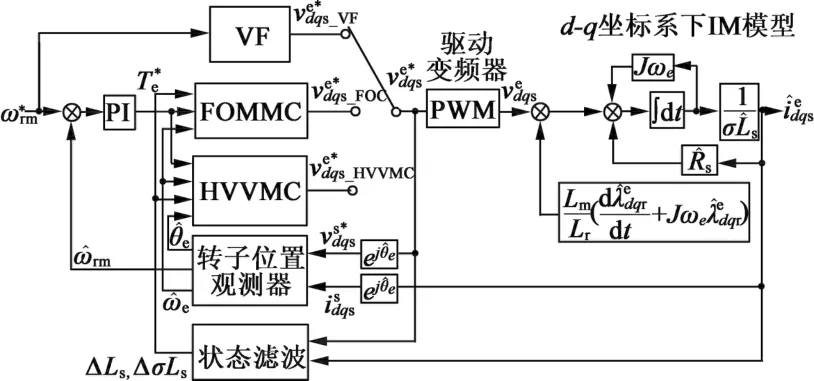
图9 新型控制策略整体框图

2 试验验证

用1.5 kW感应电机和带20 μF薄膜电容的不控整流桥搭建了试验系统以验证前述控制策略的有效性,其中采用了一个与感应电机功率相同的直流电机对负载进行模拟,核心控制算法采用TI公司的28335芯片实现,变频器主电路采用三菱公司的IPM模块构建,IM的参数如表1所示,其他主要试验系统参数如表2所示。

表1 试验系统主要参数

图10为新型控制策略作用下电机在额定转矩时的稳态运行试验波形,此时转速为额定值的90%。从图10(a)中可以看出,由于直流侧电容容值降低,直流电压出现了6倍频电网频率的波动;而图10(b)所示,控制模式在FOMMC和HVVMC之间实现了平滑快速地切换,其中高电平为HVVMC模式,其出现的时间对应图10(a)中直流电压的低位;从图10(c)和图10(d)所示的电磁转矩和转子磁链波形可以看出,虽然存在控制模式切换,但输出电磁转矩平稳,磁链也波动较小;而从图10(e)的电压指令d-q坐标系图可以看出,电压指令的轨迹接近于最大六边形边界,因而实现了在直流电压下降时的最大电压利用。

图10 新型IM驱动控制器试验结果图

图11为电机在额定转速下负载转矩变化时的试验波形。从图11(a)中可以看出,由于模式切换是平滑而迅速的,故尽管负载转矩发生多次突变,转速仍较稳定地保持在1 500 r/min;而图11(b)中可以从转矩电流的变化看出转矩的变化,其中包含了从25%额定转矩到50%额定转矩,再到100%额定转矩的过程。试验结果说明在全负载范围内控制器都可以实现较好的控制性能,因而系统可靠性和生命周期的提高是不以牺牲控制性能为代价的。

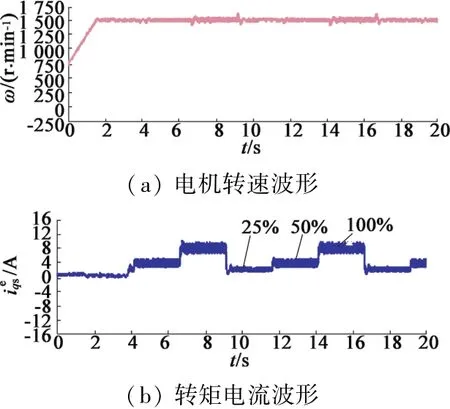
图11 负载转矩变化时的试验结果

3 结 语

为了降低前端由不控整流器供电的IM变频驱动系统中直流侧电容的容值,本文设计了新型复合模式切换型控制器,其结合了FOMMC模式控制和

HVVMC模式控制,并实现了平滑切换,同时设计了参数扰动补偿状态滤波器,最后经过试验研究,可总结如下结论:(1)新型驱动控制策略在直流电压波动时能实现平滑地在FOMMC模式和HVVMC模式之间切换,保证了最大直流电压利用率。(2)控制器中增加的状态滤波器能够较好地解决电机参数扰动问题,试验结果显示在新型控制策略作用下,直流侧容值减小,而变频器的可靠性提高,同时还保持了较好的电机控制性能。

[1] 张兴华,孙振兴,王德明.电动汽车用感应电机直接转矩控制系统的效率最优控制[J].电工技术学报,2013,28(4):255-260.

[2] 梅从立,黄文涛,殷开婷,等.基于Hammerstein模型的感应电机变频器调速系统神经网络控制[J].控制与决策,2015,30(6):1148-1152.

[3] 赵海森,王博,王义龙,等.势能负载条件下感应电机变频-调压分段节能控制策略研究[J].中国电机工程学报,2015,35(6):1490-1497.

[4] 姜卫东,李王敏,佘阳阳,等.四象限电机控制器直流侧PWM整流器变系数控制策略[J].微特电机,2014,42(2):63-66.

[5] 胡杨,褚齐超,佘阳阳,等.以单相PWM整流器为前端的永磁同步电动机背靠背驱动系统[J].微特电机,2014,42(6):35-39.

[6] 张钢,柴建云.一种电机驱动用大功率网侧变流系统研究[J].电力电子技术,2014,46(1):93-95.

[7] LEE W F,KIM M,YOON J,et al.Condition monitoring of DC-link electrolytic capacitors in adjustable-speed drives[J].IEEE Transactions on Industry Applications,2008,44(5):1606-1613.

[8] GADPERI M L.Life prediction modeling of bus capacitors in AC variable frequency drives[J].IEEE Transactions on Industry Applications,2005,41(6):1430-1435.

[9] 潘志文,崔桂梅.电力电容器的电容值测量及失效分析[J].物理测试,2011,29(6):59-62.

[10] 李享,李岱霖,叶雪荣,等.LED开关电源中铝电解电容性能退化模型的研究[J].电源学报,2012,10(6):51-64.

[11] LAYHANI A,VENET P,GRELLETt G,et al.Failure prediction of electrolytic capacitors during operation of a switchmode power supply[J].IEEE Transactions on Power Electronics,1998,13(6):1199-1207.

[12] IMAM A M,HABETLER T G,HARLEY R G,et al.Real-time condition monitoring of the electrolytic capacitors for power electronics applications[C]//IEEE International Conference on Applied Power Electronics.IEEE,2007:1057-1061.

[13] LEE D C,LEE K J,SEOK J K,et al.Online capacitance estimation of DC-link electrolytic capacitors for three-phase AC/DC/AC PWM converters using recursive least squares method[J].IEE Proceedings-Electric Power Applications,2005,152(6):1503-1508.

[14] INAZUMA K,URSUGI H,OHISHI K,et al.High-power-factor Single-phase Diode Rectifier Driven by Repetitively Controlled IPM Motor[J].IEEE Transactions on Industry Electronics,2013,60(10):4427-4437.

[15] LEE W J,SON Y,HA J I.Single-phase active power filtering method using diode-rectifier-fed motor drive[C]//IEEE Energy Conversion Congress and Exposition.IEEE,2013:2461-2465.

[16] 邱涛,陈林康.变频器中PWM整流器的设计及仿真[J].微特电机,2006,34(5):17-19.

[17] 尹璐,赵争鸣,鲁挺,等.基于双DSP的双PWM变频器控制平台设计[J].电力自动化设备,2013,33(11):148-153.

[18] CHOI C H,SEOK J K,LORENZ R D.Wide-speed direct torque and flux control for interior PM synchronous motors operating at voltage and current limits[J].IEEE Transactions on Industry Applications,2013,49(1):109-117.

[19] 刘新正,苏少平,高琳.电机学[M].北京:电子工业出版社,2014.

[20] 周志刚.一种感应电机的解耦控制方法[J].中国电机工程学报,2003,23(2):121-125.

[21] 史婷娜,肖竹欣,肖有文,等.基于改进型滑模观测器的无刷直流电机无位置传感器控制[J].中国电机工程学报,2015,35(8):2043-2051.