用建模突破磁偏转教学难点

倪富昌

摘 要： 带电粒子在匀强磁场中做匀速圆周运动，进出磁场所涉及的几何关系众多。如果建立几个相关的几何模型，不仅方便学生记忆，而且还加深了学生对洛伦兹力的理解和应用，会有效地突破磁偏转这一教学难点。

关键词：磁偏转；建模；几何关系

中图分类号：G633.7 文献标识码：A 文章编号：1003-6148（2017）4-0050-2

带电粒子垂直进入匀强磁场，在磁场中做匀速圆周运动。粒子进出磁场的几何关系众多，面对各种几何关系，如何找圆心求半径呢？对此，有的从边界入手，有的从问题出发，有的抓住临界等等。对于繁多的处理方法，学生学习后仍感到繁杂。学完之后时间一长，留存头脑中的还是两个公式r=和T=。遇到具体问题仍然力不从心，不能迅速入手。

建模是学习和探究物理的一个重要思想，可将其运用到磁偏转教学中。不妨对磁偏转问题中众多几何关系进行抽丝剥茧、归纳总结，引领学生建立几个常见的几何模型，并加以命名；这样不但方便了理解和记忆，而且头脑中有了几个模型存在，则解决问题的过程就是选用物理模型，使用模型，找出相应几何关系的过程。

带电粒子在匀强磁场中运动常见的几何关系如下：

1 勾股定理关系

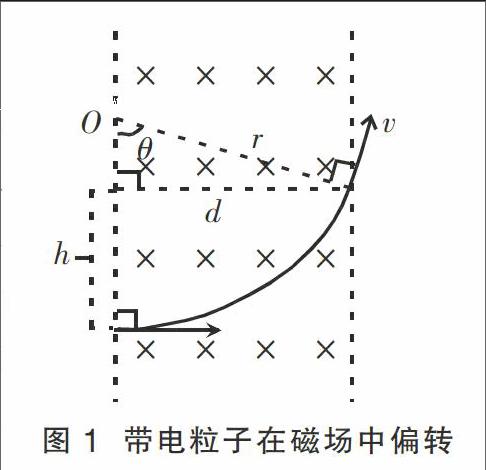
带电粒子从一个直线边界进入，再从另一个直线边界出去。通过作辅助线，总能找到与半径相关的直角三角形，如图1。

2 互余、互补关系

带电粒子从一个直线边界进入磁场，然后通过圆周运动再从该边界出磁场，由角的互余、互补以及几何对称特点，很容易看出运动的几何关系，如图2。

3 两圆相交

带电粒子进入圆形匀强磁场，再从磁场的圆边界出来，这种情形可以总结为两圆相交，即运动的圆与磁场圆相交，常考的有以下三种情形：

3.1 正切关系

带电粒子沿半径进入圆形匀强磁场，由几何对称可知，粒子一定沿半径方向射出磁场，如图3。

几何关系

3.2 正弦关系

带电粒子进出圆形匀强磁场，若要求运动时间最长，那么就是要求带电粒子在圆形磁场中跨度最大，而跨度最大的弦就是磁场圆的直径，如图4。

3.3 磁聚焦

带电粒子运动的圆与磁场圆相交，若它们的半径相等，则可以得到一种特殊关系既“磁聚焦”。如图5，在两圆交点分别作四条切线，由于对称它们构成菱形，则可以得到速度方向v∥QN。

这一关系进一步推广，得到结论：一束平行的带电粒子垂直射入圆形磁场，则带电粒子聚集于磁场圆形边界一点即“磁聚焦”；反之带电粒子束从圆形磁场边界一点发出，垂直经过磁场，则平行射出，如图6。

对于两圆相交的关系，教学过程中尤其要区分“运动圆”与“磁场圆”，只有“运动圆”才有

4 相切关系

带电粒子由一磁场进入另一磁场，则在两个磁场中运动的圆构成相切关系。两个圆心与切点共线，并且总能找到两个三角形相似或两个扇形相似。

4.1 内切关系

两个磁场的磁场方向相同，但磁感应强度大小不同，使得带电粒子在这两个磁场中运动的半径不同，构成内切关系。如图7，圆心O1、O2与切点C共线，ΔAO1C∽ΔDO2C。带电粒子从A点运动到D点，经过了两个磁场，空间位移为Δx=AD，在第一个磁场中r=、T1=，在第二个磁场中r=、T2=；所以在一个运动周期内有：

4.2 外切关系

两个磁场的磁场方向相反，则带电粒子在兩个磁场中的转动方向相反，两个“运动圆”构成外切关系。如图8，两圆相切，圆心O1、O2与切点P共线，扇形AO1P∽扇形PO1B，所以从A点进入磁场的v方向与从B点出磁场的方向相同。

5 结 语

针对带电粒子在匀强磁场中做匀速圆周运动所涉及到的各种几何关系，建立几个几何模型，这就相当于加工了几个零部件，然后对于各种磁偏转问题，引导学生去审视探究，看哪个零部件正好可以用上或给以启发，从而找到解决问题的突破口。这一物理思想的运用，极大地助推了学生的思维发展，培养了学生发现问题、解决问题的能力。

（栏目编辑 陈 洁）