简单导入 深度生成

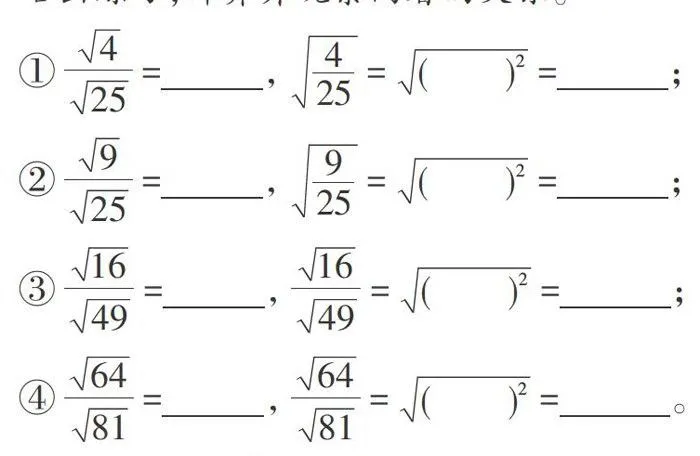
循序渐进是教育教学中的高频词汇，是指在学习中按照一定的步骤逐步深入和提高。众所周知，数学这门课程具有严密的逻辑结构，如果在教学中不能很好地贯彻循序渐进的原则，就不能使学生较为系统地学习和掌握所学知识点，从而容易产生模棱两可的概念。现以苏科版《数学》八（下）中的“12.2二次根式的乘除（3）”为例，来说明对新课的导入要尽可能简单，生成须是有深度的循序渐进的过程这一问题。

一、简单导入有利于学生体验学习过程。激发学习热情

师：同学们能回忆起上节课学习的二次根式的乘法法则及其积的算术平方根的性质吗？

师：大家还记得我们是怎么得到这些公式的吗？

生：不完全归纳法。

师：下面我们用这种方法来探究一下二次根式除法法则。

给出练习，计算并观察两者的关系。

师：从上面的式子，你能得到什么样的结论呢？

生：……

师：同学们能用字母把发现的规律表示出来吗？

设计意图：本节课的导入，从横向回忆二次根式的乘法法则和积的算术平方根的性质出发，通过简单的计算以及运用不完全归纳的方法，体验数学知识的探索和形成过程，让学生带着信心和热情来探索新知、发现新知，激发了学生的求知欲和学习动机，同时还起到了将前后知识进行联系的作用。因此，面对高度抽象而又有点乏味的数学学科，从简单入手，由浅入深，突出学生的学习主体地位，不失为一种培养学生学习兴趣和激发学生学习热情的有效方法。

二、知识点的二次呈现让生成变得深刻而有厚度

师：大家会证明这个公式吗？

学生纷纷摇头。

师：同学们能否仿照前面的公式名称，给这个公式也起个名字？

生：二次根式商的算术平方根的性质。

师：能不能用语言叙述一下这两个法则？

生：二次根式相除，开平方运算不变，被开方数相除。

生：商的算术平方根等于算术平方根的商。

设计意图：二次根式除法法则和商的算术平方根的性质的二次呈现，不少教师往往是忽略其推导过程的，而本节课的教学设计抓住这个二次呈现的机会，让学生体会知识的产生和发展过程，体会知识的来龙去脉；让学生感受到了数学的严密逻辑性，加深了对法则的理解；同时也自然地引出除法法则的逆运算以及它的合理性，使学生对这个知识点的认识变得深刻起来。

三、例题与练习层层深入，让新知逐步固化

师：下面让我们来看看今天学到的知识能够解决哪些问题？