次口径三层球缺药型罩形成串联EFP数值模拟

窦成彪，尹建平，徐全振，孙加肖，唐 琦

(中北大学 机电工程学院，太原 030051)



【装备理论与装备技术】

次口径三层球缺药型罩形成串联EFP数值模拟

窦成彪，尹建平，徐全振，孙加肖，唐 琦

(中北大学 机电工程学院，太原 030051)

运用ANSYS/LS-DYNA仿真软件，分析了一种次口径三层球缺药型罩战斗部形成串联EFP的过程，得到每层药型罩形成的EFP速度和长径比随球缺罩曲率半径、药型罩壁厚、装药高度的变化规律曲线。分析结果表明：球缺罩曲率半径和药型罩壁厚对EFP外形有显著影响，装药高度的增加可有效提高EFP速度。

三层药型罩；EFP；成型装药；数值模拟

多层串联式爆炸成形弹丸(explosively formed penetrators，EFP)战斗部是在复合装甲、爆炸反应装甲等新型装甲的基础上发展起来的新概念战斗部[1-2]。该战斗部可共轴放置药型罩，单次起爆后在同一轴线连续形成多个EFP。由于装药结构简单，能量利用率高，侵彻性能高等诸多优点，不少学者针对多层串联EFP进行了研究。Fong R等[3]对钢质双层和三层球缺罩战斗部进行成型实验，获得等效长径比很大的EFP。郑宇[4]建立了双层串联EFP的速度分析模型，分析了药型罩结构参数对双层罩形成串联EFP的影响。关于次口径三层罩装药结构对串联EFP 成型的影响规律，国内外很少报道。作者在双层药型罩形成EFP的基础上，设计了一种次口径装药三层药型罩战斗部。采用ANSYS/LS-DYNA软件，分析三层串联毁伤元的成型过程，研究了战斗部结构参数及装药参数对毁伤元成型的影响。

1 装药结构及计算模型

所设计的成型装药结构图如图1所示，其中装药直径80 mm，内罩曲率半径70 mm，三个药型罩(内罩、外罩、中间罩)均为次口径球缺型结构。该战斗部的三层药型罩厚度相等，共轴放置。三层相互接触的药型罩之间存在自由面，可以自由滑动和碰撞[5-7]。装药结构参数包括药型罩曲率半径R，药型罩总厚度T及装药高度H。

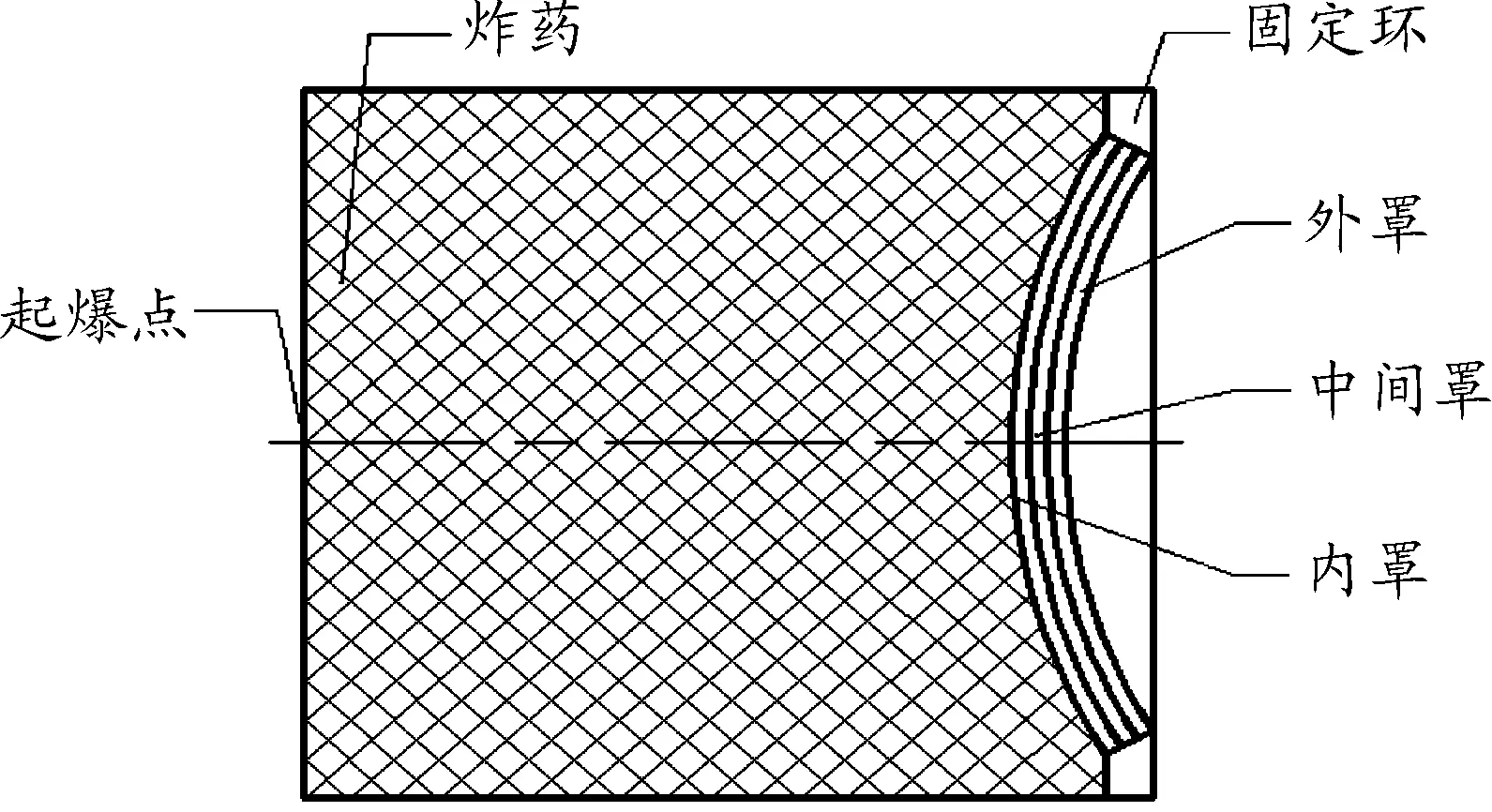
图1 战斗部结构简图

数值计算模型采用八节点六面体单元，如图2所示。划分的网格单元使用Lagrange算法，能够清楚地描述物质运动，真实地看到EFP 弹丸的成型过程。装药中炸药为8701炸药，采用HIGH_EXPLOSIVE_BURN材料模型和JWL状态方程；三个药型罩及固定环材料均为紫铜，本构模型选用Johnson Cook模型，状态方程为Gruneisen方程[8]。所用材料模型如表2所示，仿真采用装药端面中心点起爆。

图2 计算模型

名称材料状态方程本构模型装药8701JWL—内罩紫铜GruneisenJohnsonCook中罩紫铜GruneisenJohnsonCook外罩紫铜GruneisenJohnsonCook固定环紫铜GruneisenJohnsonCook

2 三层串联EFP成型过程

为分析三层罩成型过程，选取内罩曲率70 mm，装药高度80 mm，每层药型罩厚度1.8 mm。图3为起爆后不同时刻的三层串联EFP成型过程，可以看出：炸药起爆后，爆轰波首先到达药型罩中间部分，使三个药型罩相互碰撞，此时药型罩顶部轴向速度均大于底部轴线速度，各个药型罩向后翻转。由于药型罩之间为自由表面以及在厚度方向存在速度差，相互接触的药型罩底部边缘之间开始出现分离。此后，药型罩轴线附近微元在径向速度的作用下向轴线汇聚，内罩与中罩、中罩与外罩轴线因速度差且相互没有牵连发生分离；药型罩底部由于径向速度低，相互接触，未发生分离。最后，由于药型罩微元之间的相互牵连作用，尾部速度提高，各接触的药型罩在翻转的过程中逐渐分离。150 μs后EFP不再互相接触，分离后的药型罩成型与单层药型罩形成EFP类似。最终，成型的三个EFP具有恒定的速度差，形成共轴的三层串联EFP。图4显示成型过程中各EFP头部速度变化。

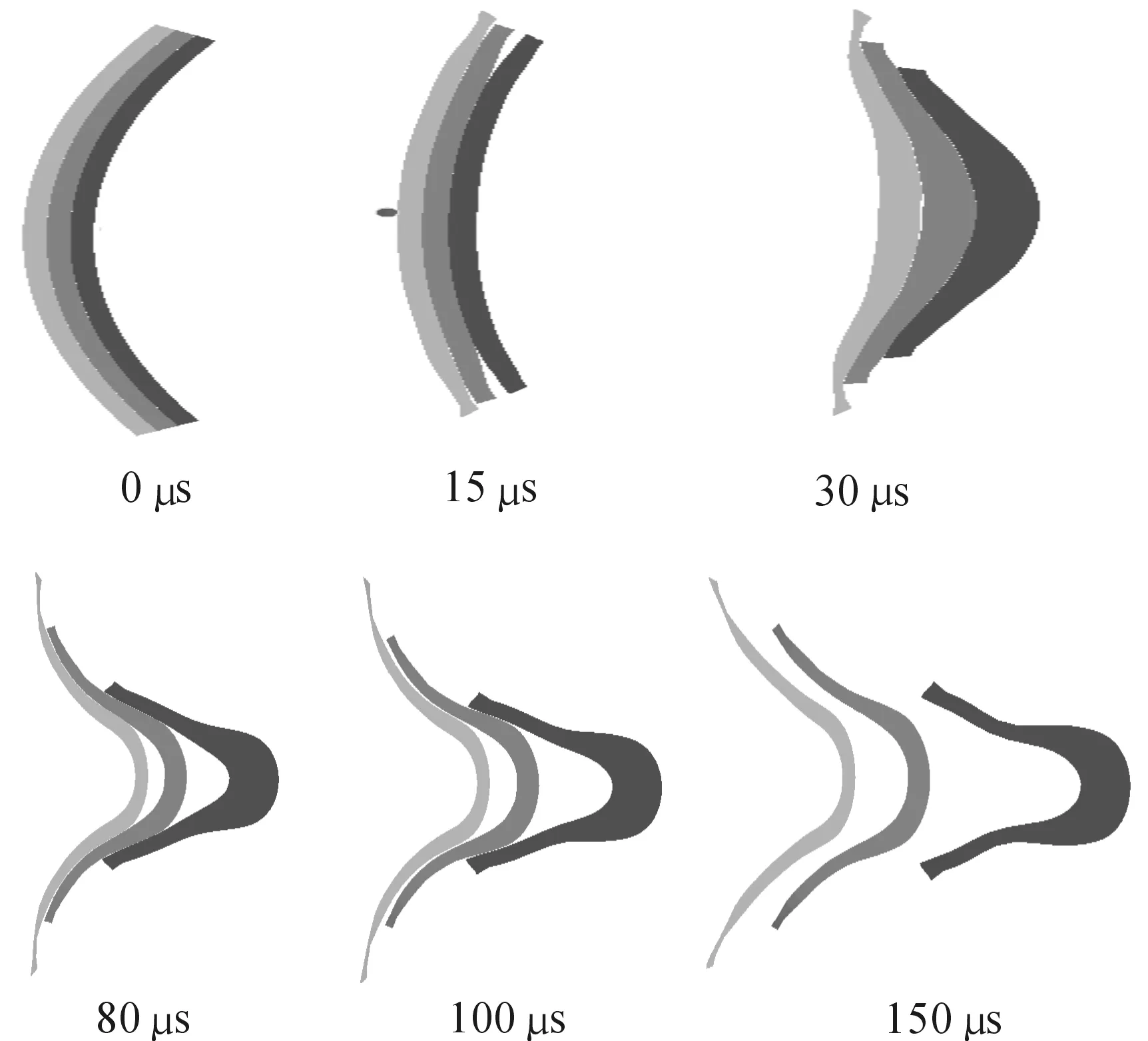
图3 不同时刻仿真结果

图4 EFP头部速度变化

3 结构参数对成型影响

3.1 曲率半径的影响

单层球缺药型罩的曲率半径是影响EFP成型的重要因数。由于三层药型罩结构中药型罩互相贴合放置，每层药型罩曲率半径相互关联，由内向外呈线性梯度减小。为分析曲率半径的影响，取每层药型罩壁厚1.8 mm，装药高度80 mm，分别计算了内罩曲率半径为60、65、70、75、80 mm，300 μs后的EFP成型参数，如表2所示。

300 μs后的EFP速度基本稳定，EFP之间形成稳定速度差， EFP速度、长径比随曲率半径变化曲线如图5和图6。曲率半径对三层药型罩的的分离程度影响很大，在三种曲率半径下，外罩与中罩都能快速分离。曲率半径越小，内罩与中罩分离越迅速，这是由于曲率半径较大时,内罩与中罩形成EFP尾裙发生了碰撞，两EFP之间速度差减小；当曲率半径减小时,碰撞现象减弱，速度差增大。且内外罩的速度差随着曲率半径的增加而减小。分析EFP成型参数可知，曲率半径对成型的影响与单层球缺药型罩的影响不同，每层药型罩变化趋势也各不相同。曲率半径增大，内罩与中罩形成的EFP速度增大，而外罩的速度变化不大。另一方面，曲率半径对外罩长径比影响最为明显，R从80 mm减少到60 mm，外罩形成EFP长径比增加一倍，内罩减少一半，而中罩变化不大。

表2 EFP成型参数

图5 EFP速度随曲率半径变化

3.2 药型罩总壁厚的影响

根据学者对单层球缺药型罩EFP的研究，药型罩壁厚对EFP速度影响很大。对三层药型罩而言，EFP之间的稳定速度差，是形成串联EFP的必要条件。由曲率半径对成型影响分析，选择曲率半径R为70 mm，装药高度80 mm。三层药型罩厚度相同条件下，分别计算每层壁厚为1.4、1.6、1.8、2.0、2.2 mm，300 μs后EFP成型参数如表3所示。EFP速度、长径比随药型罩厚度变化曲线如图7和图8所示。

由图7和图8可以看出，随着药型罩壁厚的增大，每个微元的压垮速度都下降，每层药型罩形成的EFP长径比和速度均减少。外罩与中罩比较，速度差增大；但中罩与内罩的速度差减小。当每层厚度为1.4 mm时，由于壁厚太薄，成型翻转过程中，罩体被拉断，不能正常分离；每层厚度2.2 mm时，三个药型罩抗变形能力都明显增强，药型罩分离迅速，内罩速度过低，不能形成形状较好的杆式EFP。

综上所述，形成正常分离的串联EFP，药型罩总厚度选择不宜过大或过小，每层药型罩厚度为1.8～2.0 mm时，可形成长径比较大的三层杆式EFP。

3.3 装药高度的影响

为分析装药高度对三层药型罩串联EFP参数的影响，选择每层药型罩壁厚1.8 mm，曲率半径R为70 mm，分别计算装药高度为60、70、80、90、100 mm结果如图所示。EFP速度、长径比随曲率半径变化曲线如图9和图10所示。

由表4可以看出，在不同装药高度时，三层药型罩均能实现分离成型。由图9可知，随着装药高度的增加，每层EFP速度增加，其中外罩速度增加最大，每层EFP之间速度差变大；同样，随着装药长径比增加，每层EFP长径比及长度增大。综合分析可知，装药高度对三层串联EFP影响规律与单层EFP类似，装药量的增大使EFP获得更多动能，使EFP拉伸时间变长。

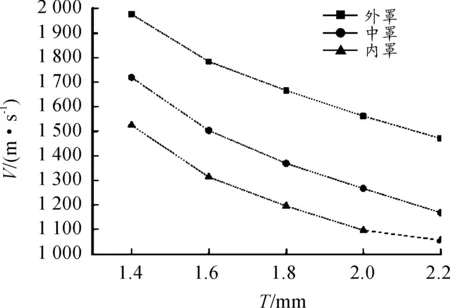
图7 EFP速度随药型罩厚度变化

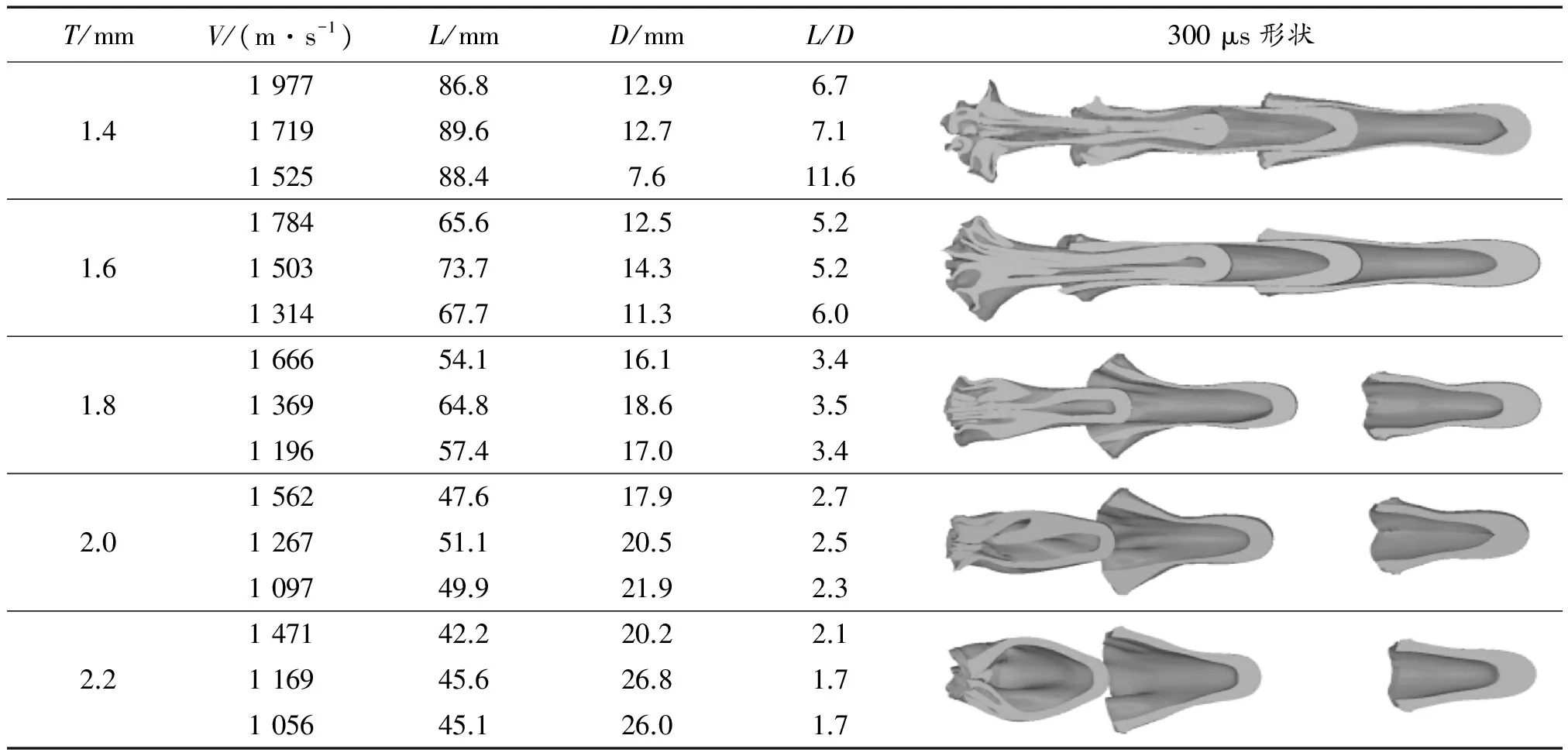
T/mmV/(m·s-1)L/mmD/mmL/D300μs形状1．4197786．812．96．7171989．612．77．1152588．47．611．61．6178465．612．55．2150373．714．35．2131467．711．36．01．8166654．116．13．4136964．818．63．5119657．417．03．42．0156247．617．92．7126751．120．52．5109749．921．92．32．2147142．220．22．1116945．626．81．7105645．126．01．7

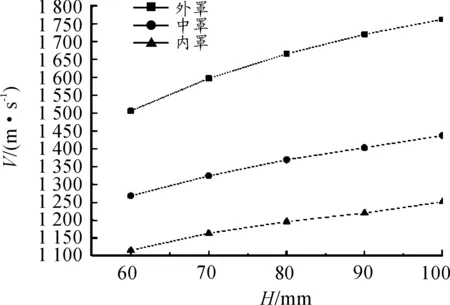
图9 EFP速度随装药高度变化

H/mmV/(m·s-1)L/mmD/mmL/D300μs形状60150643．519．42．2126848．119．92．4111549．218．62．670159748．816．72．9132455．818．73．0116352．218．42．880166654．116．13．4136964．818．63．5119657．417．03．490172159．216．23．7140368．915．14．6122061．615．73．9100176362．913．64．6143782．313．26．2125168．114．44．7

4 结论

1) 采用的三个同材料等壁厚球缺型药型罩同轴贴合放置并采用次口径成型装药结构的方法形成三个独立共轴EFP，各EFP之间具有稳定的速度差。

2) 成型装药结构参数(球缺罩曲率半径、药型罩壁厚、装药高度的变化规律)对三层药型罩分离形成独立EFP影响不同。其中，曲率半径主要影响EFP形状，对外层药型罩速度影响不大；每层药型罩壁厚越大，各层药型罩分离越快，过小的药型罩厚度不能分离成独立EFP，过大的厚度由于内药型罩速度低不能形成杆式EFP；三层药型罩装药高度和长径比对每层EFP速度的影响规律与单层药型罩类似，可通过增加装药高度提高每层EFP速度。

[1] 龙源,毛振兴,刘健峰，等.曲率半径对双层药型罩EFP战斗部成形及侵彻的影响 [J].爆破器材,2016，45(3):5-10.

[2] 蒋建伟，杨军，门建兵，等.结构参数对EFP成型影响的数值模拟 [J].北京理工大学学报，2004，24(11)：939-942.

[3] FONG R,NG W,WEIMAN K.Testing and analysis of multi-liner EFP warheads[C]//20th International Symposium of Ballistics,2002：578-582.

[4] 郑宇.双层药型罩毁伤元形成机理研究 [D].南京:南京理工大学，2008.

[5] 孙加肖，尹建平，王志军，等.双层椭圆形药型罩装药射流成形时长短轴比、铝铜铁三种材料的声阻抗和罩间距三因素正交设计研究 [J].兵器装备工程学报，2016，37(6)：135-139.

[6] 孙华，王志军.新型双层药型罩形成毁伤元数值模拟与分析 [J].弹箭与制导学报，2013，33(1)：70-72.

[7] 刘健峰，龙源，纪冲，等.双层药型罩EFP战斗部性能参数的灰色系统理论分析及实验研究 [J].含能材料，2016，24(8)：728-734.

[8] CHANG B H，YIN J P，CUI A Q，et al.Improved Dynamic Mechanical Properties of Modified PTFE Jet Penetrating Charge with Shell [J].Strength of Materials，2016，48( 1)：82-89.

(责任编辑 周江川)

Numerical Simulation of Shaped Charge with TripleSub-Caliber Hemispherical Liner into Series EFP

DOU Cheng-biao,YIN Jian-pin,XU Quan-zheng,SUN Jia-xiao,TANG Qi

(School of Mechatronic Engineering，North University of China，Taiyuan 030051，China)

By ANSYS/LS-DYNA software, the forming process of shaped charge with triple sub-caliber hemispherical liner into series EFP was analyzed. The law curves of velocity and L/D with structural parameters of curvature radius, thickness of hemispherical liner and the height of shaped charge of each liner were obtained. The result indicates that there are remarkable effects of curvature radius and thickness of hemispherical liner on the formation parameters of each EFP. Increasing the height of shaped charge effectively enhances velocity of each EFP.

triple layer liners; EFP; shaped charge; numerical simulation

2016-11-25；

2016-12-31

国家自然科学基金( 11572291)

窦成彪(1990—)，男，硕士研究生，主要从事冲击动力学及仿真研究。

10.11809/scbgxb2017.04.014

窦成彪，尹建平，徐全振，等.次口径三层球缺药型罩形成串联EFP数值模拟[J].兵器装备工程学报，2017(4):63-67.

format:DOU Cheng-biao,YIN Jian-pin,XU Quan-zheng,et al.Numerical Simulation of Shaped Charge with Triple Sub-Caliber Hemispherical Liner into Series EFP[J].Journal of Ordnance Equipment Engineering,2017(4):63-67.

TJ413

A

2096-2304(2017)04-0063-05