伪补Ockham代数核理想同余关系的注记

赵秀兰， 陈丽娟

(1.黄河科技学院数理部， 郑州450063；2.河南工程学院理学院， 郑州451191)

伪补Ockham代数核理想同余关系的注记

赵秀兰1， 陈丽娟2

(1.黄河科技学院数理部， 郑州450063；2.河南工程学院理学院， 郑州451191)

Ockham代数；伪补Ockham代数；理想；核理想；同构

Blyth和Varlet首次在文献[1]中研究了伪补Ockham代数(L;∧,∨,f,*0,1)，简称pO代数，它是一个(2,2,1,1,0,1)类型的代数类，是在有界分配格上赋予两个一元运算f,*的代数，(L;∧,∨,f,0,1)∈O,(L;∧,∨,*0,1)∈p且一元运算f,*满足交换律(p代数，Ockham代数，pO代数的详细信息见文献[2-5])。在泛代数研究领域，对代数结构的研究，一直是本专业学者关注的方向。借助理想和滤子是认识Ockham代数类的结构及同余关系的一个重要工具，特别是核理想与余核滤子，根据核理想与余核滤子同余关系反映Ockham代数类的结构见文献[6-14]。在文献[6]中，作者借助核理想与余核滤子的同余关系刻画了伪补Ockham代数的结构。本文将在文献[6]的基础上，进一步的探讨、刻画伪补Ockham代数核理想同余关系的性质特征，反映伪补Ockham代数属性。

1基本知识

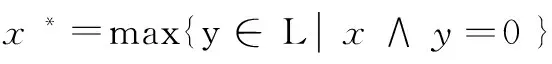
定义2[15]设(L;∧,∨)是一个格，I是格L的子格，若x,y∈L，y≤x∈I总有y∈I，称子格I是格L的理想。

定义3[1]设(L;∧,∨,0,1)是一个有界分配格，其上赋予两个一元运算*和f，且(1)(L;*)∈p;(2)(L;f)∈O;(3)(x∈L)f(x*)=[f(x)]*,称(L;∧,∨,*,f,0,1)是伪补Ockham-代数(简称pO-代数)。

定义4[6]设(L;∧,∨,f,*,0,1)∈pO，θ是L的一个格同余关系，若(x,y)∈θ⟹(x*,y*)∈θ,(f(x),f(y))∈θ，则称θ是L的同余关系。符号ConL表示L的全体同余关系构成的集合。

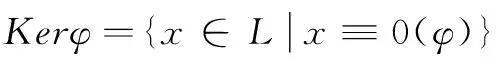
引理1[6]设L∈pO，I是L的理想，则下面的条件成立：I是L的核理想当且仅且(∀a∈L)a∈I⟹a**,f(a*)∈I。

引理2[6]设L∈pO，I是L的核理想，则I=KerRI，其中同余关系RI定义为：(x,y)∈RI⟺(∃a∈I)x∧a*=y∧a*。

设(L;∨,∧,f,*)是一个伪补Ockham代数，在文献[6]中，由核理想I能构造一个与核理想对应的同余关系，那么，核理想与核理想对应的同余关系能否构成一一对应。

2主要结果

设L∈pO，符号I(L),Ik(L)分别表示L的理想和核理想构成的集合，则I(L),Ik(L)之间存在下列关系。

定理1Ik(L)是I(L)的一个子格。

证明令I,J∈Ik(L)，下证I∧J,I∨J∈Ik(L)。

设x∈I∧J,则x∈I,x∈J。又因I,J∈Ik(L)，由引理1知，x**,f(x*)∈I且x**,f(x*)∈J，故x**,f(x*)∈I∧J，又由引理1知，I∧J∈Ik(L)。

令x∈I∨J，由引理1知，存在i∈I及j∈J使得x≤i∨j。由文献[6]知，x**≤i**∨j**和f(x*)≤f(i*)∨f(j*)，又因I,J∈Ik(L)，所以由引理1知，i**∈I,f(i*)∈I且j**∈J,f(j*)∈J。因此x**,f(x*)∈I∨J。从而由引理1得I∨J∈Ik(L)。所以Ik(L)是I(L)的一个子格。

设L是一个伪补Ockham代数，I是L的一个核理想，具有核理想I的最小同余关系RI，沿用文献[6]中的定义，即(x,y)∈RI⟺(∃a∈I)x∧a*=y∧a*。设L∈pO，θ,φ∈ConL，定义L上的一个等价关系，(x,y)∈θ°φ⟺(∃z∈L)(x,z)∈θ,(z,y)∈φ。显然，θ°φ是L上的同余关系。

若θ,φ∈ConL，且θ,φ满足关系式θ°φ=φ°θ，则称同余关系θ,φ具有同余置换性。对于任意的I,J∈Ik(L)，则RI,RJ具有同余置换性。

定理2设L是一个伪补Ockham代数，I,J∈Ik(L)，则RI°RJ=RJ°RI。

证明假设(x,y)∈RI°RJ,则存在z∈L，使得(x,z)∈RI,(z,y)∈RJ，于是存在i∈I,j∈J，有x∧i*=z∧i*,z∧j*=y∧j*，所以x∧i*∧j*=y∧i*∧j*。

令s=(x∧j*)∨(y∧i*)，从而可得

同理可证，RJ°RI⊆RI°RJ。所以，RI°RJ=RJ°RI。

下面，探讨伪补Ockham代数的核理想及其同余关系之间的联系。

定理3设L是一个伪补Ockham代数，I,J∈Ik(L)，则I⊆J⟺RI⊆RJ。

证明设I,J∈Ik(L)，I⊆J，根据RI,RJ的定义，可得RI≤RJ。

另一方面，设I,J∈Ik(L)，RI≤RJ，则KerRI≤KerRJ。由引理2知，I=KerRI,J=KerRJ，所以I⊆J。定理得证。

定理4设L是一个伪补Ockham代数，则Ik(L)≅Ck(L)。

证明显然，R{0}=ω(相等关系)及RL=ι(泛同余关系)。

先证对任意的I,J∈Ik(L)，有RI∧RJ=RI∧J。由定理1知，I∧J∈Ik(L)。因为I∧J≤I,I∧J≤J，故由定理3知，RI∧J≤RI,RI∧J≤RJ，所以RI∧J≤RI∧RJ。

设(x,y)∈RI∧RJ，由文献[15]知，(x,y)∈RI且(x,y)∈RJ。因此存在i∈I,j∈J使得x∧i*=y∧i*,x∧j*=y∧j*，于是有x∧(i∧j)*=y∧(i∧j)*，又因i∧j∈I∧J，所以(x,y)∈RI∧J，故RI∧RJ≤RI∧J，所以RI∧RJ=RI∧J。

证对任意的I,J∈Ik(L)，有RI∨RJ=RI∨J。由定理1知，I∨J∈Ik(L)。由于I∨J≥I,I∨J≥J，由定理3知，RI∨J≥RI,RI∨J≥RJ，所以RI∨J≥RI∨RJ。

设(x,y)∈RI∨J，则存在i∈I及i∈J使x∧i*∧j*=y∧i*∧j*，于是有

因此(x,y)∈RI∨RJ，从而有RI∨J≤RI∨RJ，故RI∨RJ=RI∨J。又因RI=RJ当且仅当I=KerRI=KerRJ=J，因此映射：I→RI建立起Ik(L)→Ck(L)的一一对应，所以Ik(L)≅Ck(L)。

3结束语

本文在文献[6]的基础上，对伪补Ockham代数的核理想同余关系作了一个补充，借助伪补Ockham代数的核理想判别定理以及具有核理想同余关系表达式，获得了伪补Ockham代数核理想及其同余关系同构的结论。这一结论有助于了解伪补Ockham代数的代数结构。

[1] BLYTH T S,FANG J,VARLET J C.Ockham algebras with pseudocomplementation[J].Communications in Algebra,1997(25):3605-3615.

[2] BLYTH T S,VARLET J C.Ockham algebras[M].Oxford:Oxford University Press,1994.

[3] FANG J.Distributive Lattices with Unary Operations[M].北京:科学出版社,2011.

[4] FANG J,WANG T.De Morgan algebras with double demi-pseudocomplementation[J].Acta Mathematica Scientia,2011,31B(4):1613-1623.

[5] BLYTH T S,FANG J.On the endomorphisms of Ockham algebras with pseudocomplementation[J].Studia Logica,2011,98:237-250.

[6] 方捷,吴丽云.拟补Ockham代数的理想与滤子[J].数学学报,2004,47(4):647-652.

[7] 罗从文.MS-代数的核理想[J].应用数学,2001,14(1):39-41.

[8] 张小红,刘三阳,刘用麟.伪MIL-代数(WPBL-代数)的正则滤子[J].西安电子科技大学学报:自然科学版,2006,33(5):829-832.

[9] 方捷,沈吓妹.平衡半伪补Ockham代数的滤子[J].模糊系统与数学,2010,24(3):38-45.

[10] 王雷波,方捷.几乎伪补格的核理想与W-理想[J],模糊系统与数学,2012,26(1):61-66.

[11] 牛超群,吴洪博.BRo代数中的*理想及其诱导的商代数[J].江西师范大学学报:自然科学版,2013,37(3):221-224.

[12] 赵秀兰,马红娟,初元红,等.双重半伪补de Morgan代数的滤子同余关系[J].模糊系统与数学,2015,29(4):19-26.

[13] 赵秀兰,史西专.半伪补MS代数的理想及同余关系[J].模糊系统与数学,2016,30(2):57-63.

[14] 赵秀兰,蒋红敬.平衡伪补Ockham代数的O理想[J].汕头大学学报,2016,31(4):19-23.

[15] GRATZER G.Lattice Theory[M].New York:W.H.Freeman and Company,1971.

A Note on the Ideal Congruence Relations on Pseudocomplement Ockham Algebras

ZHAOXiulan1,CHENLijuan2

(1.Department of Mathematics and Physics, Huanghe Science and Technology College, Zhengzhou 450063, China; 2.College of Science, Henan Institute of Engineering, Zhengzhou 451191, China)

Ockham algebra; pseudocomplemented Ockham algebra; ideal; kernel ideal; isomorphism

2017-01-16

国家自然科学基金(11302072)

赵秀兰(1982-)，女，河南商水人，副教授，硕士，主要从事序代数结构方面的研究，(E-mail) xiulanz@126.com

1673-1549(2017)02-0098-03

10.11863/j.suse.2017.02.19

O153.1

A