基于模糊数的案均赔款模型
张静


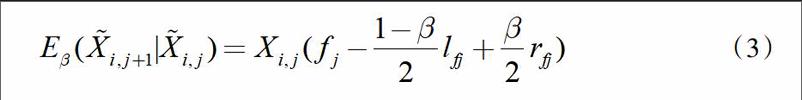
摘 要:在传统案均赔款模型中引入非对称的模糊数,对进展因子和结案率进行重新估计,从而得到未决赔款准备金的新估计。模糊案均赔款模型可以通过模糊进展因子和模糊结案率的范围确定最终赔款预测的不确定性,并可以对感兴趣的变量的不确定性进行计算,解决了无法度量准备金估计量的波动性问题。
关键词:模糊数;案均赔款模型;赔款准备金
1 概述
随着保险业的迅速发展,对保险行业中负债经营的研究也逐年增加,其中最大的负债就是赔款准备金。如果对准备金估算不及时、不精确,保险公司的正常经营将会受到严重影响,甚至会出现破产危机,因此合理估计索赔准备金对保险公司来说至关重要。
对于未决赔款准备金的估计有诸多方法,其中案均赔款法相比于传统链梯法既考虑了赔款数据信息又考虑案件数信息,使评估信息更加充分。但传统案均赔款法作为一种确定性方法只能得到赔款准备金的均值估计,无法度量波动性,对于不确定性风险的度量是不充分的,因此,本文将非对称三角模糊方法应用到案均赔款模型中,用模糊因子的范围确定模型估计的不确定性,提高赔款准备金的准确度,为保险公司预留准备金提供依据。
2 传统案均赔款模型
案均赔款法需要分别对案件数和案均赔款应用链梯法得出各事故年的未决赔款准备金。根据是否已结案分为已报案案均赔款和已结案案均赔款。本文针对已报案均赔款法进行改进。
已报案均赔款法应用累计已报案赔款数据Ci,j和累计已报案案件数Ni,j进行准备金估计。具体步骤总结为:
步骤一:计算已报案案均赔款。将累计已报案赔款与累计已报案案件数相除,计算已报案案均赔款Xi,j流量三角形,计算公式如公式(1)所示:
步骤二:计算已报案均赔款流量三角形的逐年进展因子fi,j,选取平均值作为进展因子的选定值。其中,逐年进展因子fi,j可用公式(2)表示:
步骤三:预测已报案案均赔款流量三角形的下三角部分。与链梯法类似,根据已报案案均赔款流量三角形的进展因子平均值即可预测其下三角部分。
步骤四:预测最终案件数。对累计已报案案件数流量三角形使用链梯模型,预测各事故年的最终索赔次数。
步骤五:预测未决赔款准备金。各事故年的未决赔款准备金等于各事故年最终赔款减去已决赔款金额。
3 模糊案均赔款模型
将非对称的模糊数和传统的已结案均赔款模型结合预测最终的索赔准备金,并得到预测值的不确定性估计。
模型假设存在三角模糊数使得各发展年的赔付额之间有稳定的比例关系,且增量赔款是后一进展年数据减去前一进展年数据的赔款值。则模糊案均赔款模型有下式成立:
其中,i,j和j是正的模糊数,i,j为已观测数据,所以i,j=Xi,j。三角模糊数j的估计值 ,其中
同样的,对累计已报案案件数流量三角形使用链梯模型时,其中的赔款案件数进展因子和累计已报案件数也符合上述公式。
最终求得的累计赔款准备金预测值如公式(8)所示。
4 模糊案均赔款模型中预测值的不确定性
在上述模型中,案均赔款数据中进展因子的模糊估计量满足公式(9)。
同样地,累计已报案数据中模糊进展因子也符合(9)式。
我们给定观测值 和一参数N属于正实数,则最终赔款的预测值为
最终赔款的不确定性为
通过不确定性范围的预测来有效估计最终赔款數据的区间波动性,进而能得到更加可靠、精确的保险赔款数据。
参考文献
[1]陈静仁,王玉文.模糊数在链梯法索赔准备金中的应用[J].数学的实践与认识,2015(17):106-112.
[2]范英,李辰,晋民杰,等.三角模糊数和层次分析法在风险评价中的应用研究[J].中国安全科学学报,2014(07):70-74.
[3]孟生旺.非寿险准备金评估的广义线性模型[J].统计与信息论坛,2009(06):3-7.

