KDP晶体单点金刚石飞切轨迹波纹误差辨识研究*
阳 红, 王宝瑞, 吉 方, 刘有海, 夏 欢, 陈东生
(中国工程物理研究院机械制造工艺研究所 绵阳,621900)
KDP晶体单点金刚石飞切轨迹波纹误差辨识研究*
阳 红, 王宝瑞, 吉 方, 刘有海, 夏 欢, 陈东生
(中国工程物理研究院机械制造工艺研究所 绵阳,621900)
频率辨识是消除或抑制KDP晶体超精密金刚石飞切轨迹波纹误差的重要前提。针对该问题,提出了一种基于空间频率变换的飞切轨迹波纹误差辨识方法。该方法通过提取表面飞切轨迹上的轮廓幅值,计算其波纹误差的空间频率,然后采用飞切线速度进行转换,获得时间域上的频率值,实现波纹误差特征频率的准确分离。将误差特征频率与切削振动频率、机床气浮主轴系统的固有频率进行对比分析,明确了气浮主轴在断续切削力作用下产生的自激振动和来自电机的受迫振动是导致KDP晶体金刚石飞切波纹误差的根本原因。在此基础上,通过对主轴驱动及结构的优化,工艺实验结果表明,大口径KDP晶体飞切后的PSD1(2.5~33 mm)频段内波纹误差RMS值由53 nm降低至12 nm。
金刚石飞切; 波纹误差; 空间频率; KDP晶体
1 问题的引出
金刚石飞切以其高精度、高效率、低成本等众多优点,在国防科技、光通信、机械电子和生物医学等领域都显示出了极其重要的应用价值[1]。例如,在惯性约束核聚变、固体激光驱动器、强激光武器等重大装备中,KDP晶体起着非常重要的作用,金刚石飞切克服该晶体材料质地软、易潮解、脆性高、高温度敏感性等特点,是从事精密加工的最有效手段[2]。
但在金刚石飞切加工过程中,受机床振动、切削颤振、环境等多种因素的影响,加工件表面将残留大量的不同频率的波纹误差,如图1所示。在光学系统中该误差将导致光束分散,并极易造成光学元件的损伤[3],因此必须严格控制。

图1 金刚石飞切表面及波纹误差Fig.1 Wavniess error of diamond fly cutting surface
要控制图1所示波纹误差,首先必须对该误差形貌的组成成分进行准确分离,以辨识该误差的来源。传统的方法大多采用中线制来分离加工表面高频与中、低频表面信息,采样长度是原始轮廓上的等间隔长度,由于没有考虑表面的局部特征,且存在相位扭曲与边界效应,因此往往会产生错误的结果[4]。Lou等[5]以原始表面测量数据作为输入,采用Motif方法通过设定不同的分离阈值成功提取了表面3 个粗糙度和 4 个波纹度表征参数。但该方法获取的是表面形貌的平均参数,无法实现波纹误差的分离。为了将加工表面上的波纹误差频率分离出来,并对表面进行全频段分析,近年来Zhang等[6]采用功率谱密度(power spectral density,简称PSD)定量地计算出加工表面不同频率形貌信息的分布。陈东菊等[7]采用小波变换实现了金刚石切削表面形貌的多尺度分解与合成,获得了表面主要频率特征的空间形态及其对原始形貌的影响程度。上述方法对分析金刚石飞切表面波纹误差的组成成分提供了有益探索,但由于并未转换为时间域上的频率值,因此无法与机床切削过程中的振动信号关联起来,对波纹误差的溯源及抑制难以提供有效支撑。
为了实现超精密金刚石飞切波纹误差的辨识与溯源,进而消除或抑制波纹误差,首先介绍一种基于空间频率变换的波纹误差辨识方法。笔者应用该方法于超精密金刚石飞切加工表面波纹误差的分离中,获取飞切圆弧轨迹上的误差频率成分,进而与切削振动和主轴模态实验相结合实现了误差频率成分的溯源。最终,通过机床优化使PSD1(2.5~33 mm)频段内波纹误差RMS值显著降低。
2 超精密金刚石飞切轨迹波纹误差分离2.1 空间频率概念及计算
空间频率是指细节特征在单位长度上的重复次数[8]。目前,国内外研究人员有利用空间频率这一分析方法对加工表面进行滤波、表征和评价方面的研究[9],但未见在超精密单点金刚石飞切波纹误差辨识方面的应用。
空间频率是根据傅里叶提出的振动波形分析理论而出现的,其计算过程如下:设图1(b)为非周期性函数F(x),在数学分析中,该函数可以用频率为连续变化的简谐函数的积分来表示
(1)
(2)
函数f(w)称之为函数F(x)的频谱,式(1)为函数F(x)的傅里叶变换,式(2)为傅里叶逆变换,F(x)和f(w)构成了傅里叶变换对。
实质上,F(x)和f(w)描述的是同一个物理量,F(x)表述在空间坐标中,x代表位置,设单位为mm。f(w)表述在频率坐标中,w代表空间频率,设单位为mm-1。
在金刚石飞切波纹误差分析中,为方便可进一步将空间域频率f(w)变换到时间域频率f(t)
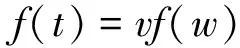
(3)
其中:v为金刚石飞切线速度,单位为mm/s;f(t)为变换后的频率,单位为Hz。
根据f(t)值,即可与机床加工过程中的振动信号频率进行对比,辨识波纹误差的来源。
2.2 基于飞切圆弧轨迹的波纹误差提取
为了对超精密金刚石飞切轨迹上的波纹误差展开分析,首先采用Matlab编程提取了Zygo激光干涉仪测量得到的超精密金刚石飞切表面数据(150 mm×150 mm),如图2所示。在此基础上,通过对切削轨迹进行搜索,最终提取到的飞切圆弧形轨迹上的轮廓幅值如图3所示。

图2 飞切面形测量数据Fig.2 Measurment data of fly cutting surface

图3 飞切表面轮廓Fig.3 Profile of fly cutting surface
由图2可知,飞切表面在进给和切削方向上均存在波纹误差。为了实现飞切轨迹上波纹误差的准确分离和辨识,必须提取其圆弧形切削轨迹上的轮廓幅值,以避免图1所示按直线轮廓提取时包含进给方向的波纹误差。按飞切轨迹和直线提取到的飞切表面轮廓值如图3所示。直线轨迹轮廓波纹误差幅值由于包含了进给方向的波纹误差,因此比飞切轨迹轮廓上的波纹误差值偏大。
2.3 波纹误差频率计算
在获得飞切轨迹上的波纹误差幅值后,通过式(1)计算其空间频率,得到图3所示飞切圆弧轨迹上的波纹误差空间频率分布,如图4所示。
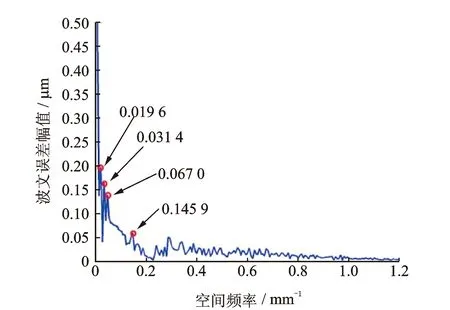
图4 飞切轨迹波纹误差空间频率Fig.4 Spatial frequencies of fly cutting waveness error
为保持切削深度与进给速度不变,采用不同主轴转速加工获得的飞切轨迹上的空间频率分布情况,如表1所示。
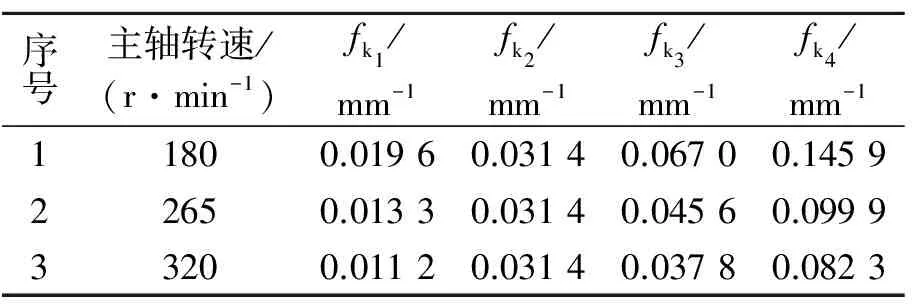
表1 飞切轨迹波纹误差空间频率
在获得飞切轨迹波纹误差空间频率的基础上,利用式(3)可将空间频率转化为时间域上的频率值,如表2所示。由此实现了飞切轨迹波纹误差的分离。
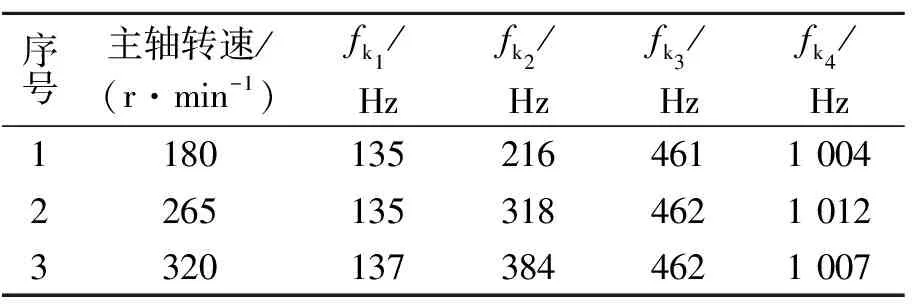
表2 飞切轨迹波纹误差频率
3 超精密金刚石飞切轨迹波纹误差辨识
3.1 飞切振动信号测量及处理
为了实现表2所示飞切表面波纹误差频率的溯源,笔者在自研的超精密金刚石飞切机床DFC-600A上开展了飞切振动信号测量,实验机床如图5所示。该机床采用高精度气浮主轴和液体静压导轨,最大可实现500 mm×500 mm零件超精密加工。

图5 超精密金刚石飞切机床DFC-600AFig.5 Ultraprecision fly cutting machien DFC-600A
实验用飞切KDP晶体尺寸为150 mm×150 mm×10 mm,加速度传感器采样频率设为5 000 Hz。图6所示为切削深度3 μm、进给速度4 mm/min、主轴转速180 (r·min-1)时测量得到的飞切周期性振动信号。在单个周期内飞切振动信号如图7所示。
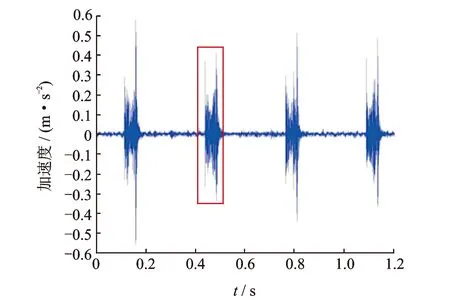
图6 飞切周期性振动信号Fig.6 Cyclical vibration of fly cutting
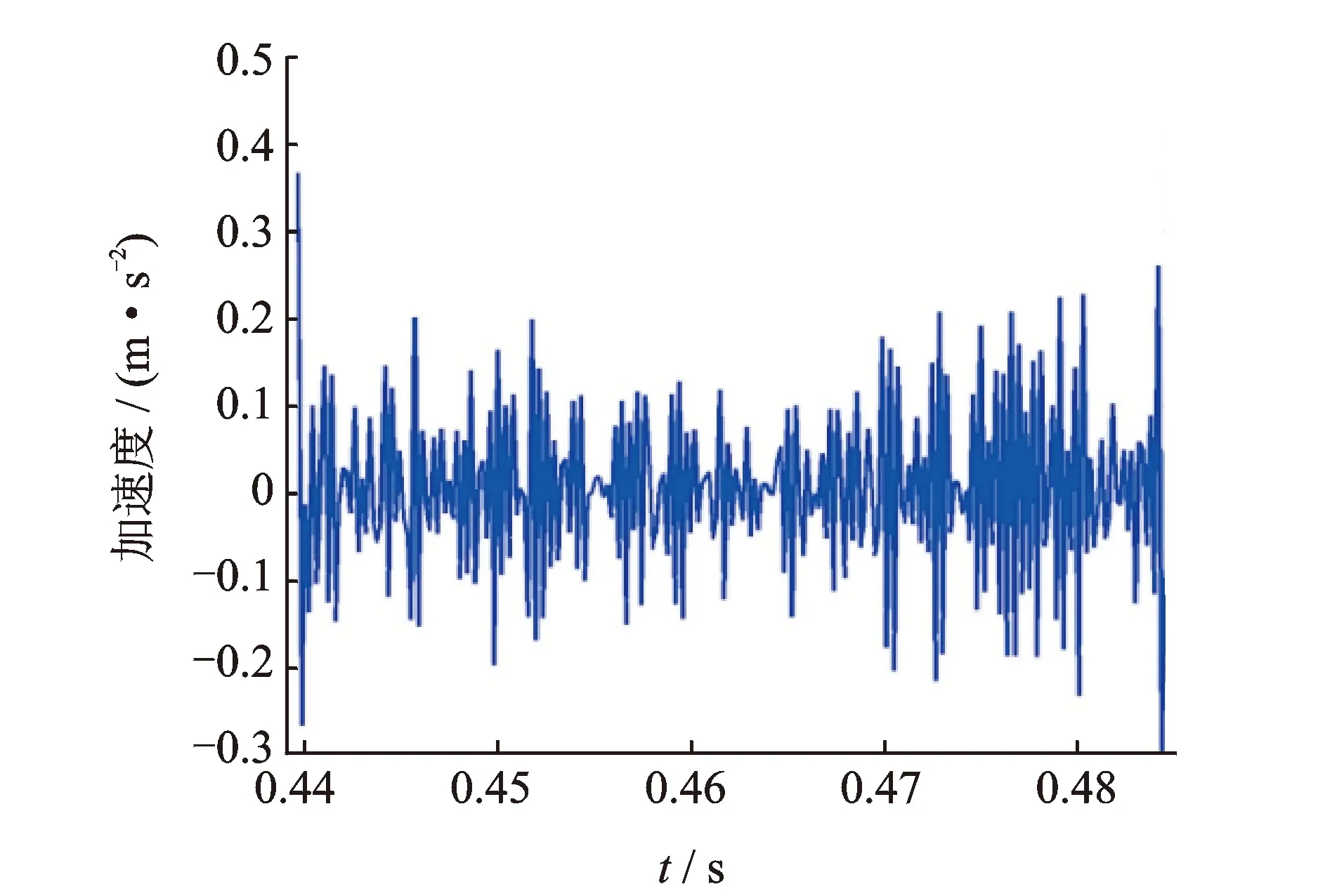
图7 飞切过程振动信号Fig.7 Vibration of fly cutting process
由图7可知,刀具在工件表面切削的时间仅为0.045 1 s。图8为飞切过程振动信号的频谱图。对比图8和表2可知,飞切轨迹波纹误差是切削过程中的部分振动作用在加工表面的结果。
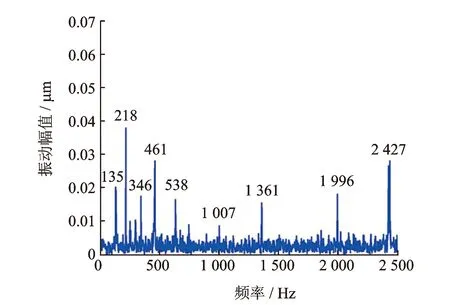
图8 切削振动信号频谱Fig.8 Frequency spectrum of fly cutting vibration
3.2 机床气浮主轴固有频率测试
为了进一步分析飞切轨迹波纹误差的来源,笔者对图5所示机床的气浮主轴下端面进行了锤击模态实验[10](见图9),获得主轴的前8阶固有频率分别为:133,254,345,461,538,818,1 004,1 364 Hz。

图9 机床气浮主轴锤击模态实验Fig.9 Experimental modal by ha mmering method for air spindle in the machine
3.3 飞切轨迹波纹误差频率成分辨识
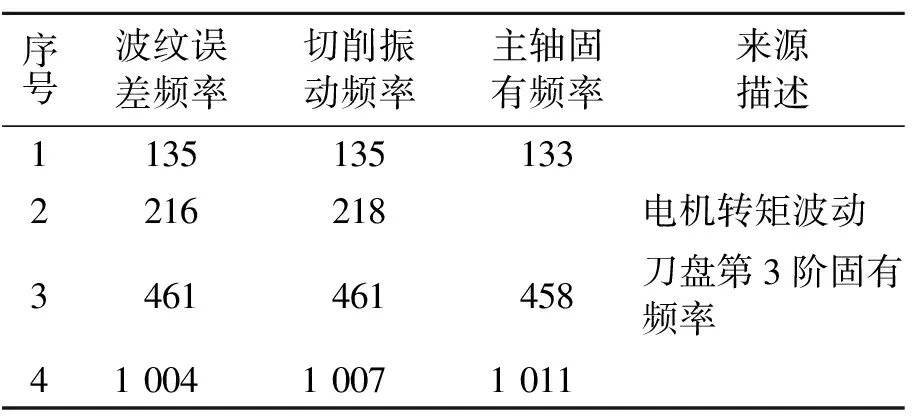
在完成飞切轨迹波纹误差频率成分分离、切削振动频率计算、机床气浮主轴固有频率测试后,表3所示为三者之间的对应关系。
由表3可知,飞切轨迹波纹误差与切削过程的振动以及主轴系统的动力学特性密切相关。飞切轨迹波纹误差是部分切削振动频率复印在工件表面上产生的,其中主轴系统在断续切削力的作用下按1,4,7阶固有频率产生的自激振动均在飞切轨迹轮廓上产生了波纹误差。频率为216 Hz的轨迹波纹误差通过振动测量实验发现其来自于主轴系统的驱动机构。
表3 飞切轨迹波纹误差频率辨识
Tab.3 Frequency indentification of waveness error at fly cutting trajectory Hz
4 KDP晶体飞切波纹误差实验
基于上述飞切轨迹波纹误差频率辨识结果,即轨迹波纹误差主要来源于主轴系统的固有频率和驱动机构。因此,在图5所示机床上对主轴系统重点进行了结构和驱动的优化改进:a.将主轴系统的刀盘结构与材料改进为整体轮辐式结构,在质量基本不变的情况下,刀盘第3阶固有频率提高至538 Hz。b.在主轴转子与驱动电机之间采用柔性拨叉驱动机构,消除电机转矩波动带来的冲击。在相同的飞切工艺参数下(切削深度3 μm,主轴转速265 r/min,进给速度2 mm/min,环境温度20±0.5 ℃),优化前后PSD1频段内KDP晶体金刚石飞切表面轮廓如图10所示。

图10 KDP晶体飞切PSD1表面轮廓Fig.10 Profile of the PSD1 surface by fly cutting for KDP crystals
由图10可知,优化后PSD1频段内KDP晶体飞切表面波纹误差RMS值从53 nm降低至12 nm,得到了有效的抑制。从而验证了飞切轨迹波纹误差频率辨识结果的准确性。
5 结束语
笔者提出了一种基于空间频率变换的飞切轨迹波纹误差分离方法。该方法避免了进给方向波纹误差的干扰,实现了波纹误差频率成分的准确分离。通过对比波纹误差频率、切削振动频率、主轴固有频率完成了飞切轨迹波纹误差的辨识。切削振动是导致飞切轨迹波纹误差的直接原因,其中主轴在断续切削力作用下随固有频率的自激振动及电机驱动导致的受迫振动是误差的主要来源。根据飞切轨迹波纹误差的辨识结果,重点对机床的主轴系统进行了结构和驱动的优化。优化后KDP晶体飞切表面PSD1频段内的RMS值得到了有效抑制。
[1] Goel S, Luo X C, Reuben R L.Molecular dynamics simulation model for the quantitative assessment of tool wear during single point diamond turning of cubic silicon carbide[J].Computational Materials Science,2012, 51(1):202-208.
[2] Wang Hongxiang,Zong Wenjun,Sun Tao, et al.Modification of three dimensional topography of the machined KDP crystal surface using wavelet analysismethod[J]. Applied Surface Science, 2010, 256(16): 5061-5068.
[3] Li L, Collins S A, Allen J, et al. Optical effects of surface finish by ultraprecision single point diamond machining [J]. Journal of Manufacturing Science and Engineering, 2010, 132 (2): 10021-10029.
[4] ISO/DTS 16610-32. Geometrical product specification (GPS)-filtration-part32: robust profile filters: spline filters[S]. British Standards Institution:International Organization for Standardization,2002.
[5] Lou Shan, Jiang Xiangqian, Scott P J. Correlating motif analysis and morphological filters for surface texture analysis[J].Measurement, 2013, 46(2): 993-1001.
[6] Zhang S J,To S,Cheung C F C F, et al. Dynamic characteristics of anaerostatic bearing spindle and its influence on surface topography inultra-precision diamond turning[J]. International Journal of Machine Tools and Manufacture,2012, 62(12): 1-12.
[7] 陈东菊,范晋伟,李海涌,等.超精密加工中表面波纹度与主轴系统不平衡关系[J].机械工程学报,2013,49(1):191-198.
Chen Dongju, Fan Jinwei, Li Haiyong,et al.Relationship between waviness in ultra-precision machining and spindle unbalance[J].Journal of Machanical Engineering,2013,49(1):191-198.(in Chinese)
[8] 程灏波.基于空间频率评价磁流变抛光非球面中频误差[J].哈尔滨工业大学学报,2006,38(6):917-919.
Chen Haobo. Error-regulating method for magnetorheological finished aspherics focused on spatial frequency[J]. Journal of Harbing Institute of Technology, 2006,38 (6):917-919.(in Chinese)
[9] Tan Qiaofeng, He Qingsheng, Yan Yingbai. Spatial-frequency spectrum analysis of the performanceof diffractive optical element for beam smoothing [J] International Journal for Light and Electron Optics,2002,113(4):163- 166.
[10]郑龙席,刘钢旗,梅庆,等.转子系统模态阻尼测定的相位匹配法[J].振动、测试与诊断,2014,34(2):218-222.
Zheng Longxi, Liu Gangqi,Mei Qing,et al. Research of measuring rotating mechanicla modal damping by phase mathcing method[J]. Journal of Vibration, Measurement & Diagnosis,2014,34(2):218 -222.(in Chinese)

*国家自然科学基金资助项目(51305413);中物院科技专项资助项目(9120602);四川省科技支撑计划资助项目(16ZC1083);四川省科技创新苗子工程资助项目(2016RZ0047)
2015-02-12;
2015-05-06
10.16450/j.cnki.issn.1004-6801.2017.02.004
TH69
阳红,男,1985年1月生,博士、工程师。主要研究方向为超精密金刚石切削工艺与装备。曾发表《基于热误差神经网络预测模型的机床重点热刚度辨识方法研究》(《机械工程学报》2011年第47卷第7期)等论文。
E-mail:oyanghongscu@163.com

