基于Sobel和hough变换的车道线识别算法研究

吴志军+洪顺利+王宝军

摘要：车道线的识别是车道保持系统的核心部分。文中提出了基于Sobel和hough变换的车道线识别算法，主要包括感兴趣区域设定、二维小波包分解降噪、Sobel算子的边缘检测和hough变换的车道线特征点识别。运用该算法对某一汽车常用工况下的车道线图像进行识别，试验结果表明该算法能较好地识别车道线。

关键词： 车道线；感兴趣区域；小波包分解；Sobel；hough变换

中图分类号：TP18 文献标识码：A 文章编号：1009-3044（2017）06-0214-03

Abstract：The identification of the lane mark is the core part of the lane keeping system. The lane line identification algorithm based on Sobel and hough transform is proposed in this paper. The algorithm mainly includes the setting of the region of interest， noise reduction on the application of the two-dimensional wavelet packet decomposition， the edge detection on the application of Sobel operator and the identification of lane line feature on the application of hough transform. The algorithm is used to identify the lane in an image which is under a common operating condition of a vehicle. The experimental results show that the algorithm can well identify the lane.

Key words：lane line；region of interest；wavelet packet decomposition；Sobel；hough transform.

1 概述

作為汽车主动安全系统之一的车道保持系统在汽车主动安全领域扮演的角色越来越重要。研究表明，大约15%的道路交通事故是由车辆驶离公路造成的[1]，车道保持系统能够有效地减少道路交通事故的发生。目前，关于车道保持系统的研究主要集中在两个方面：一是当检测到车辆在行驶过程中偏离车道时，系统向驾驶员发出车道偏离警告信号[2-5]；二是系统发送警告信号的同时，通过干预转向系统，纠正车辆姿态，使车辆行驶在正确的车道上，从而保证驾驶员的行车安全[6-10]。不管系统是否带有干预功能，车道线的识别是车道保持系统的核心部分，其识别质量的好坏直接影响着整个系统控制结果。本文提出了基于Sobel和hough变换的车道线识别算法，并通过某一汽车常用工况下对车道线图像进行识别试验，验证了算法的可行性和较好的识别效果。

2 车道线识别算法

整个车道线识别过程主要分为4部分：感兴趣区域设定、图像预处理、车道线边缘检测和车道线特征点识别，如图1所示。

2.1 感兴趣区域设定

为提高车道线识别的实时性和鲁棒性，降低车道线检测过程中的计算强度，提高车道偏移判定的准确率，同时提升系统的响应速度，在车道线识别之初，在图像中设定感兴趣区域（Region of Interest，简称ROI）。

结合车道线在车辆正常行驶或驶离原车道时在图像中可能的位置，本文设定了若干个边界条件，f1（x）、f2（x）、f3（x）、f4（x）、f5（x）以及图像自身边界。由此若干个边界围成的区域，如图2所示，即为感兴趣区域。本文采用的边界条件如下，以极坐标的形式表示：

2.2 图像预处理

图像在采集、获取、传送和转换过程中通常会受到随机信号的干扰，大量噪声产生会导致图像的质量下降，同时也会掩盖重要的图像信息，对图像的最终处理效果造成较大不良影响，故在对图像中的车道线进行识别前，还需对图像进行预处理——降噪。

本文采用二维小波包分解技术进行滤波降噪[11-12]。利用该技术能将频带进行多层次划分，对分辨率分析没有细分的高频部分进一步分解，且能依据被分析特征自适应地选择相应的频带，使之与信号频谱向匹配，从而提高时频分辨率。具体步骤如下：

1）对图像进行小波包分解。选取合适的小波并确定一个小波分解的层次N，接着对图像进行N层小波包分解；

2）计算最佳树，即确定最佳小波包基。在对图像进行小波包分解时，可采用多种小波包基，而通常根据分析图像的要求，从中选择最好的一种小波包基，即最优基；

3）对小波包分解系数的阈值进行量化；

4）对图像的小波包进行重构。根据第N层的小波包分解系数和量化处理系数，进行图像的小波包重构。

2.3 车道线边缘检测

本文采用Sobel算子的检测边缘方法[13-14]。Sobel算子从相异的方向检测图像，是一组方向算子，它并非简单的求均值在进行差分，而是提高了中心像素领域4个方向像素的权重。其计算式子如下：

式中，f（x，y）是图像坐标为（x，y）的整数像素灰度值，Sx和Sy分别是水平和垂直方向的一阶微分，S[f（x，y）]是Sobel算子的梯度。

2.4 车道线特征点识别

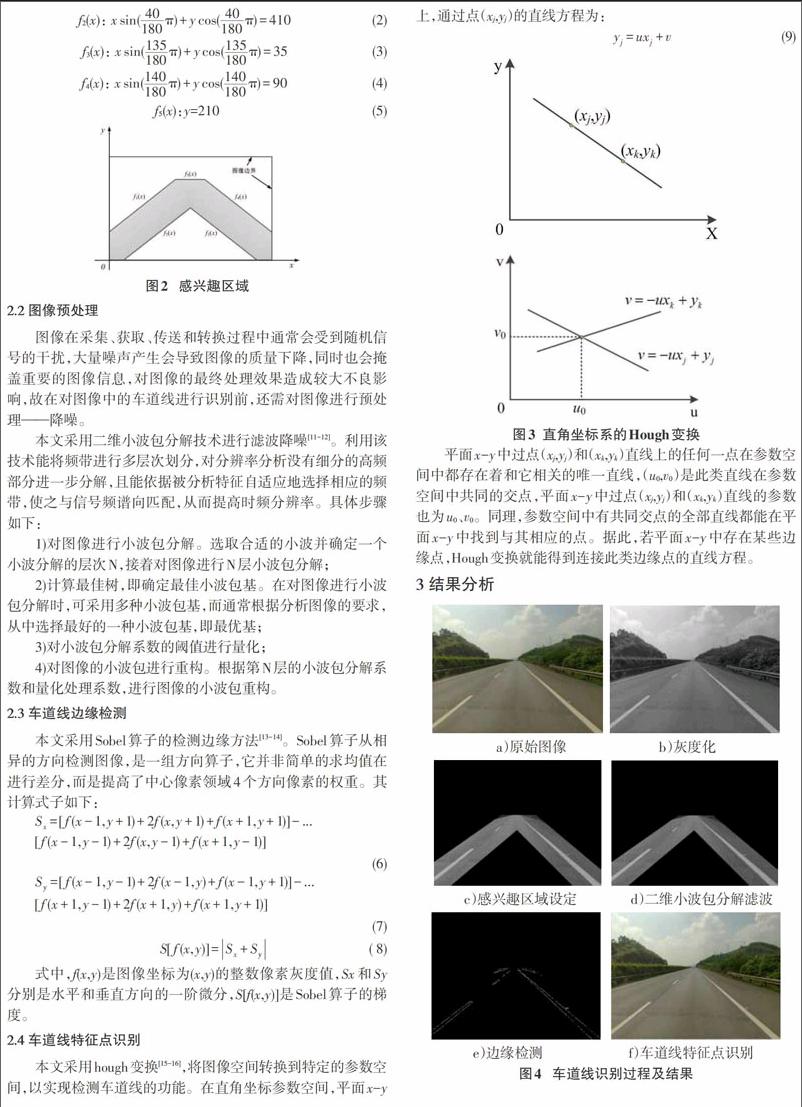
本文采用hough变换[15-16]，将图像空间转换到特定的参数空间，以实现检测车道线的功能。在直角坐标参数空间，平面x-y上，通过点（xj，yj）的直线方程为：

平面x-y中过点（xj，yj）和（xk，yk）直线上的任何一点在参数空间中都存在着和它相关的唯一直线，（u0，v0）是此类直线在参数空间中共同的交点，平面x-y中过点（xj，yj）和（xk，yk）直线的参数也为u0、v0。同理，参数空间中有共同交点的全部直线都能在平面x-y中找到与其相应的点。据此，若平面x-y中存在某些边缘点，Hough变换就能得到连接此类边缘点的直线方程。

3 结果分析

本文选取某段高速公路的车道线图像，尺寸为640×480，如图4（a）。为了降低运算量，提高运算速率，笔者将原始彩色图像进行了灰度化处理，如图4（b）。图4（c-f）显示的是车道线识别过程和结果。

二维小波包分解滤波后的图像滤除了原始图像中路面部分的椒盐噪声，车道线边缘特征点能较好地保留，但是相比原始图像，毛刺感要稍微强些。由于感兴趣区域设定时，除道路信息外还有部分环境信息未剔除，因此，边缘检测结果不仅包含车道线信息，还包括少部分其他物体的边缘信息，但车道线的边缘检测结果较好，特征点基本都被检测出来。车道线特征点识别效果较好，右侧连续车道线的识别结果与实际情况基本吻合，左侧不连续车道线的识别结果与实际情况虽有微小差距，但并不影响识别效果。

4 结论

本文针对车道保持系统的核心部分，提出了完整的车道线识别算法，包括设定感兴趣区域、二维小波包分解降噪、边缘检测和车道线特征点识别。通过对某段高速公路图像进行车道线识别，验证了算法的可行性。从试验结果可得，本文提出的车道线识别算法能较好地识别车道线，为车道保持系统的进一步设计奠定基础。

参考文献：

[1] NHTSA's national center for statistics & analysis. Traffic safety facts 2007[R]. National Highway Traffic Safety Administration，2008.

[2] 林广宇， 魏朗， 蹇小平.基于嵌入式的车辆偏离预警系统研究[J].电子设计工程，2010，18（8）：26-28.

[3] 秦洪懋.基于驾驶行为的车道偏离预警系统关键技术研究[D].镇江：江苏大学，2014.

[4] 陈普. 基于计算机视觉的车道偏离预警算法研究[D]. 南昌：南昌航空大学， 2015.

[5]余小角， 陈贤富. 基于视频的高速车道偏离预警系统[J]. 微型机与应用， 2016， 35（19）：21-24.

[6] 张海林.基于电动转向的车道保持系统[D].北京：清华大学，2012.

[7]张海林， 罗禹贡， 江青云，等. 基于电动助力转向的车道保持系统[J]. 汽车工程， 2013， 35（6）：526-531.

[8] 孔悦.基于虚拟行驶环境下的汽车车道保持技术研究[D].长春：吉林大学，2015.

[9] 孙涛， 徐正进， 郑松林，等. 基于电动助力转向的车道保持性能研究与分析[J]. 系统仿真学报， 2015， 27（12）：2913-2919.

[10] 柳长春， 都东， 潘际銮. 基于小偏差模型预测的车道保持辅助控制[J]. 清华大学学报：自然科学版， 2015（10）：1087-1092.

[11] 杨永明， 路陈红. 小波包分析在一维及二维信号去噪中的应用[J].西安建筑科技大学学报：自然科学版，2004，36（3）：364-367.

[12] 杨全海. 二维小波包分解在计算机图像重构中的应用[J]. 电子设计工程， 2016， 24（24）：173-175.

[13] 魏伟波， 芮筱亭.图像边缘检测方法研究[J].计算机工程与应用，2006，42（30）：88-91.

[14] 李正明， 刘春国， 安明建. 基于FPGA的Sobel图像边缘检测的设计[J]. 现代科学仪器， 2012（4）：88-90.

[15] 段大高，王建勇.圖像处理与应用[M].北京：北京邮电大学出版社，2013.

[16] 余厚云， 张为公， YuHouyun，等. 直线模型下的车道线跟踪与车道偏离检测[J]. 自动化仪表， 2009， 30（11）：1-3.